Baccalauréat STI2D et STL/SPCL - Polynésie 21 juin 2018 - Correction Exercice 1

Page 2 sur 8: Correction Exercice 1

Correction de l'exercice 1 (4 points)

QCM

Cet exercice est composé de deux parties indépendantes.

Partie A

Pour chacune des questions suivantes, une seule réponse est correcte.
Recopier sur la copie le numéro de la question et la lettre correspondant à la réponse choisie.
Aucune justification n'est demandée.
Une bonne réponse rapporte $0,5$ point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse ne rapportent ni n'enlèvent aucun point.

1. On donne ci-dessous la représentation graphique $\mathcal{C}$ d'une fonction$f$ définie sur $]-\infty~;~1[ \cup ]1~;~+\infty[$.
   1. $\displaystyle\lim_{x \to +\infty} f(x)=1$
   2. $\displaystyle\lim_{\substack{x \to 1 \\ x < 1}} f(x)= -\infty$
   3. $\displaystyle\lim_{\substack{x \to 1 \\ x > 1}} f(x)= -\infty$
   4. $\displaystyle\lim_{x\to -\infty} f(x)= -\infty$
   
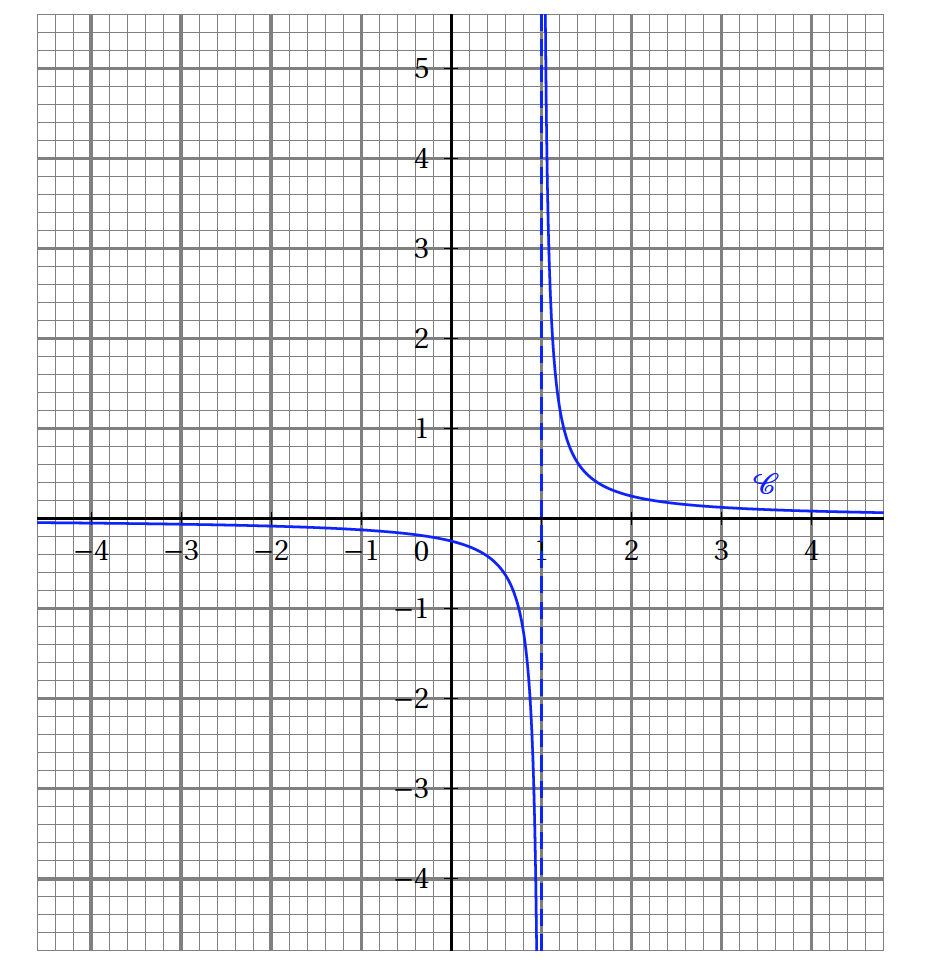Par lecture graphique, on a : $\displaystyle\lim_{\substack{x \to 1 \\ x < 1}} f(x)= -\infty$
2. Une solution $g$ de l'équation différentielle $y''+9y=0$ vérifiant $g(0)=1$ est définie sur $\mathbb R$ par:
   1. $g(t)= \cos\left (9t\right ) + \sin \left (9t\right )$
   2. $g(t)= 4\,\cos \left (3t\right ) - 3$
   3. $g(t)= \cos\left (3t\right ) + \sin \left (3t\right )$
   4. $g(t)= 2\, \cos\left (3t\right ) - \sin \left (3t\right )$
L'équation différentielle $y″+9⁢y=0$ est du type $y"+\omega ^2y=0$ où $\omega=3$.
Les solutions de l'équation différentielle $y″+9⁢y=0$ sont les fonctions définies $f$ sur $\mathbb R$ par $f(t)=A\cos\left (3t\right ) +B \sin \left (3t\right )$ où $A$ et $B$ sont deux constantes réelles.
La condition $g(0)=1$ équivaut à $A=1$.
Ainsi, une solution $g$ de cette l'équation différentielle vérifiant $g(0)=1$ est définie sur $\mathbb R$ par $f(t)=\cos\left (3t\right ) + \sin \left (3t\right )$
3. L'équation $\ln\left (x-2\right ) = -2$ admet pour solution dans $\mathbb R$:
   1. $0$
   2. $2+\text{e}^{-2}$
   3. $2,14$
   4. $2-\text{e}^{2}$
$\ln⁡ x-2=-2\iff x-2=e^{-2}\iff x=2+e^{-2}$
La bonne réponse est b.
4. La dérivée de la fonction $h$ définie sur $\mathbb R$ par $h(x)=x\text{e}^{-2x}$ est la fonction $h'$ définie sur $\mathbb R$ par:
   1. $h'(x)=\text{e}^{-2x}$
   2. $h'(x)=-2\text{e}^{-2x}$
   3. $h'(x)=-2x\text{e}^{-2x}$
   4. $h'(x)=\left (1-2x\right )\text{e}^{-2x}$
$h$ est dérivable comme somme de deux fonctions dérivables. $h=u v ,$ d'où $f'=u'v+v'u $ avec pour tout réel $x$: $\left\{ \begin{array}{l} u(x)~ =x \\ v(x)~ = \text{e}^{-2x}\end{array}\right.$ ainsi : $\left\{ \begin{array}{l} u'(x)~ = 1 \\ v'(x)~ = -2\text{e}^{-2x}\end{array}\right.$ $$ \begin{array}{cl} h'(x)& =1\times \text{e}^{-2x}+\left (-2\text{e}^{-2x}\right )\times x\\ & = \text{e}^{-2x}-2x\text{e}^{-2x} \\ &= \text{e}^{-2x}\left (1-2x\right ) \end{array} $$ La bonne réponse est d.

Partie B

Le plan complexe est muni d'un repère orthonormé $\left(\text{O}~;~\vec{u},~\vec{v}\right)$. On note $ \text{i}$ le nombre complexe de module 1 et d'argument $\dfrac{\pi}{2}$. On considère les points A, B et C du plan complexe d'affixes respectives $z_{\mathrm A}$, $z_{\mathrm B}$ et $z_{\mathrm C}$: \[z_{\mathrm A} = \dfrac{\sqrt{2} + \text{i} \sqrt{2}}{ \text{i}} \hspace{2cm} z_{\mathrm B} = 2 \text{e}^{ \text{i} \frac{\pi}{3}} \hspace{2cm} z_{\mathrm C} = -2 \text{i}\text{e}^{- \text{i}\frac{\pi}{6}}\] Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse et justifier les réponses choisies.Toute trace de recherche, même incomplète ou non fructueuse, sera prise en compte dans l'évaluation.
Une réponse non justifiée ne rapporte aucun point.

• Affirmation 1: La forme algébrique de $z_{\mathrm{A}}$ est $\sqrt{2}- \text{i}\sqrt{2}$.
$$ \begin{array}{cl} z_{\mathrm A} &= \dfrac{\sqrt{2} + \text{i} \sqrt{2}}{ \text{i}} \\ & = \dfrac{\left ( \sqrt{2} + \text{i} \sqrt{2} \right )\times ( -\text{i} )}{ \text{i}\times (- \text{i} )} \\ &= \dfrac{\left ( -\text{i}\sqrt{2} - \text{i} ^2\sqrt{2} \right )}{ 1} \\ &=\sqrt{2}-\text{i}\sqrt{2} \end{array} $$ L'affirmation 1 est donc vraie.
• Affirmation 2: Un argument de $z_{\mathrm{C}}$ est $\dfrac{\pi}{6}$.
$-2\text{i}\text{e}^{- \text{i}\frac{\pi}{6}}$ n'est pas une forme exponentielle d'un nombre complexe. Comme $\text{e}^{- \text{i}\frac{\pi}{2}}=- \text{i}$, on en déduit : $$ \begin{array}{cl} z_{\mathrm C} &= -2\text{i}\text{e}^{- \text{i}\frac{\pi}{6}} \\ & = 2 \text{e}^{- \text{i}\frac{\pi}{2}} \text{e}^{- \text{i}\frac{\pi}{6}} \\ &= 2 \text{e}^{- \text{i}(-\frac{\pi}{2}-\frac{\pi}{6})} \\ &2 \text{e}^{- \text{i} \frac{2\pi}{3} } \end{array} $$ L'affirmation 2 est fausse : un argument de $z_{\mathrm C}$ est $-\frac{2\pi}{3}$.
• Affirmation 3: Les points A, B et C sont sur un même cercle de centre O.
Le module du nombre complexe $z_{\mathrm A}=\sqrt 2-\text{i}\sqrt ⁢2$ est : $\rvert z_{\mathrm A}\rvert=\sqrt{\sqrt ⁢2^2+\sqrt ⁢2^2}=\sqrt 4=2$.
Le module du nombre complexe $z_{\mathrm B}=2⁢\text{e}^{ \text{i}\frac{\pi}{3}} $ est $\rvert z_{\mathrm B}\rvert =2$ et, le module du nombre complexe $z_{\mathrm C}= 2 \text{e}^{- \text{i}( \frac{2\pi}{3}}$ est $\rvert z_{\mathrm C}\rvert =2$
L'affirmation 3 est vraie : $\rvert z_{\mathrm A}\rvert = \rvert z_{\mathrm B}\rvert =\rvert z_{\mathrm C}\rvert =2$ donc les points A, B et C sont sur le cercle de centre O et de rayon 2.
• Affirmation 4: O est le milieu du segment [BC].
$$ \begin{array}{cl} \left (\vec{OC} ;\vec{OB}\right )&=arg\left (\dfrac{z_{\mathrm B}}{z_{\mathrm C}}\right ) \\ &= arg\left( z_{\mathrm B} \right ) -arg\left ( z_{\mathrm C} \right ) \\ & =\frac{\pi}{3} -\left ( -\frac{2\pi}{3} \right )\\ &=\pi\\ \end{array} $$ Comme $\left (\vec{OC} ;\vec{OB}\right )=\pi$, les vecteurs $\vec{OC}$ et $\vec{OB}$ sont colinéaires de sens opposé.
Par ailleurs $\rvert z_{\mathrm B}\rvert =\rvert z_{\mathrm C}\rvert =2$, donc $OB=OC=2$.
L'affirmation 4 est vraie :O est le milieu du segment [BC].