Baccalauréat STI2D Antilles-Guyane - 19 juin 2019 - Correction Exercice 3
Page 6 sur 8
Correction de l'exercice 3 (6 points)
- En raison des frottements avec l'atmosphère résiduelle terrestre, les satellites en orbite basse perdent progressivement de l'altitude et finissent par se consumer dans les couches les plus denses de l'atmosphère. Cet événement est appelé rentrée atmosphérique. Le temps, exprimé en jour, avant la rentrée atmosphérique dépend des caractéristiques du satellite et de l'altitude $h$, exprimée en kilomètre, de son orbite. Pour un satellite donné, ce temps est modélisé par une fonction $T$ de la variable $h$, définie et dérivable sur l'intervalle $[0~;~+\infty [$.
Les trois parties de cet exercice peuvent être traitées de manière indépendante.
Partie A – Étude d'un premier satellite
- Résoudre l'équation différentielle $(E)$ sur $[0~;~+\infty [$. Les solutions de l'équation différentielle $y′=ay+b$ sont les fonctions définies sur $\mathbb R$ par $x\mapsto k\text{e}^{ax}+\dfrac{b}{a}$, où $k$ est une constante réelle quelconque.
- Déterminer la fonction $T$ solution de l'équation différentielle $(E)$ qui vérifie la condition $T(800)= 2000 $. $T(800)= 2000 \iff k\text{e}^{0,025 \times 800}=2000\iff k=2000\text{e}^{-20}$
- On admet que la fonction $T$, associée à ce premier satellite, est une solution de l'équation différentielle $(E)$ suivante dans laquelle $y$ désigne une fonction de la variable $h$ définie et dérivable sur $[0~;~+\infty [$ et $y'$ la fonction dérivée de $y$.\[(E)\;:\;40y'-y = 0.\]
Or $40y′-y=0\iff y′=0,025\times y$
Par conséquent, les solutions de l'équation différentielle (E) sont les fonctions définies sur $[0~;~+\infty [$ par $T(h)=k\text{e}^{0,025 h}$ où $k$ est une constante réelle quelconque.
La solution de l'équation différentielle (E) qui vérifie la condition $T(800)= 2000 $ est la fonction définie sur $[0~;~+\infty [$ par $T(h)=k\text{e}^{0,025 h-20}$.
Partie B– Étude d'un deuxième satellite
- Dans cette partie, on admet que la fonction $T$, associée à ce deuxième satellite, est définie sur l'intervalle $[0~;~+\infty[$ par : \[T(h) = K\times0,012\text{e}^{0,025(h-150)}.\] Le nombre réel $K$ est appelé coefficient balistique du satellite. La fonction $T$ associée à ce deuxième satellite est représentée ci-après.
Dans cette partie, on ne demande pas de justification. Les résultats seront donnés avec la précision permise par le graphique.
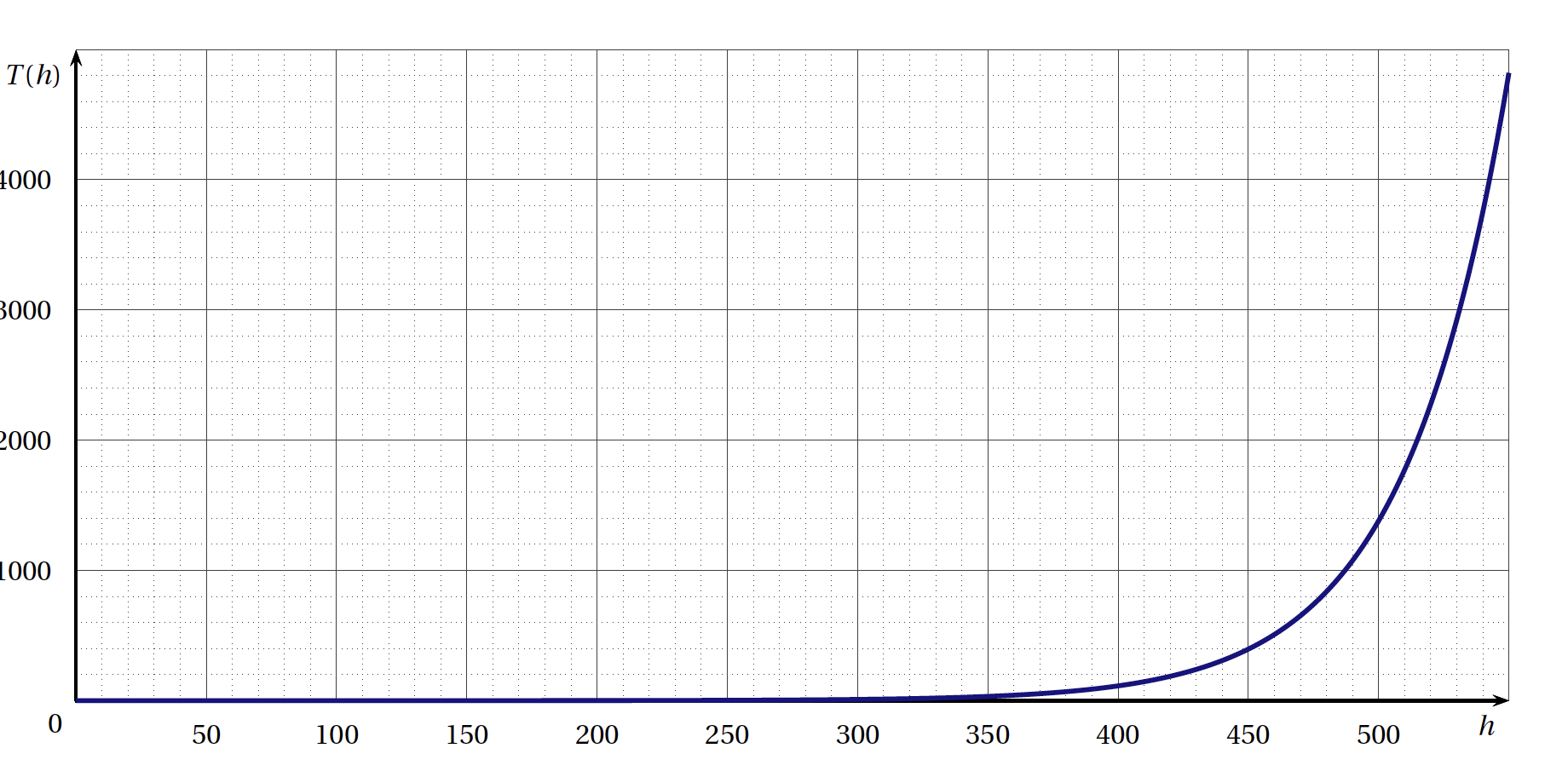
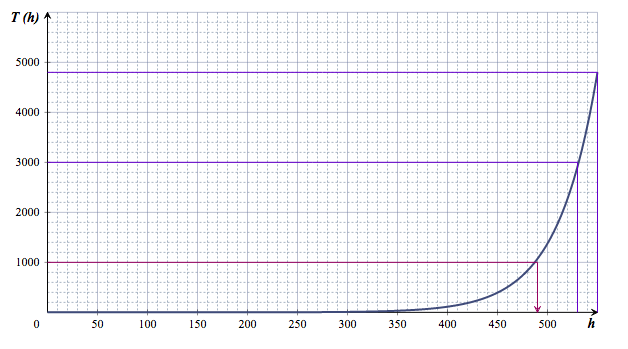
- À quelle altitude minimale faut-il mettre en orbite ce deuxième satellite pour que le temps restant avant sa rentrée atmosphérique soit au moins égal à 1000 jours ? Avec la précision permise par le graphique, $T(h)\geq 1000$ pour $h\geq490$.
- Déterminer une valeur approchée du coefficient balistique $K$ de ce deuxième satellite. Avec la précision permise par le graphique, plusieurs valeurs sont possibles. Par exemple :
- Avec $T(530)=3000$. Une valeur approchée de $K$ est solution de l'équation : $$\begin{array}{rl} T(530)=3000& \iff K\times0,012\text{e}^{0,025(530-150)} =3000\\ & \iff K\times0,012\text{e}^{9,5} =3000 \\ &\iff K= \dfrac{3000}{0,012\text{e}^{9,5}}\\ &\text{Soit } K\approx 18,7 \end{array}$$
- Avec $T(550)=4800$. Une valeur approchée de $K$ est solution de l'équation : $$\begin{array}{rl} T(550)=4800& \iff K\times0,012\text{e}^{0,025(550-150)} =4800\\ & \iff K\times0,012\text{e}^{10} =4800 \\ &\iff K= \dfrac{3000}{0,012\text{e}^{10}}\\ &\text{Soit } K\approx 18,2 \end{array}$$
Pour que le temps restant avant sa rentrée atmosphérique soit au moins égal à 1 000 jours il faut mettre ce deuxième satellite à une altitude supérieure à 490 km.
Partie C – Étude d'un troisième satellite : Hubble
- L'orbite du satellite Hubble est située à l'altitude $h$ de 575 km. Calculer le temps $T(h)$ restant avant la rentrée atmosphérique du satellite Hubble. Arrondir au jour près. $$T(575)=0,0132\text{e}^{0,025\times 425}\approx 5432$$ Le temps restant avant la rentrée atmosphérique du satellite Hubble est d'environ 5 432 jours.
- Déterminer la limite de $T$ en $+\infty$. $\lim\limits_{h\to +\infty} =0,0255\times(h-150) =+\infty $ d'où $\lim\limits_{h\to +\infty} \text{e}^{0,025(h-150)}= +\infty$ et donc $\lim\limits_{h\to +\infty} 0,132\text{e}^{0,025(h-150)}= +\infty $
-
- Déterminer $T'(h)$, où $T'$ désigne la fonction dérivée de $T$. $T $ est solution de l'équation différentielle (E) d'où $T'(h)=0,025\times T(h)$ soit $T'(h)=0,025\times 0,132\text{e}^{0,025(h-150)}=0,00033\text{e}^{0,025(h-150)}$
- En déduire le sens de variations de la fonction $T$ sur $[0~;~ +\infty [$. Pour tout réel $h, 3\text{e}^{0,025(h-150)}>0$ donc $0,00033\text{e}^{0,025(h-150)}> 0$.
$T'$ est la fonction définie sur l'intervalle $[0;+\infty[$ par :$T'(h)=0,00033\text{e}^{0,025(h-150)}$
$T'(h)> 0$ donc la fonction $T $ est strictement croissante sur $[0;+\infty[$. - On souhaite étudier l'effet d'une augmentation de 10 km de l'altitude $h$ sur le temps restant avant la rentrée atmosphérique du satellite Hubble.
- Montrer que $T(h + 10)= \text{e}^{0,25}\times T(h)$. Ainsi $T(h + 10)= \text{e}^{0,25}\times T(h)$.
- En déduire qu'augmenter l'altitude $h$ de 10 km revient à augmenter d'environ 28% le temps restant avant la rentrée atmosphérique du satellite Hubble. $ \text{e}^{0,025 }\approx 1,284$ d'où $T(h+10)\approx \left(1+\dfrac{28,4}{100}\right)\times T(h)$.
Ainsi, augmenter l'altitude $h$ de 10 km revient à augmenter d'environ 28 % le temps restant avant la rentrée atmosphérique du satellite Hubble.
- Le satellite Hubble a un coefficient balistique $K$ égal à 11. La fonction $T$, associée à ce troisième satellite, est donc définie sur l'intervalle $[0~;~ +\infty [$ par : \[T(h)=0,132\text{e}^{0,025(h-150)}.\]
Exercice 4
- Vues: 22600
