Baccalauréat S Antilles-Guyane 11 septembre 2013 - Exercice 2
Page 3 sur 10
Exercice 2 6 points
Pour tout réel $k$ strictement positif, on désigne par $f_{k}$ la fonction définie et dérivable sur l'ensemble des nombres réels $\mathbb{R}$ telle que :
\[f_{k}(x) = kx\text{e}^{-kx}.\] On note $\mathcal{C}_{k}$ sa courbe représentative dans le plan muni d'un repère orthogonal $\left(\text{O}, \vec{i}, \vec{j}\right)$.
Partie A : Étude du cas $k = 1$
On considère donc la fonction $f_{1}$ définie sur $\mathbb{R}$ par
\[f_{1}(x) = x\text{e}^{- x}.\]
- Déterminer les limites de la fonction $f_{1}$ en $- \infty$ et en $+ \infty$. En déduire que la courbe $\mathcal{C}_{1}$ admet une asymptote que l'on précisera.
- Étudier les variations de $f_{1}$ sur $\mathbb{R}$ puis dresser son tableau de variation sur $\mathbb{R}$.
- Démontrer que la fonction $g_{1}$ définie et dérivable sur $\mathbb{R}$ telle que : \[g_{1}(x) = - (x + 1)\text{e}^{- x}\] est une primitive de la fonction $f_{1}$ sur $\mathbb{R}$.
- Étudier le signe de $f_{1}(x)$ suivant les valeurs du nombre réel $x$.
- Calculer, en unité d'aire, l'aire de la partie du plan délimitée par la courbe $\mathcal{C}_{1}$, l'axe des abscisses et les droites d'équation $x = 0$ et $x = \ln 10$.
Partie B : Propriétés graphiques
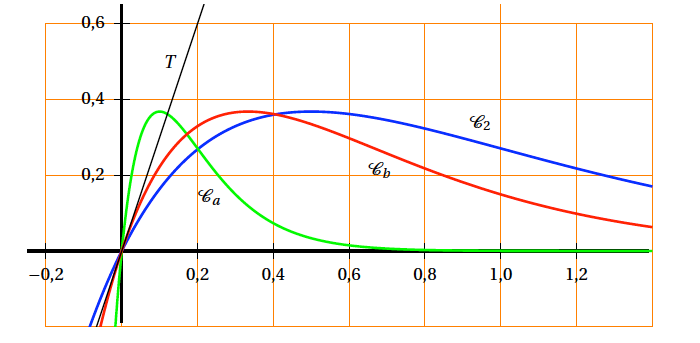
On a représenté sur le graphique ci-dessous les courbes $\mathcal{C}_{2}$, $\mathcal{C}_{a}$ et $\mathcal{C}_{b}$ où $a$ et $b$ sont des réels strictement positifs fixés et T la tangente à $\mathcal{C}_{b}$ au point O origine du repère.
- Montrer que pour tout réel $k$ strictement positif, les courbes $\mathcal{C}_{k}$ passent par un même point.
-
- Montrer que pour tout réel $k$ strictement positif et tout réel $x$ on a \[f'_{k}(x) = k(1 - kx)\text{e}^{- kx}.\]
- Justifier que, pour tout réel $k$ strictement positif, $f_{k}$ admet un maximum et calculer ce maximum.
- En observant le graphique ci-dessus, comparer $a$ et 2. Expliquer la démarche.
- Écrire une équation de la tangente à $\mathcal{C}_{k}$ au point O origine du repère.
- En déduire à l'aide du graphique une valeur approchée de $b$.
- Vues: 45412
