Baccalauréat S Amérique du Sud 21 novembre 2017

Page 1 sur 12

Exercice 1 6 points

Commun à tous les candidats

La chocolaterie Delmas décide de commercialiser de nouvelles confiseries : des palets au chocolat en forme de goutte d'eau. Pour cela, elle doit fabriquer des moules sur mesure qui doivent répondre à la contrainte suivante : pour que cette gamme de bonbons soit rentable, la chocolaterie doit pouvoir en fabriquer au moins $80$ avec $1$ litre de pâte liquide au chocolat.

Partie A : modélisation par une fonction

Le demi contour de la face supérieure du palet sera modélisé par une portion de la courbe de la fonction $f$ définie sur $]0~;~+ \infty[$ par : \[f(x) = \dfrac{x^2 - 2x - 2 - 3\ln x}{x}.\] La représentation graphique de la fonction $f$ est donnée ci-dessous.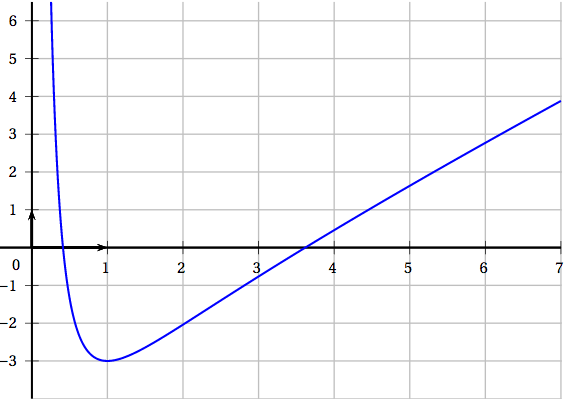

Le repère est orthogonal d'unité $2$ cm en abscisses et $1$ cm en ordonnées.

1. Soit $\varphi$ la fonction définie sur $]0~;~+ \infty[$ par : \[\varphi(x) = x^2 - 1 + 3\ln x.\]
   1. Calculer $\varphi(1)$ et la limite de $\varphi$ en $0$.
   2. Étudier les variations de $\varphi$ sur $]0~;~+ \infty[$. En déduire le signe de $\varphi(x)$ selon les valeurs de $x$.
2. 1. Calculer les limites de $f$ aux bornes de son ensemble de définition.
   2. Montrer que sur $]0~;~+ \infty[$ : $f'(x) = \dfrac{\varphi(x)}{x^2}$. En déduire le tableau de variation de $f$.
   3. Prouver que l'équation $f(x) = 0$ admet une unique solution $\alpha$ sur $]0~;~1]$. Déterminer à la calculatrice une valeur approchée de $\alpha$ à $10^{-2}$ près. On admettra que l'équation $f(x) = 0$ a également une unique solution $\beta$ sur $[1~;~+ \infty[$ avec $\beta \approx 3,61$ à $10^{-2}$ près.
   4. Soit $F$ la fonction définie sur $]0~;~+ \infty[$ par : \[F(x) = \dfrac{1}{2}x^2 - 2x - 2\ln x - \dfrac{3}{2}(\ln x)^2.\] Montrer que $F$ est une primitive de $f$ sur $]0~;~+ \infty[$.

 

Partie B : résolution du problème

Dans cette partie, les calculs seront effectués avec les valeurs approchées à $10^{-2}$ près de $\alpha$ et $\beta$ de la partie .
Pour obtenir la forme de la goutte, on considère la courbe représentative $C$ de la fonction $f$ restreinte à l'intervalle $[\alpha~;~\beta]$ ainsi que son symétrique $C'$ par rapport à l'axe des abscisses. Les deux courbes $C$ et $C'$ délimitent la face supérieure du palet. Pour des raisons esthétiques, le chocolatier aimerait que ses palets aient une épaisseur de $0,5$ cm. Dans ces conditions, la contrainte de rentabilité serait-elle respectée ?