Baccalauréat Polynésie 11 septembre 2014 STI2D--STL spécialité SPCL

Page 1 sur 8

Exercice 1 4 points

Nombres complexes

On considère les nombres complexes $Z_{1}$ et $Z_{2}$ : \[Z_{1} = \dfrac{3\sqrt{2}}{1 + \text{i}}\quad \text{et}\quad Z_{2} = \dfrac{4\text{i}}{1 + \text{i}\sqrt{3}}.\]

1. Ecrire les nombres $Z_{1}$ et $Z_{2}$ sous forme algébrique et trigonométrique.
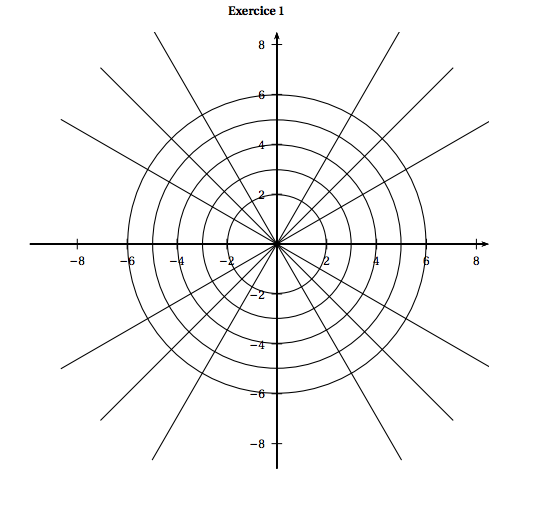
2. Placer les points A$_{1}$ et A$_{2}$ d'affixes respectives $Z_{1}$ et $Z_{2}$ dans le repère donné en annexe.
3. Calculer sous forme algébrique le produit $Z_{1} \times Z_{2}$ et donner sa forme trigonométrique.
4. En déduire les valeurs exactes de $\cos \dfrac{\pi}{12}$ et $\sin \dfrac{\pi}{12}$.