Baccalauréat S Métropole 21 juin 2019 - Exercice 4
Page 7 sur 10
Exercice 4 5 points
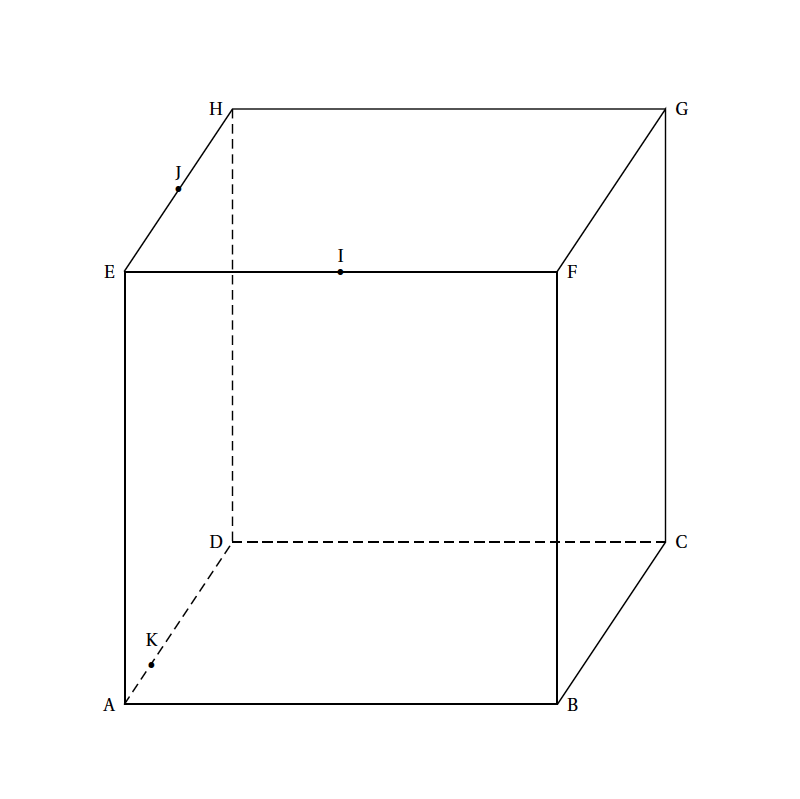
Les parties A et B peuvent être traitées de manière indépendante. On considère un cube ABCDEFGH d’arête de longueur 1, dont la figure est donnée en annexe.
On note I le milieu du segment [EF], J le milieu du segment [EH] et K le point du segment [AD] tel que $\vec{AK} = \frac{1}{4}\vec{AK}$.
On note $\mathscr{P}$ le plan passant par I et parallèle au plan (FHK).
Partie A
ans cette partie, les constructions demandées seront effectuées sans justification sur la figure donnée en annexe, à rendre avec la copie.
- Le plan $(FHK)$ coupe la droite $(AE)$ en un point qu’on note $M$. Construire le point $M$.
- Construire la section du cube par le plan $\mathscr{P}$.
Partie B
Dans cette partie, on munit l’espace du repère orthonormé $\left(A ; \vec{AB} ; \vec{AD} ; \vec{AE}\right)$.
On rappelle que $\mathscr{P}$ est le plan passant par $I$ et parallèle au plan $(FHK)$.
- Montrer que le vecteur $\vec{n}\begin{pmatrix} 4 \\ 4\\ -3\\ \end{pmatrix} $ est un vecteur normal au plan $(FHK)$.
- En déduire qu'une équation cartésienne du plan $(FHK)$ est : $4x + 4y - 3z - 1 = 0$.
- Déterminer une équation cartésienne du plan $\mathscr{P}$.
- Calculer les coordonnées du point $M$, point d’intersection du plan $\mathscr{P}$ et de la droite $(AE)$.
- On note $\Delta$ la droite passant par le point $E$ et orthogonale au plan $\mathscr{P}$.
- Déterminer une représentation paramétrique de la droite $\Delta$.
- Calculer les coordonnées du point $L$, intersection de la droite $\Delta$ et du plan $(ABC)$.
- Tracer la droite $\Delta$ sur la figure donnée en annexe, à rendre avec la copie.
- Les droites $\Delta$ et $(BF)$ sont-elles sécantes ? Qu'en est-il des droites $\Delta$ et $(CG)$ ? Justifier.
Annexe
- Vues: 64916
