Baccalauréat S Métropole 21 juin 2019 - Correction Exercice 4

Page 8 sur 10: Correction Exercice 4

Correction de l'exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Les parties A et B peuvent être traitées de manière indépendante. On considère un cube ABCDEFGH d’arête de longueur 1, dont la figure est donnée en annexe.
On note I le milieu du segment [EF], J le milieu du segment [EH] et K le point du segment [AD] tel que $\vec{AK} = \frac{1}{4}\vec{AK}$.
On note $\mathscr{P}$ le plan passant par I et parallèle au plan (FHK).

Partie A

ans cette partie, les constructions demandées seront effectuées sans justification sur la figure donnée en annexe, à rendre avec la copie.

1. Le plan $(FHK)$ coupe la droite $(AE)$ en un point qu’on note $M$. Construire le point $M$.
Les droites $(AE)$ et $(HK)$ sont incluses dans le plan $(EAH)$. Le point $M$ est donc le point d’intersection de ces deux droites.

 

Voir la figure à la fin de l’exercice.

 

$\quad$
1. Construire la section du cube par le plan $\mathscr{P}$.
D’après le théorème des milieux, appliqué dans le triangle $EFH$, les droites $(IJ)$ et $(FH)$ sont parallèles.

 

La droite $(FM)$ est l’intersection des plans $(AEF)$ et $(FHK)$.

 

L’intersection du plan $\mathscr{P}$ et de la face $ABFE$ est donc la droite parallèle à la droite $(FM)$ passant par le point $I$.

 

$\quad$

Partie B

Dans cette partie, on munit l’espace du repère orthonormé $\left(A ; \vec{AB} ; \vec{AD} ; \vec{AE}\right)$.
On rappelle que $\mathscr{P}$ est le plan passant par $I$ et parallèle au plan $(FHK)$.

1. 1. Montrer que le vecteur $\vec{n}\begin{pmatrix} 4 \\ 4\\ -3\\ \end{pmatrix} $ est un vecteur normal au plan $(FHK)$.
   Les coordonnées du point :
   
   
   – $F$ sont $(1;0;1)$
   
   
   – $H$ sont $(0;1;1)$
   
   
   – $K$ sont $(0;0,25;0)$.
   
   
   Ainsi $\vec{FH}(-1;1;0)$ et $\vec{FK}(-1;0,25;-1)$. Ces deux vecteurs ne sont clairement pas colinéaires.
   
   
   Donc $\vec{n}.\vec{FH}=-4+4+0=0$ et $\vec{n}.\vec{FK}=-4+1+3=0$.
   
   
   Le vecteur $\vec{n}$ est donc orthogonal à deux vecteurs non colinéaires du plan $(FHK)$.
   
   
   C’est un vecteur normal à ce plan.
   
   
   $\quad$
   
   
   1. En déduire qu'une équation cartésienne du plan $(FHK)$ est : $4x + 4y - 3z - 1 = 0$.
   Une équation cartésienne du plan $(FHK)$ est donc de la forme $4x+4y-3z+d=0$.
   
   
   Le point $F(1;0;1)$ appartient à ce plan donc $4+0-3+d=0\iff d=-1$.
   
   
   Une équation cartésienne du plan $(FHK)$ est dp,c $4x+4y-3z-1=0$.
   
   
   $\quad$
   
   
   1. Déterminer une équation cartésienne du plan $\mathscr{P}$.
   Les plans $\mathscr{P}$ et $(FHK)$ sont parallèles. Par conséquent, le vecteur $\vec{n}$ est aussi un vecteur normal au plan $\mathscr{P}$.
   
   
   Une équation cartésienne du plan $\mathscr{P}$ est donc de la forme $4x+4y-3z+d=0$.
   
   
   Le point $I$ a pour coordonnées $(0,5;0;1)$.
   
   
   Ainsi $2+0-3+d=0\iff d=1$.
   
   
   Une équation cartésienne du plan $\mathscr{P}$ est $4x+4y-3z+1=0$.
   
   
   $\quad$
   
   
   1. Calculer les coordonnées du point $M'$, point d’intersection du plan $\mathscr{P}$ et de la droite $(AE)$.
   On a $\vec{AE}(0;0;1)$.
   
   
   Une représentation paramétrique de la droite $(AE)$ est donc $\begin{cases} x=0\\y=0\\z=t\end{cases} \quad, t\in \mathbb R$.
   
   
   Les coordonnées du point d’intersection de la $(AE)$ et du plan $\mathscr{P}$ sont solutions du système :
   
   
   $\begin{cases} 4x+4y-3z+1=0 \\x=0\\y=0\\z=t\end{cases}\iff \begin{cases} -3t+1=0\\x=0\\y=0\\z=t\end{cases}\iff \begin{cases} t=\dfrac{1}{3}\\x=0\\y=0\\z=\dfrac{1}{3}\end{cases}$.
   
   
   Le point $M'$ a donc pour coordonnées $\left(0;0;\dfrac{1}{3}\right)$.
   
   
   $\quad$
2. On note $\Delta$ la droite passant par le point $E$ et orthogonale au plan $\mathscr{P}$.
   1. Déterminer une représentation paramétrique de la droite $\Delta$.
   Le vecteur $\vec{n}$ est donc un vecteur directeur de $\Delta$.
   
   
   Une représentation paramétrique de la droite $\Delta$ est : $$\begin{cases} x=4k\\y=4k\\z=1-3k\end{cases}\quad ,k\in \mathbb R$$
   
   
   $\quad$
   
   
   1. Calculer les coordonnées du point $L$, intersection de la droite $\Delta$ et du plan $(ABC)$.
   Une équation cartésienne du plan $(ABC)$ est $z=0$.
   
   
   Les coordonnées du point $L$ sont donc solution du système :
   
   
   $\begin{cases}z=0\\x=4k\\y=4k\\z=1-3k\end{cases}\iff\begin{cases}1-3k=0\\x=4k\\y=4k\\z=1-3k\end{cases}\iff \begin{cases} k=\dfrac{1}{3}\\x=\dfrac{4}{3}\\y=\dfrac{4}{3}\\z=0\end{cases}$.
   
   
   Donc $L$ a pour coordonnées $\left(\dfrac{4}{3};\dfrac{4}{3};0\right)$.
   
   
   $\quad$
   
   
   1. Tracer la droite $\Delta$ sur la figure donnée en annexe, à rendre avec la copie.
   Voir figure.
   
   
   $\quad$
   
   
   1. Les droites $\Delta$ et $(BF)$ sont-elles sécantes ? Qu'en est-il des droites $\Delta$ et $(CG)$ ? Justifier.
   $\quad$
   
   
   $\vec{BF}\begin{pmatrix} 0 \\ 0\\ 1\\ \end{pmatrix} $
   
   
   Une représentation paramétrique de la droite $(BF)$ est : $$\begin{cases} x=1\\y=0\\z=t\end{cases}\quad ,t\in \mathbb R$$
   
   
   $\quad$
   
   
   Pour déterminer l'intersection des droites $\Delta$ et $(BF)$, on résout le système :
   
   
   $\begin{cases}4k=1\\4k=0\\ 1-3k=t\end{cases}$.
   
   
   Ce système n'a pas de solution, donc les droites $\Delta$ et $(BF)$ ne sont pas sécantes
   
   
   $\vec{CG}\begin{pmatrix} 0 \\ 0\\ 1\\ \end{pmatrix} $
   
   
   Une représentation paramétrique de la droite $(CG)$ est : $$\begin{cases} x=1\\y=1\\z=t\end{cases}\quad ,t\in \mathbb R$$
   
   
   $\quad$
   
   
   Pour déterminer l'intersection des droites $\Delta$ et $(CG)$, on résout le système :
   
   
   $\begin{cases}4k=1\\4k=1\\ 1-3k=t\end{cases}\iff\begin{cases} k=\frac{1}{4}\\ t=\frac{1}{4} \end{cases} $.
   
   
   $t=\frac{1}{4}$ fournit le point $P(1;1;\frac{1}{4})$.
   
   
   Les droites $\Delta$ et $(CG)$ sont sécantes en $P(1;1;\frac{1}{4})$.

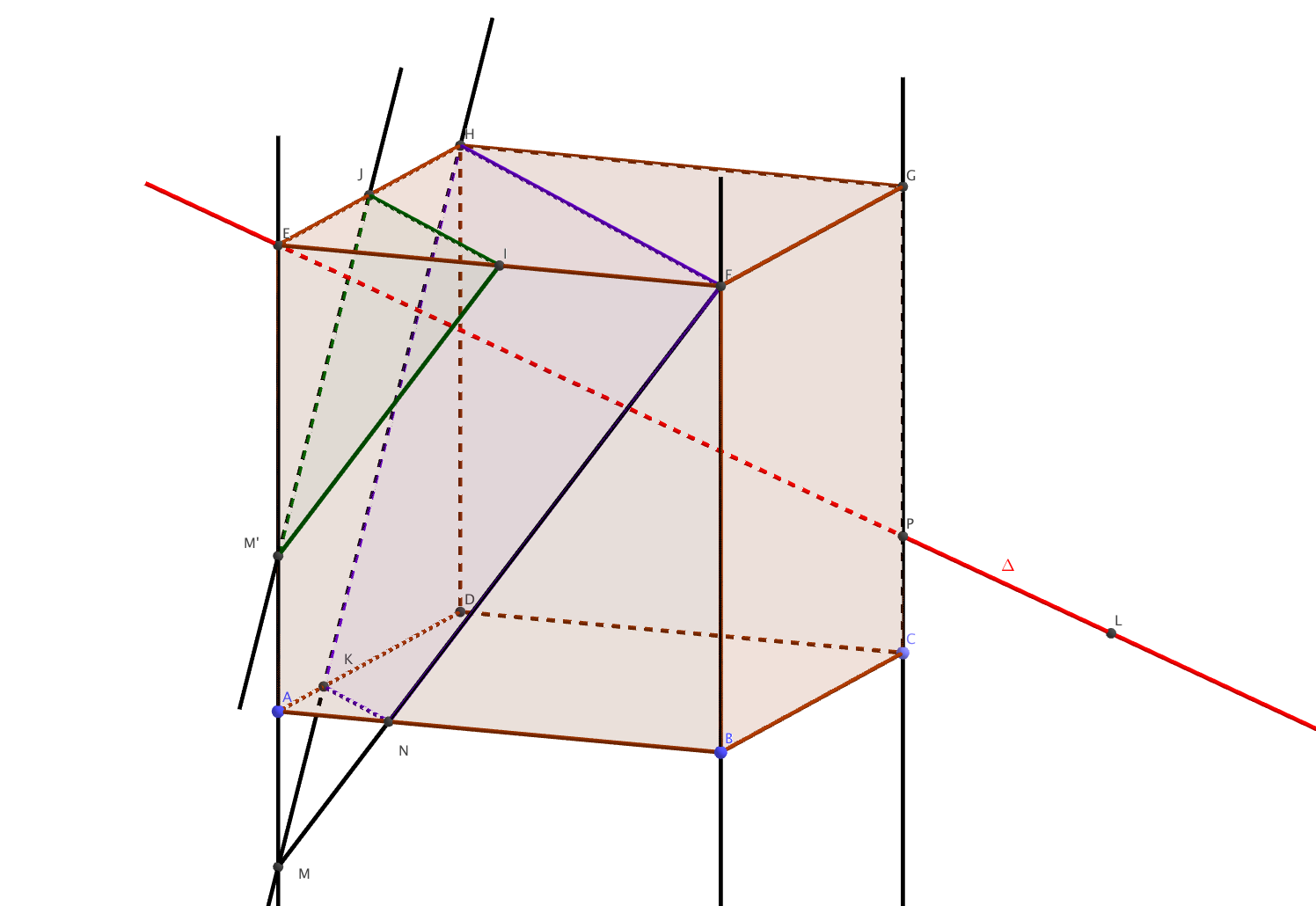
Figure :