Baccalauréat S Centres étrangers 10 juin 2015
Il est rappelé que la qualité de la rédaction, la clarté et la précision des raisonnements entreront pour une part importante dans l'appréciation des copies.
Exercice 1 5 points
Tous les résultats demandés dans cet exercice seront arrondis au millième.
Les parties A, B et C sont indépendantes.
Un fournisseur produit deux sortes de cadenas. Les uns sont premier prix, et les autres sont haut de gamme. Un magasin de bricolage dispose d'un stock de cadenas provenant de ce fournisseur; ce stock comprend un grand nombre de cadenas de chaque type.
Partie A
- Le fournisseur affirme que, parmi les cadenas haut de gamme, il n'y a pas plus de 3% de cadenas défectueux dans sa production. Le responsable du magasin de bricolage désire vérifier la validité de cette affirmation dans son stock ; à cet effet, il prélève un échantillon aléatoire de 500~cadenas haut de gamme, et en trouve 19 qui sont défectueux.
Ce contrôle remet-il en cause le fait que le stock ne comprenne pas plus de 3% de cadenas défectueux ? On pourra pour cela utiliser un intervalle de fluctuation asymptotique au seuil de 95%. - Le responsable du magasin souhaite estimer la proportion de cadenas défectueux dans son stock de cadenas premier prix. Pour cela il prélève un échantillon aléatoire de 500 cadenas premier prix , parmi lesquels 39 se révèlent défectueux.
Donner un intervalle de confiance de cette proportion au niveau de confiance 95%.
Partie B
D'après une étude statistique faite sur plusieurs mois, on admet que le nombre X de cadenas premier prix vendus par mois dans le magasin de bricolage peut être modélisé par une variable aléatoire qui suit la loi normale de moyenne $\mu = 750$ et d'écart-type $\sigma = 25$.
- Calculer $P(725 \leqslant X \leqslant 775)$.
- Le responsable du magasin veut connaître le nombre $n$ de cadenas premier prix qu'il doit avoir en stock en début de mois, pour que la probabilité d'être en rupture de stock en cours de mois soit inférieure à 0,05. On ne réalimente pas le stock en cours de mois .
Déterminer la plus petite valeur de l'entier $n$ remplissant cette condition.
Partie C
On admet maintenant que, dans le magasin :
- 80% des cadenas proposés à la vente sont premier prix, les autres haut de gamme ;
- 3% des cadenas haut de gamme sont défectueux ;
- 7% des cadenas sont défectueux.
On prélève au hasard un cadenas dans le magasin. On note :
- $p$ la probabilité qu'un cadenas premier prix soit défectueux ;
- $H$ l'évènement : « le cadenas prélevé est haut de gamme » ;
- $D$ l'évènement : « le cadenas prélevé est défectueux ».
- Représenter la situation à l'aide d'un arbre pondéré.
- Exprimer en fonction de $p$ la probabilité $P(D)$. En déduire la valeur du réel $p$. Le résultat obtenu est-il cohérent avec celui de la question A - 2. ?
- Le cadenas prélevé est en bon état. Déterminer la probabilité que ce soit un cadenas haut de gamme .
Correction de l'exercice 1 (5 points)
Tous les résultats demandés dans cet exercice seront arrondis au millième.
Les parties A, B et C sont indépendantes.
Un fournisseur produit deux sortes de cadenas. Les uns sont premier prix, et les autres sont haut de gamme. Un magasin de bricolage dispose d'un stock de cadenas provenant de ce fournisseur; ce stock comprend un grand nombre de cadenas de chaque type.
Partie A
- Le fournisseur affirme que, parmi les cadenas haut de gamme, il n'y a pas plus de 3% de cadenas défectueux dans sa production. Le responsable du magasin de bricolage désire vérifier la validité de cette affirmation dans son stock ; à cet effet, il prélève un échantillon aléatoire de 500 cadenas haut de gamme, et en trouve 19 qui sont défectueux.
Ce contrôle remet-il en cause le fait que le stock ne comprenne pas plus de 3% de cadenas défectueux ? On pourra pour cela utiliser un intervalle de fluctuation asymptotique au seuil de 95%. - Le responsable du magasin souhaite estimer la proportion de cadenas défectueux dans son stock de cadenas premier prix. Pour cela il prélève un échantillon aléatoire de 500 cadenas premier prix , parmi lesquels 39 se révèlent défectueux.
Donner un intervalle de confiance de cette proportion au niveau de confiance 95%. - On arrondit la borne inférieure par défaut à $10^{-\7}$ près : $\1 - \dfrac{1}{\sqrt{\2}}\approx \10$ soit $\5$.
- On arrondit la borne supérieure par excés à $10^{-\7}$ près : $\1 + \dfrac{1}{\sqrt{\2}}\approx \11$ soit $\6$.
La proportion $p$ est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times p $=\3 et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.
L'intervalle de fluctuation asymptotique au seuil de $95\% $ est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$
La fréquence observée est $f = \dfrac{19}{500} = 0,038 \in I_{500}$.
Ce contrôle ne remet donc pas en cause, au risque de $5\%$, l’affirmation du fournisseur.
$\quad$
La fréquence est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times \8 =\3$ et $n\times (1-\8)=\4,$ les conditions d'utilisation d'un intervalle de confiance sont réunies.
L' intervalle de confiance avec un niveau de confiance de 95% est : \[I = \left[f - \dfrac{1}{\sqrt{n}}~;~f +\dfrac{1}{\sqrt{n}} \right]\]
La fréquence est $\8=\1$.
L'intervalle de confiance au niveau de 95% est \[\9 = \left[\1 - \dfrac{1}{\sqrt{\2}}~;~\1 + \dfrac{1}{\sqrt{\2}} \right]\approx[\5~;~\6]\]
Partie B
D'après une étude statistique faite sur plusieurs mois, on admet que le nombre X de cadenas premier prix vendus par mois dans le magasin de bricolage peut être modélisé par une variable aléatoire qui suit la loi normale de moyenne $\mu = 750$ et d'écart-type $\sigma = 25$.
- Calculer $P(725 \leqslant X \leqslant 775)$.
- Le responsable du magasin veut connaître le nombre $n$ de cadenas premier prix qu'il doit avoir en stock en début de mois, pour que la probabilité d'être en rupture de stock en cours de mois soit inférieure à 0,05. On ne réalimente pas le stock en cours de mois .
Déterminer la plus petite valeur de l'entier $n$ remplissant cette condition. On cherche donc la valeur de $n$ telle que $P(X>n) = 0,05$
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
Remarque : Une propriété du cours nous la donne aussi :
Si $X$ suit $\mathcal{N}(\mu; \sigma)$, alors : $$P(\mu- \sigma \leqslant X \leqslant \mu+ \sigma)\approx 0,683$$
Ou encore $P(X \le n) = 0,95$.
A l’aide de la touche « invnorm » ou « normalFRép » de la calculatrice, on trouve $n= 792$ (on arrondit par excès).
2ND DISTR 2Fracnormale( \1 , \2, \3 )EXE
Avec une calculatrice de type TI $FracNormale(\1,\2,\3) \approx \4$
$\quad$
Une autre méthode consiste à se ramener à la loi normale centrée réduite:
En effet $Z=\dfrac{X-\mu}{\sigma}=\dfrac{X-750}{25} $ suit $\mathcal{N}(0;1)$ $$\begin{array}{rl} P(X \le n) = 0,95 & \iff P\left(\dfrac{X-750}{25} \le \dfrac{n-750}{25}\right) = 0,95 \\ &\iff P\left(Z \le \dfrac{n-750}{25}\right) = 0,95 \\ &\iff \pi\left(\dfrac{n-750}{25}\right)=0,95\\ &\iff \dfrac{n-750}{25} = \pi^{-1}(0,95) \\ &\iff n-750 = 25\pi^{-1}(0,95) \\ &\iff n = 750 + 25\pi^{-1}(0,95) \\ &\iff n = 750 + 25FracNormale(0,95) \\ &\iff n \approx 791,1 \\ \end{array}$$
Partie C
On admet maintenant que, dans le magasin :
- 80% des cadenas proposés à la vente sont premier prix, les autres haut de gamme ;
- 3% des cadenas haut de gamme sont défectueux ;
- 7% des cadenas sont défectueux.
On prélève au hasard un cadenas dans le magasin. On note :
- $p$ la probabilité qu'un cadenas premier prix soit défectueux ;
- $H$ l'évènement : « le cadenas prélevé est haut de gamme » ;
- $D$ l'évènement : « le cadenas prélevé est défectueux ».
- Représenter la situation à l'aide d'un arbre pondéré.
- Exprimer en fonction de $p$ la probabilité $P(D)$. En déduire la valeur du réel $p$. Le résultat obtenu est-il cohérent avec celui de la question A - 2. ? D’après la formule des probabilités totales on a :
- Le cadenas prélevé est en bon état. Déterminer la probabilité que ce soit un cadenas haut de gamme . On veut calculer :
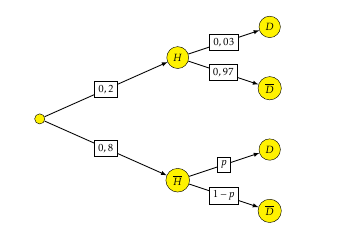
$$\begin{array}{rl} p(D) &= p(H \cap D) + p\left(\overline{H} \cap D\right) \\ 0,07&= 0,2 \times 0,03 + 0,8p \\ 0,07 & = 0,006 + 0,8p \\ 0,064 &= 0,8p \\ p&= \dfrac{0,064}{0,8}\\ p&= 0,08
\end{array}$$
$\quad$ $0,08 \in [0,033;0,123]$.
Ce résultat est donc cohérent avec celui de la question A-2.
$\quad$
$$\begin{array}{rl} P_{\overline{D}}(H) &= \dfrac{p\left(\overline{D}\cap H\right)}{p\left(\overline{D}\right)} \\ &=\dfrac{0,2 \times 0,97}{1 – 0,07} \\ & \approx 0,209
\end{array}$$
Exercice 2 4 points
Pour chacune des quatre affirmations suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.
Il est attribué un point par réponse exacte correctement justifiée.
Une réponse non justifiée n'est pas prise en compte. Une absence de réponse n'est pas pénalisée.
- Dans le plan muni d'un repère orthonormé, on note $S$ l'ensemble des points $M$ dont l'affixe $z$ vérifie les deux conditions : \[|z - 1| = |z - \text{i}|\quad \text{et} \quad |z - 3 - 2\text{i}| \leqslant 2.\]
Sur la figure ci-contre, on a représenté le cercle de centre le point de coordonnées (3 ; 2) et de rayon 2, et la droite d'équation $y = x$. Cette droite coupe le cercle en deux points A et B.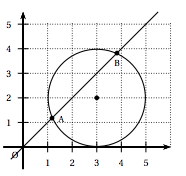
- Affirmation 1 : l'ensemble $S$ est le segment [AB].
- Affirmation 2 : le nombre complexe $\left(\sqrt{3} +\text{i}\right)^{ 1515 }$ est un réel.
Pour les questions 3 et 4, on considère les points E (2 ; 1 ; - 3), F (1 ; -1 ; 2) et G (-1 ; 3 ; 1) dont les coordonnées sont définies dans un repère orthonormé de l'espace. - Affirmation 3 : une représentation paramétrique de la droite (EF) est donnée par: \[\left\{\begin{array}{l c r} x&=&2t\\ y&=&-3 + 4t\\ z&=&7-10t \end{array}\right., t\: \in \mathbb R.\]
- Affirmation 4 : une mesure en degré de l'angle géométrique $\widehat{\text{FEG}}$, arrondie au degré, est 50°.
Correction de l'exercice 2 (4 points)
Pour chacune des quatre affirmations suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.
Il est attribué un point par réponse exacte correctement justifiée.
Une réponse non justifiée n'est pas prise en compte. Une absence de réponse n'est pas pénalisée.
- Dans le plan muni d'un repère orthonormé, on note $S$ l'ensemble des points $M$ dont l'affixe $z$ vérifie les deux conditions : \[|z - 1| = |z - \text{i}|\quad \text{et} \quad |z - 3 - 2\text{i}| \leqslant 2.\]
Sur la figure ci-contre, on a représenté le cercle de centre le point de coordonnées (3 ; 2) et de rayon 2, et la droite d'équation $y = x$. Cette droite coupe le cercle en deux points A et B.
- Affirmation 1 : l'ensemble $S$ est le segment [AB]. L’ensemble des points $M(z)$ vérifiant $|z-1| = |z-\text{i}|$ est la médiatrice du segment $[CD]$ avec $C(1)$ et $D(\text{i})$. Il s’agit donc de la droite d’équation $y=x$.
- Affirmation 2 : le nombre complexe $\left(\sqrt{3} +\text{i}\right)^{ 1515 }$ est un réel. $\left|\sqrt{3} + \text{i}\right| = \sqrt{3 + 1} = 2$.
En effet $$\begin{array}{rl} |z-1| = |z-\text{i}|&\iff |z_M-z_C| = |z_M-z_D|\\ &\iff CM = DM\\ &\iff M \text{ est équidistanrt de } C \text { et } D\\ \end{array}$$
L’ensemble des points vérifiant $|z – 3 – 2\text{i}| \le 2$ est le disque ce centre $E(3;2)$ et de rayon $2$ .
$$\begin{array}{rl} |z – 3 – 2\text{i}| \le 2&\iff |z_M-z_E| \le 2\\ &\iff EM \le 2\\ &\iff M \text{ est sur le disque ce centre } E(3;2) \text{et de rayon } 2 \\ \end{array}$$
L’ensemble $S$ est donc l’intersection de cette droite et de ce disque.
Il s’agit donc bien du segment $[AB]$.
Affirmation 1 : vraie
$\quad$
Ainsi
$$\begin{array}{rl} \sqrt{3} + \text{i} &= 2 \left(\dfrac{\sqrt{3}}{2} + \dfrac{\text{i}}{2}\right) \\ &= 2\text{e}^{\text{i}\frac{\pi}{6}}
\end{array}$$
Ainsi
$$\begin{array} {rl} \left(\sqrt{3}+\text{i}\right)^{1515} &= 2^{1515}\text{e}^{\text{i}\frac{1515pi}{6}} \\ &=2^{1515}\text{e}^{252,5\text{i}\pi} \end{array}$$
Or $252,5\pi$ n’est pas un multiple entier de $2\pi$. Par conséquent $ \text{e}^{252,5\text{i}\pi}$ n’est pas un nombre réel.
Affirmation 2 : fausse
$\quad$
Pour les questions 3 et 4, on considère les points E (2 ; 1 ; - 3), F (1 ; -1 ; 2) et G (-1 ; 3 ; 1) dont les coordonnées sont définies dans un repère orthonormé de l'espace. - Affirmation 3 : une représentation paramétrique de la droite (EF) est donnée par: \[\left\{\begin{array}{l c r} x&=&2t\\ y&=&-3 + 4t\\ z&=&7-10t \end{array}\right., t\: \in \mathbb R.\] Si on prend $t = 1$ alors le système nous donne :
- Affirmation 4 : une mesure en degré de l'angle géométrique $\widehat{\text{FEG}}$, arrondie au degré, est 50 °. $\vec{EF}(-1;-2;5)$ et $\vec{EG}(-3;2;4)$.
$\begin{cases} x=2 \times 1 = 2 \\\\y=-3 + 4\times 1 = 1 \\\\z= 7 – 10 \times 1 = -3\end{cases}$
On obtient les coordonnées de $E$.
$\quad$
Si on prend $t = 0,5$ alors le système nous donne :
$\begin{cases} x=2 \times 0,5 = 1 \\\\y=-3 + 4\times 0,5 = -1 \\\\z= 7 – 10 \times 0,5 = 2\end{cases}$
On obtient les coordonnées de $F$.
Il s’agit donc bien d’une représentation paramétrique de la droite $(EF)$.
Affirmation 3 : vraie
$\quad$
Ainsi $\vec{EF}.\vec{EG} = 3 – 4 + 20 = 19$.
$\quad$De plus $EF = \sqrt{1 + 4 + 25} = \sqrt{30}$ et $EG=\sqrt{9 + 4 + 16} = \sqrt{29}$.
Donc $\vec{EF}.\vec{EG} = \sqrt{30} \times \sqrt{29} \times \cos \left(\vec{EF},\vec{EG}\right) $
Par conséquent $\cos \left(\vec{EF},\vec{EG}\right) = \dfrac{19}{\sqrt{30} \times \sqrt{29}}$
D’où $\cos \widehat{EFG} \approx 49,90° \approx 50°$.
Affirmation 4 : vraie
$\quad$
Exercice 3 7 points
Soit $a$ un nombre réel fixé non nul. Le but de cet exercice est d'étudier la suite $\left(u_n\right)$ définie par: \[u_0 = a\quad \text{et, pour tout}\: n\: \text{de}\:\: \mathbb N,\quad u_{n+1} = \text{e}^{2u_n} - \text{e}^{u_n}.\] On remarquera que cette égalité peut aussi s'écrire : $u_{n+1} = \text{e}^{u_n}\left(\text{e}^{u_n} - 1\right)$.
- Soit $g$ la fonction définie pour tout réel $x$ par : \[g(x) = \text{e}^{2x} - \text{e}^{x} - x.\]
- Calculer $g '(x)$ et prouver que, pour tout réel $x $ : $g'(x) = \left(\text{e}^{x} - 1\right)\left(2\text{e}^{x} + 1\right)$.
- Déterminer les variations de la fonction $g$ et donner la valeur de son minimum.
- En remarquant que $u_{n+1} - u_n = g\left(u_n\right)$, étudier le sens de variation de la suite $\left(u_n\right)$.
- Dans cette question, on suppose que $a \leqslant 0$.
- Démontrer par récurrence que, pour tout entier naturel $n$, $u_n \leqslant 0$.
- Déduire des questions précédentes que la suite $\left(u_n\right)$ est convergente.
- Dans le cas où $a$ vaut $0$, donner la limite de la suite $\left(u_n\right)$.
- Dans cette question, on suppose que $a > 0$. La suite $\left(u_n\right)$ étant croissante, la question 1. permet d'affirmer que, pour tout entier naturel $n$, $u_n\geqslant a$.
- Démontrer que, pour tout entier naturel $n$, on a : $u_{n+1} - u_n \geqslant g(a)$.
- Démontrer par récurrence que, pour tout entier naturel $n$, on a : $u_n \geqslant a + n \times g(a)$.
- Déterminer la limite de la suite $\left(u_n\right)$.
- Dans cette question, on prend $a = 0,02$. L'algorithme suivant a pour but de déterminer le plus petit entier $n$ tel que $u_n > M$, où $M$ désigne un réel positif. Cet algorithme est incomplet. $$ \begin{array}{|r|l|} \hline \text{Variables}& n \text{ est un entier ,} u \text{ et } M \text{sont deux réels }\\ \hline & u \text{ prend la valeur } 0,02 \\ \text{Initialisation}& n \text{ prend la valeur } 0\\ &\text{ Saisir la valeur de } M \\ \hline \text{ Traitement}& \text{ Tant que } \ldots\\ &\ldots\\ &\ldots\\ &\text{ Fin tant que } \\ \hline \text{Sortie}& \text{ Afficher } n \\ \hline \end{array} $$
- Sur la copie, recopier la partie « Traitement » en la complétant.
- À l'aide de la calculatrice, déterminer la valeur que cet algorithme affichera si $M = 60$.
Correction de l'exercice 3 (5 points)
Soit $a$ un nombre réel fixé non nul. Le but de cet exercice est d'étudier la suite $\left(u_n\right)$ définie par: \[u_0 = a\quad \text{et, pour tout}\: n\: \text{de}\:\: \mathbb N,\quad u_{n+1} = \text{e}^{2u_n} - \text{e}^{u_n}.\] On remarquera que cette égalité peut aussi s'écrire : $u_{n+1} = \text{e}^{u_n}\left(\text{e}^{u_n} - 1\right)$.
- Soit $g$ la fonction définie pour tout réel $x$ par : \[g(x) = \text{e}^{2x} - \text{e}^{x} - x.\]
- Calculer $g '(x)$ et prouver que, pour tout réel $x $ : $g'(x) = \left(\text{e}^{x} - 1\right)\left(2\text{e}^{x} + 1\right)$. La fonction $g$ est dérivable sur $\mathbb R$ en tant que somme de fonctions dérivable sur $\mathbb R$.D’une part : $g'(x) = 2\text{e}^{2x} – \text{e}^x – 1$.
- Déterminer les variations de la fonction $g$ et donner la valeur de son minimum. La fonction exponentielle étant toujours positive, on en déduit que $2\text{e}^x + 1 > 0$. Le signe de $g'(x)$ ne dépend donc que de celui de $\text{e}^x – 1$.
- En remarquant que $u_{n+1} - u_n = g\left(u_n\right)$, étudier le sens de variation de la suite $\left(u_n\right)$. $$\begin{array}{rl} u_{n+1} – u_n &= e^{u_n}\left(\text{e}^{u_n} – 1\right) – u_n\\ &= e^{2u_n} – e^{u_n} – u_n \\ &= g\left(u_n\right) \end{array}$$D’après la question précédente, on peut donc dire que, pour tout réel $x$, on a $g(x) \ge 0$.Par conséquent $u_{n+1} – u_n \ge 0$.La suite $(u_n)$ est donc croissante.
- Dans cette question, on suppose que $a \leqslant 0$.
- Démontrer par récurrence que, pour tout entier naturel $n$, $u_n \leqslant 0$. Initialisation : $n=0$ alors $u_0 =a \le 0$
- Déduire des questions précédentes que la suite $\left(u_n\right)$ est convergente. La suite $(u_n)$ est croissante et majorée par $0$. Elle est donc convergente.
D’autre part : $$\begin{array}{rl} \left(\text{e}^x – 1\right)\left(2\text{e}^x + 1\right) &= 2\text{e}^{2x} + \text{e}^x – 2\text{e}^x – 1 \\ &= 2\text{e}^{2x} – \text{e}^x – 1\end{array}$$ Donc $g'(x) = \left(\text{e}^x – 1\right)\left(2\text{e}^x + 1\right)$
Or $\text{e}^x – 1 \ge 0 \iff \text{e}^x \ge 1 \iff x \ge 0$.La fonction $g$ est donc décroissante sur $]-\infty;0]$ et croissante sur $[0;+\infty[$. Elle admet un minimum pour $x=0$ et son minimum est $g(0) = 0$.
La propriété est vraie au rang $0$.
Hérédité : Supposons la propriété vraie au rang $n$ : $u_n \le 0$.
$u_{n+1} = \text{e}^{u_n}\left(\text{e}^{u_n} – 1\right)$.
La fonction exponentielle est toujours positive.
Puisque $u_n \le 0$ alors $e^{u_n} \le 0$. Donc $\text{e}^{u_n} – 1 \le 0$.
Par conséquent $u_{n+1} \le 0$.
La propriété est donc vraie au rang $n+1$.
Conclusion : La propriété est vraie au rang $0$ et elle est héréditaire.
Par conséquent, pour tout entier naturel $n$ on a : $u_n \le 0$.
- Dans le cas où $a$ vaut $0$, donner la limite de la suite $\left(u_n\right)$. Si $a=0$ alors $u_0 = 0$.
- La suite $(u_n)$ est croissante, majorée par $0$ et $u_0 = 0$. Par conséquent, pour tout entier naturel $n$, $u_n = 0$.
- La suite $(u_n)$ est donc constante et sa limite est $0$.
- $\quad$
- Dans cette question, on suppose que $a > 0$. La suite $\left(u_n\right)$ étant croissante, la question 1. permet d'affirmer que, pour tout entier naturel $n$, $u_n\geqslant a$.
- Démontrer que, pour tout entier naturel $n$, on a : $u_{n+1} - u_n \geqslant g(a)$. D’après la question
- on a $u_{n+1} – u_n = g\left(u_n\right)$.
- Pour tout entier naturel $n$, on a $u_n \ge a \ge 0$.
- La fonction $g$ est croissante sur $[0;+\infty[$, par conséquent $g(u_n) \ge g(a)$.
- Ainsi $u_{n+1} – u_n \ge g(a)$.
- $\quad$
- Démontrer par récurrence que, pour tout entier naturel $n$, on a : $u_n \geqslant a + n \times g(a)$.
- Si $n=0$ alors $u_0 = a$ et $a + 0\times g(a) = a$.
- La propriété est donc vraie au rang $0$.
- $\quad$
Hérédité :- Supposons la propriété vraie au rang $n$ : $u_n \ge a + n \times g(a)$.
- $$\begin{array}{rl} u_{n+1} – u_n \ge g(a) & \iff u_{n+1} \ge u_n + g(a) \\ & \iff u_{n+1} \ge a + n \times g(a) + g(a) \\ & \iff u_{n+1} \ge a + (n+1) \times g(a) \end{array}$$
- La propriété est donc vraie au rang $n+1$.
- $\quad$
Conclusion :- La propriété est vraie au rang $0$ et héréditaire.
- Par conséquent, pour tout entier naturel $n$, on a $u_{n} \ge a + n \times g(a)$.
- $\quad$
- Déterminer la limite de la suite $\left(u_n\right)$. Puisque $a >0$, on a $g(a) \ge 0$. Ainsi $\lim\limits_{n \to +\infty} n \times g(a) = +\infty$.
- Par conséquent $\lim\limits_{n \to +\infty} u_n = +\infty$.
- $\quad$
- Dans cette question, on prend $a = 0,02$. L'algorithme suivant a pour but de déterminer le plus petit entier $n$ tel que $u_n > M$, où $M$ désigne un réel positif. Cet algorithme est incomplet. $$ \begin{array}{|r|l|} \hline \text{Variables}& n \text{ est un entier ,} u \text{ et } M \text{sont deux réels }\\ \hline & u \text{ prend la valeur } 0,02 \\ \text{Initialisation}& n \text{ prend la valeur } 0\\ &\text{ Saisir la valeur de } M \\ \hline \text{ Traitement}& \text{ Tant que } \ldots\\ &\ldots\\ &\ldots\\ &\text{ Fin tant que } \\ \hline \text{Sortie}& \text{ Afficher } n \\ \hline \end{array} $$
- Sur la copie, recopier la partie « Traitement » en la complétant. Tant que $u \le M$
- $\quad$ $u$ prend la valeur $\text{e}^u\left(\text{e}^u – 1\right)$
- $\quad$ $n$ prend la valeur $n+1$
- Fin Tant que
- $\quad$
- À l'aide de la calculatrice, déterminer la valeur que cet algorithme affichera si $M = 60$. Si $M=60$ alors l’algorithme affiche $36$
- $\quad$
Une figure interactive :
Exercice 4 5 points
Les parties A et B sont indépendantes
Le fabricant de cadenas de la marque « K » désire imprimer un logo pour son entreprise.
Ce logo a la forme d'une lettre majuscule K stylisée, inscrite dans un carré ABCD, de côté une unité de longueur, et respectant les conditions C1 et C2 suivantes:
$\bullet~~$Condition C1 : la lettre K doit être constituée de trois lignes :
- une des lignes est le segment [AD] ;
- une deuxième ligne a pour extrémités le point A et un point E du segment [DC] ;
- la troisième ligne a pour extrémité le point B et un point G situé sur la deuxième ligne.
$\bullet~~$Condition C2 : l'aire de chacune des trois surfaces délimitées par les trois lignes dessinées dans h le carré doit être comprise entre $0,3$ et $0,4$, l'unité d'aire étant celle du carré. Ces aires sont notées $r$, $s$, $t$ sur les figures ci-après.
Un atelier de design propose deux dessins possibles, représentés ci-dessous: 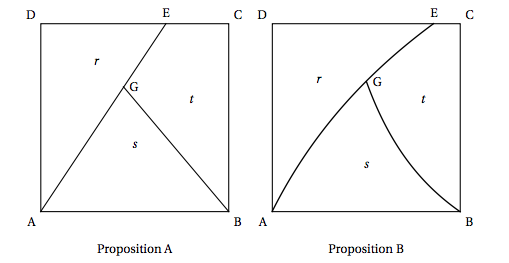
Pour mener les études qui suivent, on se place dans le repère orthonormé $\left(\text{A}~;~\vec{\text{AB}},~\vec{\text{AD}}\right)$.
Partie A : étude de la proposition A
Dans cette proposition les trois lignes sont des segments et les trois aires sont égales : $r = s = t = \dfrac{1}{3}$.
Déterminer les coordonnées des points E et G.
Partie B : étude de la proposition B
Cette proposition est caractérisée par les deux modalités suivantes:
$\bullet~~$la ligne d'extrémités A et E est une portion de la représentation graphique de la fonction $f$ définie pour tout réel $x \geqslant 0$ par : $f(x) = \ln (2x + 1)$ ;
$\bullet~~$la ligne d'extrémités B et G est une portion de la représentation graphique de la fonction $g$ définie pour tout réel $x > 0$ par : $g(x) = k\left(\dfrac{1 - x}{x}\right)$, où $k$ est un réel positif qui sera déterminé.
-
- Déterminer l'abscisse du point E.
- Déterminer la valeur du réel $k$, sachant que l'abscisse du point G est égale à $0,5$.
-
- Démontrer que la fonction $f$ admet pour primitive la fonction $F$ définie pour tout réel $x \geqslant 0$ par : \[F(x) = (x + 0,5) \times \ln (2x + 1) - x.\]
- Démontrer que $r = \dfrac{\text{e}}{2} - 1$.
- Déterminer une primitive $G$ de la fonction $g$ sur l'intervalle $]0~:~+ \infty[$.
- On admet que les résultats précédents permettent d'établir que $s = [\ln(2)]^2 + \dfrac{\ln (2) - 1}{2}$. La proposition B remplit-elle les conditions imposées par le fabricant?
Correction de l'exercice 4 5 points
Les parties A et B sont indépendantes
Le fabricant de cadenas de la marque « K » désire imprimer un logo pour son entreprise.
Ce logo a la forme d'une lettre majuscule K stylisée, inscrite dans un carré ABCD, de côté une unité de longueur, et respectant les conditions C1 et C2 suivantes:
$\bullet~~$Condition C1 : la lettre K doit être constituée de trois lignes :
- une des lignes est le segment [AD] ;
- une deuxième ligne a pour extrémités le point A et un point E du segment [DC] ;
- la troisième ligne a pour extrémité le point B et un point G situé sur la deuxième ligne.
$\bullet~~$Condition C2 : l'aire de chacune des trois surfaces délimitées par les trois lignes dessinées dans h le carré doit être comprise entre $0,3$ et $0,4$, l'unité d'aire étant celle du carré. Ces aires sont notées $r$, $s$, $t$ sur les figures ci-après.
Un atelier de design propose deux dessins possibles, représentés ci-dessous: 
Pour mener les études qui suivent, on se place dans le repère orthonormé $\left(\text{A}~;~\vec{\text{AB}},~\vec{\text{AD}}\right)$.
Partie A : étude de la proposition A
Déterminer les coordonnées des points E et G.
L’aire du triangle $ADE$ est donnée par $\dfrac{AD \times DE}{2}$. Or $AD = 1$
Par conséquent $\dfrac{DE}{2} = \dfrac{1}{3}$. D’où $DE = \dfrac{2}{3}$.
Ainsi le point $E$ a pour coordonnées $\left(\dfrac{2}{3};1\right)$
$\quad$
On appelle $G’$ le pied de la hauteur issue de $G$ dans le triangle $AGB$.
Son aire est $\dfrac{GG’ \times AB}{2}$. Avec $AB = 1$
Par conséquent $\dfrac{GG’}{2} = \dfrac{1}{3}$.
Donc $GG’ = \dfrac{2}{3}$
La droite $(AE)$ a pour équation $y=\dfrac{3}{2}x$.
L’abscisse $x$ du point $G$ vérifie donc l’équation $\dfrac{2}{3}=\dfrac{3}{2}x$.
Donc $x = \dfrac{4}{9}$.
Par conséquent le point $G$ a pour coordonnées $\left(\dfrac{4}{9};\dfrac{2}{3}\right)$
$\quad$
Partie B : étude de la proposition B
Cette proposition est caractérisée par les deux modalités suivantes:
$\bullet~~$la ligne d'extrémités A et E est une portion de la représentation graphique de la fonction $f$ définie pour tout réel $x \geqslant 0$ par : $f(x) = \ln (2x + 1)$ ;
$\bullet~~$la ligne d'extrémités B et G est une portion de la représentation graphique de la fonction $g$ définie pour tout réel $x > 0$ par : $g(x) = k\left(\dfrac{1 - x}{x}\right)$, où $k$ est un réel positif qui sera déterminé.
-
- Déterminer l'abscisse du point E. L’abscisse $x$ du point $E$ vérifie :
- Déterminer la valeur du réel $k$, sachant que l'abscisse du point G est égale à $0,5$. Le point $G$ appartient à la courbe représentative de la fonction $f$.
$$\begin{array}{rl} \ln(2x+1) = 1 &\iff 2x + 1 = \text{e} \\ &\iff 2x =\text{e} – 1 \\ &\iff x=\dfrac{\text{e} – 1}{2} \end{array}$$
$\quad$
Ainsi son ordonnée est :
$$ y=\ln (2 \times 0,5 + 1) = \ln 2$$.
Par conséquent
$$\begin{array}{rl} g(0,5) = \ln 2 & \iff k \left(\dfrac{1 – 0,5}{0,5}\right) = \ln 2 \\ & \iff k = \ln 2 \end{array}$$
$\quad$ -
- Démontrer que la fonction $f$ admet pour primitive la fonction $F$ définie pour tout réel $x \geqslant 0$ par : \[F(x) = (x + 0,5) \times \ln (2x + 1) - x.\] La fonction $F$ est dérivable sur $[0;+\infty[$ en tant que produit de fonctions dérivables sur cet intervalle.
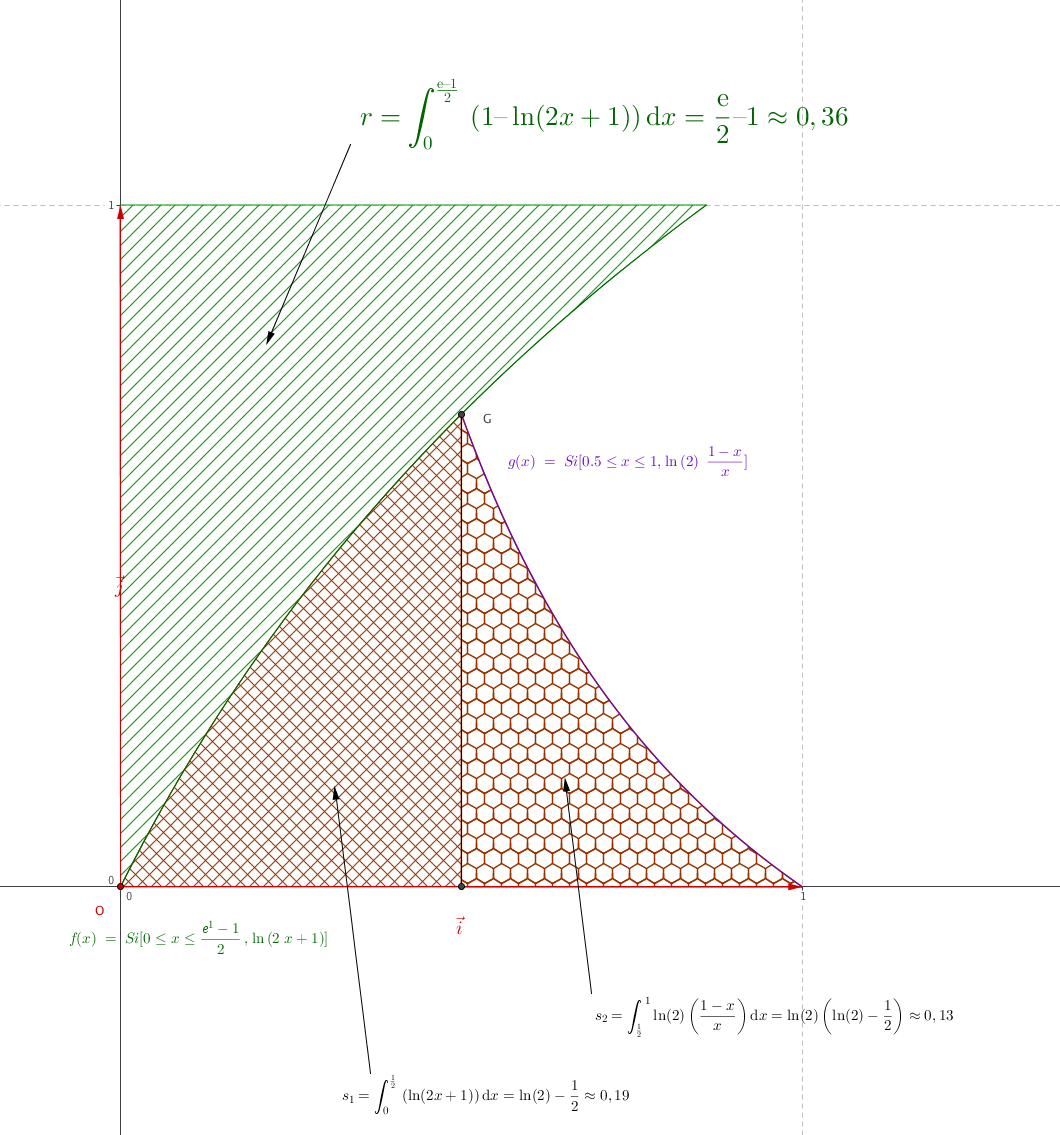
- Démontrer que $r = \dfrac{\text{e}}{2} - 1$. $r$ est du domaine délimité par les courbes des fonctions $f$ et $x \mapsto 1$ et les droites d’équation $x=0$ et $x= \dfrac{\text{e} – 1}{2}$ qui sont continues sur $\mathbb R^+$ donc sur $\left[ 0; \dfrac{\text{e} – 1}{2}\right]$; de plus sur cet intervalle la droite $D : y=1$ est située au dessus de $C_f$
$$\begin{array}{rl} F'(x) &= \ln(2x+1) + 2(x+0,5) \times \frac{1}{2x+1} – 1 \\ & = \ln(2x+1) + \dfrac{2x + 1}{2x+1} – 1 \\ & = \ln(2x+1) + 1 – 1 \\ & = f(x) \end{array}$$
la fonction $F$ est donc une primitive de la fonction $f$ sur $[0;+\infty[$.
Ainsi :
$$\begin{array}{rl} r &=\displaystyle \int_0^{\frac{\text{e} – 1}{2}} \left(1 – f(x)\right)\mathrm{d}x \\ &=\displaystyle \int_0^{\frac{\text{e} – 1}{2}} \left(1 – \ln(2x+1)\right)\mathrm{d}x \\ & = \left[x – F(x)\right]_0^{\frac{\text{e} – 1}{2}} \\ &= \dfrac{\text{e} – 1}{2} – \left[\left(\dfrac{\text{e} – 1}{2}+0,5\right)\ln \left(2\dfrac{\text{e} – 1}{2}+1\right) – \dfrac{\text{e} – 1}{2}\right] \\ &= \dfrac{\text{e} – 1}{2} – \dfrac{\text{e} }{2} + \dfrac{\text{e} – 1}{2} \\ & = \dfrac{\text{e} }{2} – 1 \end{array}$$ - Déterminer une primitive $G$ de la fonction $g$ sur l'intervalle $]0~:~+ \infty[$. On a $g(x) = \ln(2) \left(\dfrac{1}{x} – 1\right)$.
- On admet que les résultats précédents permettent d'établir que $s = [\ln(2)]^2 + \dfrac{\ln (2) - 1}{2}$. La proposition B remplit-elle les conditions imposées par le fabricant? On a $r \approx 0,359$ et $s \approx 0,327$. Ainsi $t = 1 -r -s \approx 0,314$.
La fonction $g$ est continue sur $]0;+\infty[$.
Une primitive $G$ est définie sur cet intervalle par :
$$G(x) = \ln(2) \left(\ln(x) – x\right)$$
La proposition B vérifie donc les conditions imposées par le fabriquant.
Spécialité 5 points
Dans cet exercice, on s'intéresse aux triplets d'entiers naturels non nuls $(x,~y,~z)$ tels que \[x ^2 + y^2 = z^2.\] Ces triplets seront nommés « triplets pythagoriciens » en référence aux triangles rectangles dont ils mesurent les côtés, et notés en abrégé « TP ». Ainsi (3, 4, 5) est un TP car $3^2 +4^2 = 9 + 16 = 25 = 5^2$.
Partie A : généralités
- Démontrer que, si $(x,~y,~z)$ est un TP, et $p$ un entier naturel non nul, alors le triplet $(px,~py,~pz)$ est lui aussi un TP.
- Démontrer que, si $(x,~y,~z)$ est un TP, alors les entiers naturels $x$, $y$ et $z$ ne peuvent pas être tous les trois impairs.
- Pour cette question, on admet que tout entier naturel non nul $n$ peut s'écrire d'une façon unique sous la forme du produit d'une puissance de 2 par un entier impair : $n = 2^{\alpha} \times k$ où $\alpha$ est un entier naturel (éventuellement nul) et $k$ un entier naturel impair. L'écriture $n = 2^{\alpha} \times k$ est nommée décomposition de $n$. Voici par exemple les décompositions des entiers 9 et 120 : $9 = 2^{0} \times 9,\quad 120 = 2^3 \times 15$.
- Donner la décomposition de l'entier $192$.
- Soient $x$ et $z$ deux entiers naturels non nuls, dont les décompositions sont $x = 2^{\alpha} \times k$ et $z=2^{\beta} \times m$. Écrire la décomposition des entiers naturels $2 x^2$ et $z^2 $.
- En examinant l'exposant de 2 dans la décomposition de $2x^2$ et dans celle de $z^2$ , montrer qu'il n'existe pas de couple d'entiers naturels non nuls $(x,~z)$ tels que $2x^2 = z^2$.
Partie B : recherche de triplets pythagoriciens contenant l'entier 2015
- Décomposer en produit de facteurs premiers l'entier 2015 puis, en utilisant le TP donné dans le préambule, déterminer un TP de la forme $(x,~y,~2015)$.
- On admet que, pour tout entier naturel $n$ , $(2n + 1)^2 + \left(2n^2 + 2n\right)^2 = \left(2n^2 + 2n + 1\right)^2$. Déterminer un TP de la forme $(2015,~ y,~ z )$.
-
- En remarquant que $403^2 =169 \times 961$, déterminer un couple d'entiers naturels non nuls $(x,~z)$ tels que : $z^2 - x^2 = 403^2$, avec $x < 403$.
- En déduire un TP de la forme $(x,~ 2015,~z)$.
Correction de l'exercice de Spécialité 5 points
Dans cet exercice, on s'intéresse aux triplets d'entiers naturels non nuls $(x,~y,~z)$ tels que \[x ^2 + y^2 = z^2.\] Ces triplets seront nommés « triplets pythagoriciens » en référence aux triangles rectangles dont ils mesurent les côtés, et notés en abrégé « TP ». Ainsi (3, 4, 5) est un TP car $3^2 +4^2 = 9 + 16 = 25 = 5^2$.
Partie A : généralités
- Démontrer que, si $(x,~y,~z)$ est un TP, et $p$ un entier naturel non nul, alors le triplet $(px,~py,~pz)$ est lui aussi un TP. Soient $(x,y,z)$ est un TP et $p$ est un entier naturel non nul.
- Démontrer que, si $(x,~y,~z)$ est un TP, alors les entiers naturels $x$, $y$ et $z$ ne peuvent pas être tous les trois impairs. Supposons que les trois entiers naturels $x$, $y$ et $z$ soient impairs .
- Pour cette question, on admet que tout entier naturel non nul $n$ peut s'écrire d'une façon unique sous la forme du produit d'une puissance de 2 par un entier impair : $n = 2^{\alpha} \times k$ où $\alpha$ est un entier naturel (éventuellement nul) et $k$ un entier naturel impair. L'écriture $n = 2^{\alpha} \times k$ est nommée décomposition de $n$. Voici par exemple les décompositions des entiers 9 et 120 : $9 = 2^{0} \times 9,\quad 120 = 2^3 \times 15$.
- Donner la décomposition de l'entier $192$. $192 = 2^6 \times 3$.
- Soient $x$ et $z$ deux entiers naturels non nuls, dont les décompositions sont $x = 2^{\alpha} \times k$ et $z=2^{\beta} \times m$. Écrire la décomposition des entiers naturels $2 x^2$ et $z^2 $. D’après la question précédente, on a vu que le carré d’un nombre impair est impair également.
- En examinant l'exposant de 2 dans la décomposition de $2x^2$ et dans celle de $z^2$ , montrer qu'il n'existe pas de couple d'entiers naturels non nuls $(x,~z)$ tels que $2x^2 = z^2$. Si $2x^2 = z^2$ alors $2^{2\alpha + 1} \times k^2 = 2^{2\beta} \times m^2$.
$x^2 = 2^{2\alpha}\times k^2 $ donc $2x^2 = 2^{2\alpha + 1} \times k^2$
$z^2 = 2^{2\beta} \times m^2$
Par conséquent $2\alpha + 1 = 2\beta$ soit $2(\beta – \alpha) = 1$. Ce qui impossible car $2(\beta – \alpha)$ est pair et $1$ impair.
Il n’existe donc pas d’entiers naturels non nuls $(x,y)$ tels que $2x^2=z^2$.
Alors
$\begin{array}{rl} (px)^2 + (py)^2 &= p^2(x^2+y^2) \\ &= p^2z^2 \\ &= (pz)^2
\end{array}$
Donc $(px,py,pz)$ est également un TP.
Soit $n$ un entier naturel, alors $(2n+1)^2 = 4n+ 4n + 1 \equiv 1~[2]$.
Ainsi $x^2 \equiv 1 ~[2]$ et $y^2 \equiv 1 ~[2]$ donc $x^2 + y^2 \equiv 0 ~[2]$.
Or $z^2 \equiv 1 ~[2]$.
On ne peut donc pas avoir $x^2+y^2 = z^2$.
$x$, $y$ et $z$ ne peuvent donc pas être tous les trois impairs.
Partie B : recherche de triplets pythagoriciens contenant l'entier 2015
- Décomposer en produit de facteurs premiers l'entier 2015 puis, en utilisant le TP donné dans le préambule, déterminer un TP de la forme $(x,~y,~2015)$. $2015 = 5 \times 13 \times 31$. Et $13 \times 31 = 403$
- On admet que, pour tout entier naturel $n$ , $(2n + 1)^2 + \left(2n^2 + 2n\right)^2 = \left(2n^2 + 2n + 1\right)^2$. Déterminer un TP de la forme $(2015,~ y,~ z )$.
- $2015 = 2 \times 1007 + 1$.
Ainsi le triplet $(2015,2\times 1007^2 + 2\times 1007, 2\times 1007 + 2\times 1007 + 1)$ est un TP soit $(2015,2~030~112,2~030~113)$ .
- En remarquant que $403^2 =169 \times 961$, déterminer un couple d'entiers naturels non nuls $(x,~z)$ tels que : $z^2 - x^2 = 403^2$, avec $x < 403$. On a $z^2-x^2 = (z-x)(z+x)$.
- En déduire un TP de la forme $(x,~ 2015,~z)$. Le triplet $(396,403,565)$ est un TP.
Par conséquent, on cherche les valeurs de $x$ et $z$ telles que :
$(z-x)(z+x) = 169 \times 961$.
Regardons s’il est possible de résoudre le système :
$$\begin{array}{rl} \begin{cases} z-x = 169 \\\\z+x = 961 \end{cases} &\iff \begin{cases} z=169+x \\\\169+2x=961 \end{cases} \\ & \iff \begin{cases} x= 396 \\\\z=565 \end{cases} \end{array}$$
Ainsi le couple $(396,565)$ convient.
Donc $(5 \times 396,5 \times 403, 5 \times 565)$ est également un TP.
Soit $(1980,2015,2825)$ est un TP.
Le triplet $(3,4,5)$ est un TP. Par conséquent le triplet $(3 \times 403,4 \times 403, 5 \times 403)$ est également un TP.
Ainsi le triplet $(1209,1612,2015)$ est un TP.
- Vues: 33036
