Baccalauréat S Asie 17 juin 2015
Page 1 sur 10
Exercice 1 5 points
- Les trois parties de cet exercice sont indépendantes. Les probabilités seront arrondies au millième.
- Le concurrent tire quatre flèches. On considère que les tirs sont indépendants. Déterminer la probabilité qu'il atteigne au moins trois fois la cible.
- Combien de flèches le concurrent doit-il prévoir pour atteindre en moyenne la cible douze fois ?
- si la flèche atteint le point A, le tireur a raté la bande, et $X$ prend la valeur $15$ ;
- si elle atteint le point B, l'impact est à la limite de la bande, et $X$ prend la valeur $10$ ;
- si elle atteint le point C, l'impact est dans la bande et $X$ prend la valeur $- 5$.
- Lorsque la flèche atteint le plan, déterminer la probabilité que son point d'impact soit situé hors de la bande grisée.
- Comment modifier les bords de la bande grisée pour faire en sorte que, lorsque la flèche atteint le plan, son point d'impact soit situé à l'intérieur de la bande avec une probabilité égale à $0,6$ ?
- Quelle est la probabilité que le panneau fonctionne au moins pendant 2000 heures ?
- Restitution organisée des connaissances
Dans cette question, $\lambda$ désigne un réel strictement positif. On rappelle que l'espérance mathématique de la variable aléatoire $T$ suivant une loi exponentielle de paramètre $\lambda$, est définie par : E$(T) = \displaystyle\lim_{x \to + \infty} \int_0^x\lambda t \text{e}^{- \lambda t}\text{d}t$.- On considère la fonction $F$, définie pour tout réel $t$ par : $F(t) = \left(- t - \dfrac{1}{\lambda}\right)\text{e}^{- \lambda t}$. Démontrer que la fonction $F$ est une primitive sur $\mathbb R$ de la fonction 1 définie pour tout réel $t$ par : $f(t) = \lambda t\text{e}^{- \lambda t}$.
- En déduire que l'espérance mathématique de la variable aléatoire $T$ est égale à $\dfrac{1}{\lambda}$. Quelle est l'espérance de durée de vie du panneau électrique affichant le score des concurrents ?
Partie A
Un concurrent participe à un concours de tir à l'arc, sur une cible circulaire. À chaque tir, la probabilité qu'il atteigne la cible est égale à $0$,8.
Partie B
Entre deux phases du concours, pour se perfectionner, le concurrent travaille sa précision latérale sur une autre cible d'entraînement, représentée ci-contre. Pour cela, il tire des flèches pour essayer d'atteindre une bande verticale, de largeur $20$ cm (en grisé sur la figure), le plus près possible de la ligne verticale centrale. On munit le plan contenant la bande verticale d'un repère : la ligne centrale visée est l'axe des ordonnées. On note $X$ la variable aléatoire qui, à toute flèche tirée atteignant ce plan, associe l'abscisse de son point d'impact.
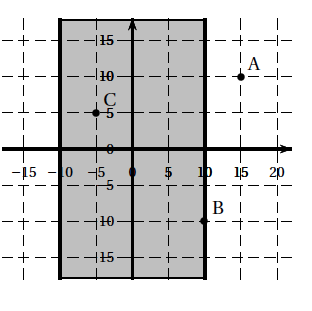
Ainsi, par exemple :
On suppose que la variable aléatoire $X$ suit une loi normale d'espérance $0$ et d'écart-type $10$.
Partie C
La durée de vie (exprimée en heures) du panneau électrique affichant le score des concurrents est une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $\lambda = 10^{-4}$ (exprimé en h$^{-1}$).
- Vues: 35605
