Baccalauréat S Asie 17 juin 2015 - Correction Exercice 3

Page 6 sur 10: Correction Exercice 3

Correction de l'exercice 3 (5 points)

Commun à tous les candidats

Fonctions

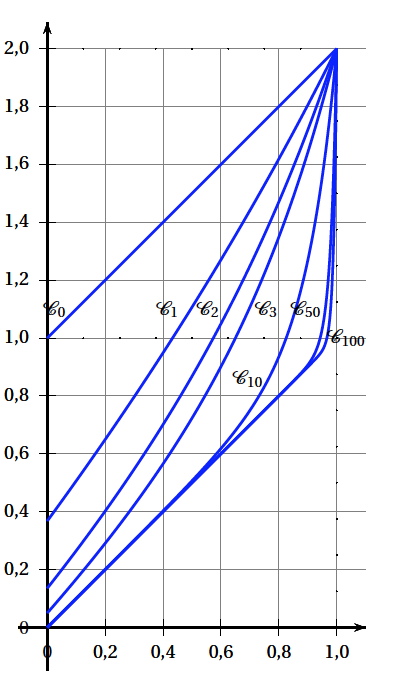
Pour tout entier naturel $n$, on définit la fonction $f_n$ pour tout réel $x$ de l'intervalle [0 ; 1] par : \[f_n(x) = x + \text{e}^{n (x - 1)}.\] On note $\mathcal{C}_n$ la représentation graphique de la fonction $f_n$ dans un repère orthogonal. Quelques-unes des courbes $\mathcal{C}_n$ sont représentées ci-dessous.

Partie A : généralités sur les fonctions $f_n$

1. Démontrer que, pour tout entier naturel $n$, la fonction $f_n$ est croissante et positive sur l'intervalle [0 ; 1].
Pour tout entier naturel $n$, la fonction $f_n$ est croissante sur $[0;1]$ en tant que somme de fonctions croissantes sur cet intervalle.
On peut aussi remarquer que la fonction $f_n$ estdérivables sur $[0;1]$ en tant que somme de fonctions dérivables sur cet intervalle.
$f_n'(x)=1+n\text{e}^{n (x - 1)}$

• Premier cas $n=0$
  $f_0(x)=x+ \text{e}^{0 (x - 1)}=x$
  $f_0'(x)=1> 0 $; ainsi $f_0$ est croissante et positive sur l'intervalle [0 ; 1].
• Deuxième cas : $n\geq 1$
  $f_n(x)=x+ \text{e}^{ n(x - 1)}=x$
  $f_n'(x)=1+ n\text{e}^{ (x - 1)}> 0 $; ainsi $f_n$ est croissante sur l'intervalle [0 ; 1].
$\quad$
De plus, sur $[0;1]$, $x \ge 0$ et la fonction exponentielle étant strictement positive sur $\mathbb R$, on a $\text{e}^{n(x-1)} > 0$.
Par conséquent, pour tout $x \in [0;1]$, $f_n(x) \ge 0$.

2. Montrer que les courbes $\mathcal{C}_n$ ont toutes un point commun A, et préciser ses coordonnées.
Montrons que le point $A(1;2)$ appartient à toutes les courbes $C_n$.
Pour tout entier naturel $n$, on a $f_n(1) = 1 + \text{e}^0 = 2$.
Le point $A(1;2)$ appartient bien à toutes les courbes $C_n$.

3. À l'aide des représentations graphiques, peut-on conjecturer le comportement des coefficients directeurs des tangentes en A aux courbes $\mathcal{C}_n$ pour les grandes valeurs de $n$ ? Démontrer cette conjecture.
Il semblerait que les coefficients directeurs des tangentes en A aux courbes $C_n$ soient les termes d’une suite croissante de limite $+\infty$.
$\quad$.
Pour tout entier naturel $n$, la fonction $f_n$ est dérivable sur $[0;1]$ en tant que somme de fonctions dérivables sur cet intervalle.
$ f_n'(x) = 1 +n\text{e}^{n(x-1)}$.
Or le coefficient directeur de la tangente en A à la courbe $C_n$ est donné par $f_n'(1) = 1 + n$.
La suite $(1+n)_{n\in \mathbb N}$ est clairement croissante et de limite $+\infty$.

Partie B : évolution de $f_n(x)$ lorsque $x$ est fixé

Soit $x$ un réel fixé de l'intervalle [0 ; 1] . Pour tout entier naturel $n$, on pose $u_n = f_n (x)$.

1. Dans cette question, on suppose que $x = 1$. Étudier la limite éventuelle de la suite $\left(u_n\right)$.
Si $x=1$, on a alors $u_n = 1 + 1 = 2$.
La suite $(u_n)$ est donc constante et a pour limite $2$.

2. Dans cette question, on suppose que $0 \leqslant x < 1$. Étudier la limite éventuelle de la suite $\left(u_n\right)$.
Si $0 \le x <1$ on a alors $u_n = x + \left(e^{x-1}\right)^n$.
Or $x-1 < 0 $ donc $0 < \text{e}^{x-1} < 1$ et $\lim\limits_{n \to +\infty} \left(e^{x-1}\right)^n = 0$.
Par conséquent $\lim\limits_{n \to +\infty} u_n = x$.

Partie C : aire sous les courbes $\mathcal{C}_n$

Le domaine délimité par la courbe $f_n$, l’axe des abscisses et les droites d’équation $x=0$ et $x=1$ semble se rapprocher de plus en plus d’un triangle rectangle isocèle de côté $1$. Par conséquent la limite de $A_n$ semble être $\dfrac{1}{2}$.

On a pour $n\geq 1$:

$$\begin{array}{rl} A_n & = \displaystyle \int_0^1 f_n(x) \mathrm{d}x\\ & = \left[\dfrac{x^2}{2} + \dfrac{1}{n}\text{e}^{n(x-1)}\right]_0^1\\ & = \dfrac{1}{2} + \dfrac{1}{n}\left(1 – \text{e}^{-n}\right) \end{array}$$
Or $\lim\limits_{n \to +\infty} e^{-n} = 0$ et $\lim\limits_{n \to +\infty} \dfrac{1}{n} = 0$.
Par conséquent, par somme et produit des limites $\lim\limits_{n \to +\infty} A_n = \dfrac{1}{2}$.

Une animation sous Geogebra