Baccalauréat S Polynésie 12 juin 2015
Page 1 sur 12
Exercice 1 3 points
On considère le pavé droit ABCDEFGH ci-dessous, pour lequel AB = 6, AD = 4 et AE = 2. I, J et K sont les points tels que $\vec{\text{AI}} = \dfrac{1}{6} \vec{\text{AB}},\:\: \vec{\text{AJ}} = \dfrac{1}{4} \vec{\text{AD}},\:\: \vec{\text{AK}} = \dfrac{1}{2} \vec{\text{AE}}$. 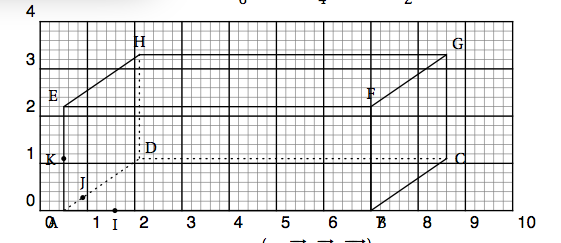
On se place dans le repère orthonormé $\left(\text{A}~;~ \vec{\text{AI}},~ \vec{\text{AJ}},~\vec{\text{AK}}\right)$.
- Vérifier que le vecteur $\vec{n}$ de coordonnées $\begin{pmatrix}2\\2\\- 9\end{pmatrix}$ est normal au plan (IJG).
- Déterminer une équation du plan (IJG).
- Déterminer les coordonnées du point d'intersection L du plan (IJG) et de la droite (BF).
- Tracer la section du pavé ABCDEFGH par le plan (IJG). Ce tracé sera réalisé sur la figure (donnée en annexe à rendre avec la copie) . On ne demande pas de justification.
Annexe 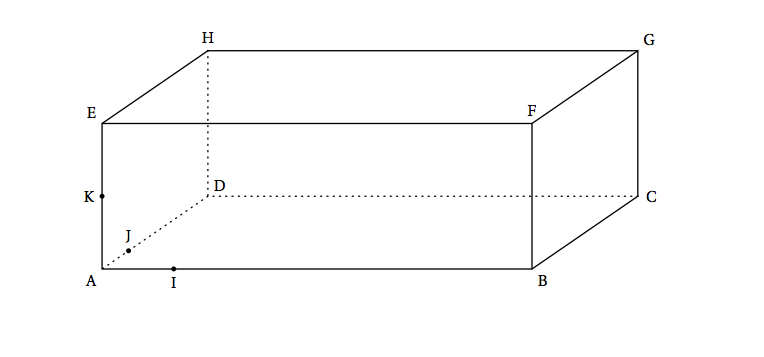
- Vues: 50445
