Baccalauréat S Antilles Guyane 22 juin 2015 - Correction Exercice 3
Page 6 sur 10
Correction de l'exercice 3 (5 points)
Partie A
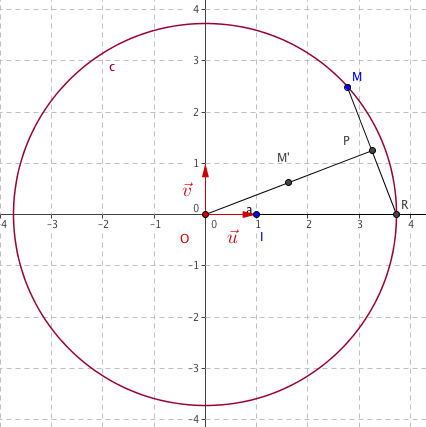
On appelle $\mathbb C$ l'ensemble des nombres complexes. Dans le plan complexe muni d'un repère orthonormé $\left(\text{O},~\vec{u},~\vec{v}\right)$ on a placé un point $M$ d'affixe $z$ appartenant à $\mathbb C$, puis le point $R$ intersection du cercle de centre O passant par $M$ et du demi-axe $\left[\text{O}~;~ \vec{u}\right)$.
- Exprimer l'affixe du point $R$ en fonction de $z$. L’affixe du point $R$ est donc $|z|$.
- Soit le point $M'$ d'affixe $z'$ définie par \[z' = \dfrac{1}{2}\left(\dfrac{z + |z|}{2}\right) .\] Reproduire la figure sur la copie et construire le point $M'$. Comme $M$ a pour affixe $z$ et $R$ a pour affixe $|z|$, $\dfrac{z + |z|}{2} $ est l'affixe du point $P$ mileu de $[MR]$.
Pour finir $O$ a pour affixe $0$ et $P$ a pour affixe $\dfrac{z + |z|}{2} $, donc $M'$ d'affixe $\dfrac{1}{2}\left(\dfrac{z + |z|}{2}\right)$ est le milieu du segment $[OP]$.
Partie B
On définit la suite de nombres complexes $\left(z_n\right)$ par un premier terme $z_0$ appartenant à $\mathbb C$ et, pour tout entier naturel $n$, par la relation de récurrence : \[z_{n + 1} = \dfrac{z_n + \left|z_n \right|}{4}.\] Le but de cette partie est d'étudier si le comportement à l'infini de la suite $\left(\left|z_n\right|\right)$ dépend du choix de $z_0$.
- Que peut-on dire du comportement à l'infini de la suite $\left(\left|z_n\right|\right)$ quand $z_0$ est un nombre réel négatif ? Si $z_0$ est un nombre réel négatif alors $z_0 + |z_0| = z_0 -z_0 =0$
- Que peut-on dire du comportement à l'infini de la suite $\left(\left|z_n\right|\right)$ quand $z_0$ est un nombre réel positif ? Si $z_0$ est un nombre réel positif, alors $z_0 + |z_0| = 2z_0$.
- On suppose désormais que $z_0 $n'est pas un nombre réel.
- Quelle conjecture peut-on faire sur le comportement à l'infini de la suite $\left(\left|z_n\right|\right)$ ? On peut émettre la conjecture que la suite $\left(\left|z_n\right|\right)$ converge vers $0$.
- Démontrer cette conjecture, puis conclure. On a $\left|z_{n+1}\right| = \left|\dfrac{z_n + \left|z_n\right|}{4}\right| \le \dfrac{2\left|z_n\right|}{4}$
$\quad$
On utilise ici la propriété valable pour tous nombres complexes $z$ et $z'$ : $$ \left| z + z'\right| \le \left| z \right| + \left| z'\right|$$ Donc $0 \le \left|z_{n+1}\right| \le \dfrac{\left|z_n\right|}{2}$
Or la suite $\left(\dfrac{\left|z_n\right|}{2}\right)$ est une suite géométrique de raison $\dfrac{1}{2}$ qui converge donc vers $0$.
$\quad$
D’après le théorème des gendarmes, la suite $\left(\left|z_n\right|\right)$ converge donc vers $0$.
$\quad$
Ainsi, pour tout nombre complexe $z_0$, la suite $\left(\left|z_n\right|\right)$ converge vers $0$.
Ainsi $z_1 = 0$ et $z_n = 0$ pour tout entier naturel non nul $n$.
La suite $\left(\left|z_n\right|\right)$ est donc constante à partir du rang $1$.
Par conséquent $z_1 = \dfrac{z_0}{2}$
Ainsi $z_{n+1} = \dfrac{z_n}{2}$. Donc $\left(\left|z_n\right|\right)$ est géométrique de raison $\dfrac{1}{2}$.
$\quad$
La suite $\left(\left|z_n\right|\right)$ est donc décroissante et converge vers $0$.
- Vues: 41402
