Baccalauréat S Nouvelle-Calédonie Mars 2017 - Correction Exercice 1

Page 2 sur 10: Correction Exercice 1

Correction de l'exercice 1 (5 points)

Commun à tous les candidats

On considère la fonction $f$ définie et dérivable sur $[0~;~ +\infty[$ par \[f(x) = x\text{e}^{- x}\] et on note $\mathcal{C}_f$ sa courbe représentative dans un repère orthogonal.

Partie A

 

1. Justifier toutes les informations du tableau de variations de $f$ donné ci-dessous.
   
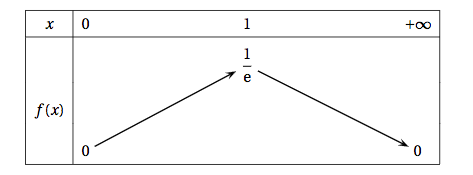$f(0)=0\times \text{e}^{-0}=0\times 1 = 0$
$f(x)=-(-x)\text{e}^{-x}$
$\left.\begin{array}{l}\lim\limits_{x\to+\infty} -x=-\infty \\
\lim\limits_{X \to -\infty}X\text{e}^X=0\end{array}\right\}$ donc $\lim\limits_{x \to +\infty} f(x)=0$
La fonction $f$ est dérivable sur $[0;+\infty[$ en tant que produit de fonctions dérivables sur cet intervalle.
$f'(x)=\text{e}^{-x}-x\text{e}^{-x}=(1-x)\text{e}^{-x}$
La fonction exponentielle est strictement positive.
Par conséquent le signe de $f'(x)$ ne dépend que de celui de $1-x$.
Or $1-x>0 \iff x<1$ et $1-x=0\iff x=1$
On en déduit donc que la fonction $f$ est croissante sur l’intervalle $[0;1]$ et décroissante sur l’intervalle $[1;+\infty[$.
De plus $f(1)=1\times \text{e}^{-1}=\dfrac{1}{\text{e}}$.

2. Soit $F$ la fonction définie et dérivable sur $[0~;~ +\infty[$ par \[F(x) = (- x - 1)\text{e}^{- x}.\] Démontrer que la fonction $F$ est une primitive de $f$ sur $[0~;~+\infty[$.
$F$ est dérivable sur $[0;+\infty[$ d’après l’énoncé.
$F'(x)=-1\times \text{e}^{-x}-(-x-1)\text{e}^{-x}=(-1+x+1)\text{e}^{-x}=x\text{e}^{-x}=f(x)$.
La fonction $F$ est donc une primitive de la fonction $f$ sur l’intervalle $[0;+\infty[$.

 

Partie B

Soit $a$ un nombre réel tel que $0 < a < 1$. On considère la droite $D_a$ d'équation $y = ax$ et $M$ le point d'intersection de la droite $D_a$ avec la courbe $\mathcal{C}_f$. On note $x_M$ l'abscisse du point $M$. On note $\mathcal{H}(a)$ l'aire, exprimée en unités d'aire, du domaine hachuré sur le graphique ci-dessous, c'est-à-dire du domaine situé sous la courbe $\mathcal{C}_f$ au-dessus de la droite $D_a$ et entre les droites d’équation $x = 0$ et $x = x_M$. Le but de cette partie est d'établir l'existence et l'unicité de la valeur de $a$ telle que $\mathcal{H}(a) = 0,5$ puis d'étudier un algorithme.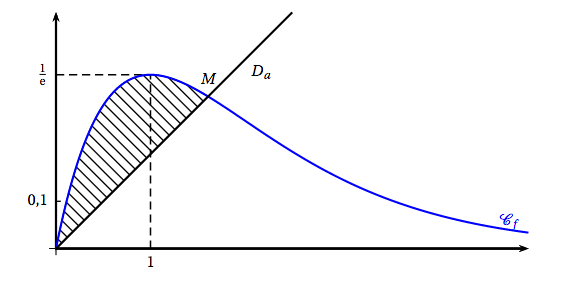

1. Prouver que la droite $D_a$ et la courbe $\mathcal{C}_f$ ont un unique point d'intersection $M$ distinct de l'origine.
On veut résoudre l’équation $f(x)=ax \iff x\text{e}^{-x}=ax \iff x\text{e}^{-x}-ax=0\iff x\left(\text{e}^{-x}-a\right)=0$
Un produit de facteurs est nul si, et seulement si, un de ses facteurs au moins est nul.
Donc $x=0$ ou $\text{e}^{-x}-a=0$
Or $\text{e}^{-x}-a=0\iff \text{e}^{-x}=a \iff -x=\ln a \iff x=-\ln a$
La droite $D_a$ et la courbe $\mathscr{C}_f$ ont donc un unique point d’intersection distinct de l’origine d’abscisse $x_M=-\ln a$.

On admet dans la suite de l'exercice que le point $M$ a pour abscisse $x_M = - \ln a$ et que la courbe $\mathcal{C}_f$ est située au-dessus de la droite $D_a$ sur l'intervalle $[0~;~- \ln (a)]$.

1. Montrer que $\mathcal{H}(a) = a \ln (a) - \frac{1}{2}a(\ln (a))^2 + 1 - a$.
$\mathscr{H}_a$ est l’aire du domaine compris entre la droite $D_a$, la courbe $\mathscr{C}_f$ et les droites d’équation $x=0$ et $x=-\ln a$.
Par conséquent :
$\begin{align*} \mathscr{H}_a&=\displaystyle \int_0^{-\ln a} \left(f(x)-ax\right) \;dx \\
&=\left[(-x-1)\text{e}^{-x}-\dfrac{ax^2}{2}\right]_0^{-\ln a} \\
&=\left(\ln a-1\right)\text{e}^{\ln a}-\dfrac{a\left(\ln a\right)^2}{2}-(-1)\text{e}^0 \\
&=\left(\ln a-1\right)\times a-\dfrac{1}{2}a\left(\ln a\right)^2+1\\
&=a\ln a-a-\dfrac{1}{2}a\left(\ln a\right)^2+1\\
&=a\ln a-\dfrac{1}{2}a\left(\ln a\right)^2+1-a
\end{align*}$

2. Soit la fonction $\mathcal{H}$ définie sur $]0~;~1]$ par $\mathcal{H}(x) = x \ln (x) - \frac{1}{2}x(\ln (x))^2 + 1 - x$. On admet que $\mathcal{H}$ est dérivable sur $]0~;~1] $ et que son tableau de variations correspond à celui qui est proposé ci-dessous.
   
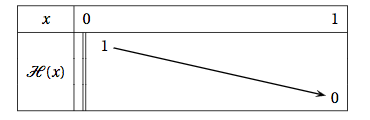
     Justifier qu'il existe un unique réel $\alpha \in ]0~;~1[$ tel que $\mathcal{H}(\alpha) = 0,5$.
La fonction $\mathscr{H}$ est continue (car dérivable) sur l’intervalle $]0;1]$ et strictement décroissante sur cet intervalle.
De plus $\mathscr{H}(0)=1>0,5$ et $\mathscr{H}(1)=0<0,5$. Or $0,5\in]0;1[$.
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) l’équation $\mathscr{H}(x)=0,5$ possède une unique solution sur l’intervalle $]0;1[$.
$\quad$
3. On considère l'algorithme présenté ci-dessous. $$\begin{array}{|lc|}\hline \text{VARIABLES } : &A, B \text{ et } C \text{ sont des nombres };\\ & p \text{ est un entier naturel }.\\ \text{ INITIALISATION } : & \text{ Demander la valeur de } p\\ & A \text{ prend la valeur } 0\\ &B \text{ prend la valeur } 1\\ \text{ TRAITEMENT } : & \text{Tant que } B - A > 10^{-p}\\ &\hspace{0.25cm} \begin{array}{|l} C \text{ prend la valeur } (A + B)/2\\ \text{Si } \mathcal{H}(C) > 0,5\\ \hspace{0.5cm} \begin{array}{|l} \text{ Alors } A \text{ prend la valeur de }C\\ \text{ Sinon }B \text{ prend la valeur de } C\\ \end{array}\\ \text{ Fin de la boucle Si } \\ \end{array}\\ &\text{ Fin de la boucle Tant que }\\ \text{SORTIE } : &\text{Afficher } A \text{ et } B.\\ \hline \end{array} $$ Que représentent les valeurs $A$ et $B$ affichées en sortie de cet algorithme ?
Les valeurs $A$ et $B$ sont, respectivement, un minorant et un majorant de $\alpha$ d’amplitude inférieure ou égale à $10^{-p}$.

4. Donner un encadrement d'amplitude $0,01$ de $\alpha$.
A l’aide de la calculatrice, on obtient l’encadrement $0,06< \alpha<0,07$ d’amplitude $0,01$.