Dérivées
Nombre dérivé
Remarque En physique, on notera souvent $\displaystyle f'(x_0)=\dfrac{df}{dx}(x_0)$.
Exemple
Soit $f:\mathbb{R}\rightarrow\mathbb{R}, x\mapsto x^2$. Pour tout $x\in\mathbb{R}$ et $h\neq 0$, le taux d'accroissement de $f$ est \[\tau_{x,h}f=\dfrac{(x+h)^2-x^2}h=\dfrac{2xh+h^2}h=2x+h\text{ donc } \displaystyle\lim_{h\to 0}\tau_{x,h}=2x=f'(x)\] Exemple
Montrer que $f:[0;+\infty[\to\mathbb{R}, \sqrt{x}$ n'est pas dérivable en $0$.Exemple
Montrer que $g:[0;+\infty[\to\mathbb{R}, x\mapsto x\sqrt{x}$ est dérivable en $0$. Calculer $g'(0)$.
Propriété Soit $f$ une fonction définie sur un intervalle ouvert $I$ et $x\in I$. Il existe une fonction $r$ et deux réels $a$ et $b$ tels que $\displaystyle\lim_{h\to 0}r(h)=0$ et $f(x+h)=b+ha+hr(h)$ si et seulement si $f$ est dérivable en
$x_0$. On a alors $f(x_0)=b$ et $f'(x_0)=a$.
Preuve
Si une telle fonction $r(h)$ existe, on a $f(x_0)=b$ en faisant tendre $h$ vers $0$. Ainsi, $r(h)=\tau_{x_0,h}-a$. Comme la limite en $0$ de $r(h)$ est nulle, $f$ est dérivable en $x_0$ et $f'(x_0)=a$.
Réciproquement, si $f$ est dérivable en $x_0$, la fonction définie par $r(h)=\tau_{x_0,h}-f'(x_0)$ possède les deux propriétés attendues.
Exemple
Soit $v:x\mapsto x^n$. Développer $v(x+h)$ à l'aide du binôme de Newton. Écrire $v(x+h)$ sous la forme $v(x+h)=v(x)+hb+hr(h)$ et en déduire $v'(x)$.
Interprétations
Interprétation géométrique
Soit $f$ une fonction définie sur $I$ et dérivable en $x_0\in I$. On note $\mathcal{ C}$ sa courbe représentative dans un repère orthonormé. On note $M_0$ le point de $\mathcal{ C}$ d'abscisse $x_0$ et $M_h$ le point de $\mathcal{ C}$d'abscisse $x_0+h$.
Le coefficient directeur de la sécante $S_h=(M_0M_h)$ à la courbe $\mathcal{ C}$ est le taux d'accroissement $\tau_{x_0,h}f$.
Lorsque $h$ tend vers $0$, la position limite de $M_h$ est celle du point $M$ et la position limite de la sécante $S_h$ est la tangente $T_{x_0}$ à $\mathcal C$ au point d'abscisse $x_0$.
Le coefficient directeur de cette tangente est $f'(x_0)$, la limite des coefficients directeurs des sécantes.
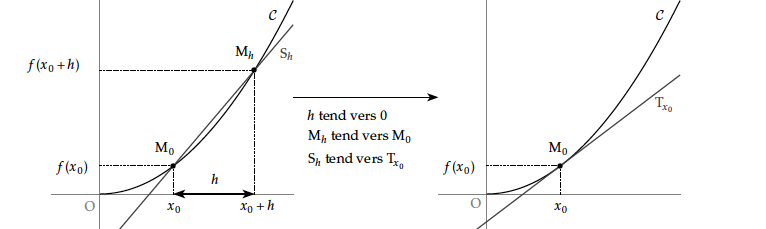
Soit $f$ une fonction définie sur $I$ et dérivable en $x_0\in I$. On note $\mathcal{ C}$ sa courbe représentative dans le plan muni d'un repère orthonormé $\left(\text{O},\vec{j},\vec{j},\vec{k}\right)$.
La tangente à la courbe $\mathcal C$ au point d'abscisse $x_0$ est la droite $T_{x_0}$ d'équation \[y=f'(x_0)(x-x_0)+f(x_0).\] En particulier, le coefficient directeur de cette tangente est le nombre $f'(x_0)$.
Exemple
Équation de la tangente à $\mathcal {P}:y=f(x)$ (où $f:x\mapsto x^2$) au point $A(1,1)$ ?
Remarque Si la limite en $x_0$ du taux d'accroissement $\tau_{x_0,h}f$ est $+\infty$ ou $-\infty$, la courbe $\mathcal C$ admet en $x_0$ une tangente verticale d'équation $x=x_0$.
Exemple
Montrer que la courbe de $x\mapsto\sqrt x$ admet une tangente verticale à l'origine. l
Interprétation cinétique
Soit $x(t)$ la position d'un mobile en mouvement rectiligne sur un axe gradué, en fonction du temps $t$. Le taux d'accroissement $\tau_{t_0,h}x$ représente la vitesse moyenne du mobile entre $t_0$ et $t_0+h$, alors que $x'(t)$ est la vitesse instantanée du mobile au temps $t$.
Interprétation numérique
Exemple
Soit $u:x\mapsto \dfrac 1x$. Donner $u'(1)$, une approximation de $\dfrac1{1+h}$ puis de $\dfrac{1}{1{,}001}$
- 1
- 2
- 3
- 4
- Toutes les pages
- Vues: 14430
