Introduction
Des arguments de type probabiliste peuvent être avancés et pris en compte dans les cours de justice. Un accusé d'origine mexicaine, condamné pour vol et tentative de viol dans un comté du sud du Texas attaqua le jugement sous le motif que la désignation des jurés dans l'Etat du Texas était discriminatoire pour les Américains d'origine mexicaine. Son argument était que ceux-ci n'étaient pas suffisamment représentés dans les jurys populaires.
Attendu de la Cour Suprême des Etats-Unis (affaire Castaneda contre Partida) :
« Si les jurés étaient tirés au hasard dans l'ensemble de la population, le nombre d'américains mexicains dans l'échantillon pourrait alors être modélisé par une distribution binomiale $\ldots$
Etant donné que 79,1 % de la population est mexico-américaine, le nombre attendu d'américains mexicains parmi les 870 personnes convoquées en tant que grands jurés pendant la période de 11 ans est approximativement 688. Le nombre observé est 339.
Bien sûr, dans n'importe quel tirage considéré, une certaine fluctuation par rapport au nombre attendu est prévisible. Le point essentiel cependant, est que le modèle statistique montre que les résultats d'un tirage au sort tombent vraisemblablement dans le voisinage de la valeur attendue?
La mesure des fluctuations prévues par rapport à la valeur attendue est l'écart type, défini pour la distribution binomiale comme la racine carrée de la taille de l'échantillon (ici 870) fois la probabilité de sélectionner un américain mexicain (ici 0,791) fois la probabilité de sélectionner un non américain mexicain (ici 0,209)?
Ainsi, dans ce cas, l'écart type est approximativement de 12.
En règle générale pour de si grands échantillons, si la différence entre la valeur attendue et le nombre observé est plus grand que deux ou trois écarts types, alors l'hypothèse que le tirage du jury était au hasard serait suspect à un spécialiste des sciences humaines.
Les données sur 11 années reflètent ici une différence d'environ 29 écarts types. Un calcul détaillé révèle qu'un éloignement aussi important de la valeur attendue se produirait avec moins d'une chance sur $10^{140}$. »
Questions
- Définir la variable aléatoire qui, dans cette situation, suit une loi binomiale.
- Quels sont les paramètres de la loi binomiale ?
- A quel calcul correspond la valeur 688 ?
- Effectuer le calcul de l'écart-type
A quoi correspond la « différence de 29 écarts types »?
- A quel évènement correspond la probabilité $10^{-140}$ ?
- La constitution des jurys est-elle aléatoire ?
La population du Texas est assez grande pour que les 870 jurés soient assimilés à un échantillon de 870 boules tirées avec remise dans une urne qui en contient 1000 dont 791 vertes représentent les personnes d'origine mexicaine, les autres boules sont rouges.
La probabilité d'obtenir 339 boules vertes ou moins est égale à $\displaystyle\sum_{k=0}^{339}\binom{870}{k}\times 0,791^k\times \left (1-0,791\right )^{870-k}$.
Les calculatrices classiques ne permettent pas d'effectuer ce calcul, à cause d'un dépassement de capacité au moment du calcul des coefficients binomiaux.
Il semble opportun « d'approcher »la loi $\mathcal{B}\left (870;0,791\right )$ par une loi permettant de calculer $P\left ([0;339]\right )$ plus facilement.
La première opération à effectuer semble être de « centrer »$X_n$, suivant la loi $\mathcal{B}(870;0,791)$, autour de 0.
Observation du diagramme associé à la variable aléatoire $Y_n=X_n-np$
Consulter le fichier binomiale n p .ggb
Rappels de 1 S $a$ et $b$ étant des réels fixés, $X$ désignant une variable aléatoire,
- $E(aX+b)=aE(X)$
- $V(a.X+b)=a^2V(X)$
$E(Y_n)=E(1.X_n+\left (-np\right ))=1.E(X_n)+\left (-np\right )=np-np=0$
$V(Y_n)=1^2V(X_n)=V(X_n)=npq$.
$Y_n$ est dite centrée.
La deuxième opération à effectuer semble être de « réduire »l'étalement de $Y_n$ autour de 0.
Observation du diagramme associé à la variable aléatoire $Z_n=\dfrac{Y_n}{\sqrt{npq}}=\dfrac{X_n-np}{\sqrt{npq}}$
$E(Z_n)=\dfrac{1}{\sqrt{npq}}E(Y_n)=0$.\\ $V(Z_n)=\left (\dfrac{1}{\sqrt{npq}}\right )^2V(Y_n)=\dfrac{1}{npq}\times npq=1$.
$Z_n$ est dite centrée et réduite.
Consulter le fichier centrer et réduire une binomiale.ggb
Conjecture
Après avoir remplacé $Z_n$ par une loi continue dont la fonction densité est une fonction en escalier, on observe que cette dernière loi peut être elle-même approchée par une loi continue appelée loi normale $\mathcal{N}(0;1)$.
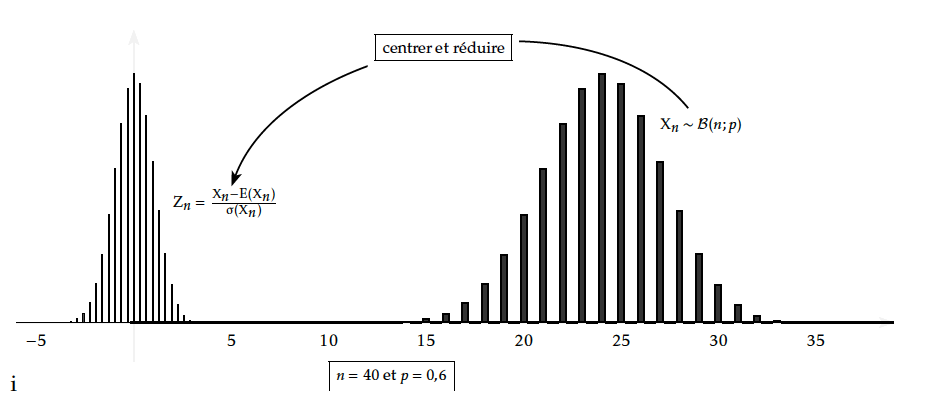
Théorème de Moivre-Laplace (admis)
Soit $p\in]0;1[$. Pour tout entier $n\geq 1$, soit $X_n\sim\mathcal B(n;p)$ et la variable aléatoire centrée réduite $Z_n=\dfrac{X_n-np}{\sqrt{npq}} $ correspondante .
Alors $Z_n$ converge en loi vers la variable aléatoire $X$ qui suit la loi $\mathcal{N}(0;1)$.
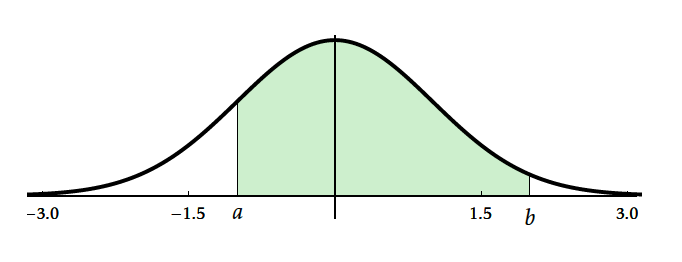
Autrement dit quels que soient $a$ et $b$ deux réels, $a\leq b$. On a \[ \displaystyle\lim_{n\to+\infty} P(a\leq Z_n \leq b)=P(a\leq X\leq b)=\displaystyle\int_a^bf(x)\;dx \quad\text{où}\quad f(x)=\dfrac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2} } \text{ pour tout } x \in \mathbb{R} \]
Ce théorème signifie que, pourvu que $n$ soit suffisamment grand, on peut estimer $P(a\leq Z_n\leq b)$ par $P(a\leq X\leq b)$.
</>Il est admis, voir le TP 8 pour une approche empirique.
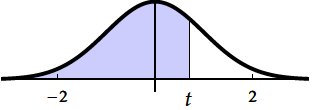
La loi $\mathcal{N}(0;1)$
La loi normale centrée réduite est caractérisée par la densité de probabilité~: $\displaystyle { f (x) = \dfrac{1}{\sqrt {2\pi }} e^{-x^2/2}. }$
Extraits de la table associée à la loi normale centrée réduite ${\cal N} (0, 1)$.
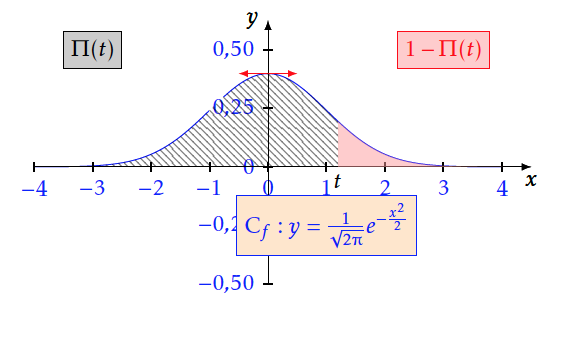
$$ \Pi (t) = P \big( T \leq t\big) = \int _{-\infty }^t f (x) \, {\rm d}x =0,5+\int _{0 }^t f (x) \, {\rm d}x \qquad \qquad $$ $f$ est continue sur $\mathbb{R}$, donc $\Pi'(t)=f(t)$.
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline & t&& 0,00&& 0,01&& 0,02&& 0,03&& 0,04&& 0,05&& 0,06&& 0,07&& 0,08&& 0,09 \\ \hline & 0,0&& 0,500\, 0&& 0,504\, 0&& 0,508\, 0&& 0,512\, 0&& 0,516\, 0&& 0,519\, 9&& 0,523\, 9&& 0,527\, 9&& 0,531\, 9&& 0,535\, 9 \\ \hline & 0,1&& 0,539\, 8&& 0,543\, 8&& 0,547\, 8&& 0,551\, 7&& 0,555\, 7&& 0,559\, 6&& 0,563\, 6&& 0,567\, 5&& 0,571\, 4&& 0,575\, 3 \\\hline & 0,2&& 0,579\, 3&& 0,583\, 2&& 0,587\, 1&& 0,591\, 0&& 0,594\, 8&& 0,598\, 7&& 0,602\, 6&& 0,606\, 4&& 0,610\, 3&& 0,614\, 1 \\\hline & 0,3&& 0,617\, 9&& 0,621\, 7&& 0,625\, 5&& 0,629\, 3&& 0,633\, 1&& 0,636\, 8&& 0,640\, 6&& 0,644\, 3&& 0,648\, 0&& 0,651\, 7 \\\hline & 0,4&& 0,655\, 4&& 0,659\, 1&& 0,662\, 8&& 0,666\, 4&& 0,670\, 0&& 0,673\, 6&& 0,677\, 2&& 0,680\, 8&& 0,684\, 4&& 0,687\, 9 \\\hline & 0,5&& 0,691\, 5&& 0,695\, 0&& 0,698\, 5&& 0,701\, 9&& 0,705\, 4&& 0,708\, 8&& 0,712\, 3&& 0,715\, 7&& 0,719\, 0&& 0,722\, 4 \\\hline & 0,6&& 0,725\, 7&& 0,729\, 1&& 0,732\, 4&& 0,735\, 7&& 0,738\, 9&& 0,742\, 2&& 0,745\, 4&& 0,748\, 6&& 0,751\, 7&& 0,754\, 9 \\\hline & 0,7&& 0,758\, 0&& 0,761\, 1&& 0,764\, 2&& 0,767\, 3&& 0,770\, 3&& 0,773\, 4&& 0,776\, 4&& 0,779\, 3&& 0,782\, 3&& 0,785\, 2 \\\hline & 0,8&& 0,788\, 1&& 0,791\, 0&& 0,793\, 9&& 0,796\, 7&& 0,799\, 5&& 0,802\, 3&& 0,805\, 1&& 0,807\, 8&& 0,810\, 6&& 0,813\, 3 \\\hline & 0,9&& 0,815\, 9&& 0,818\, 6&& 0,821\, 2&& 0,823\, 8&& 0,826\, 4&& 0,828\, 9&& 0,831\, 5&& 0,834\, 0&& 0,836\, 5&& 0,838\, 9 \\\hline & & & & & & & & & & & \\\hline & 1,0&& 0,841\, 3&& 0,843\, 8&& 0,846\, 1&& 0,848\, 5&& 0,850\, 8&& 0,853\, 1&& 0,855\, 4&& 0,857\, 7&& 0,859\, 9&& 0,862\, 1 \\\hline & 1,1&& 0,864\, 3&& 0,866\, 5&& 0,868\, 6&& 0,870\, 8&& 0,872\, 9&& 0,874\, 9&& 0,877\, 0&& 0,879\, 0&& 0,881\, 0&& 0,883\, 0 \\\hline & 1,2&& 0,884\, 9&& 0,886\, 9&& 0,888\, 8&& 0,890\, 6&& 0,892\, 5&& 0,894\, 3&& 0,896\, 2&& 0,898\, 0&& 0,899\, 7&& 0,901\, 5\\\hline & 1,3&& 0,903\, 2&& 0,904\, 9&& 0,906\, 6&& 0,908\, 2&& 0,909\, 9&& 0,911\, 5&& 0,913\, 1&& 0,914\, 7&& 0,916\, 2&& 0,917\, 7\\\hline & 1,4&& 0,919\, 2&& 0,920\, 7&& 0,922\, 2&& 0,923\, 6&& 0,925\, 1&& 0,926\, 5&& 0,927\, 9&& 0,929\, 2&& 0,930\, 6&& 0,931\, 9\\\hline & 1,5&& 0,933\, 2&& 0,934\, 5&& 0,935\, 7&& 0,937\, 0&& 0,938\, 2&& 0,939\, 4&& 0,940\, 6&& 0,941\, 8&& 0,942\, 9&& 0,944\, 1\\\hline & 1,6&& 0,945\, 2&& 0,946\, 3&& 0,947\, 4&& 0,948\, 4&& 0,949\, 5&& 0,950\, 5&& 0,951\, 5&& 0,952\, 5&& 0,953\, 5&& 0,954\, 5\\\hline & 1,7&& 0,955\, 4&& 0,956\, 4&& 0,957\, 3&& 0,958\, 2&& 0,959\, 1&& 0,959\, 9&& 0,960\, 8&& 0,961\, 6&& 0,962\, 5&& 0,963\, 3\\\hline & 1,8&& 0,964\, 1&& 0,964\, 9&& 0,965\, 6&& 0,966\, 4&& 0,967\, 1&& 0,967\, 8&& 0,968\, 6&& 0,969\, 3&& 0,969\, 9&& 0,970\, 6\\\hline & 1,9&& 0,971\, 3&& 0,971\, 9&& 0,972\, 6&& 0,973\, 2&& 0,973\, 8&& 0,974\, 4&& 0,975\, 0&& 0,975\, 6&& 0,976\, 1&& 0,976\, 7\\\hline & & & & & & & & & & &\\\hline & 2,0&& 0,977\, 2&& 0,977\, 8&& 0,978\, 3&& 0,978\, 8&& 0,979\, 3&& 0,979\, 8&& 0,980\, 3&& 0,980\, 8&& 0,981\, 2&& 0,981\, 7\\\hline & 2,1&& 0,982\, 1&& 0,982\, 6&& 0,983\, 0&& 0,983\, 4&& 0,983\, 8&& 0,984\, 2&& 0,984\, 6&& 0,985\, 0&& 0,985\, 4&& 0,985\, 7\\\hline & 2,2&& 0,986\, 1&& 0,986\, 4&& 0,986\, 8&& 0,987\, 1&& 0,987\, 5&& 0,987\, 8&& 0,988\, 1&& 0,988\, 4&& 0,988\, 7&& 0,989\, 0\\\hline & 2,3&& 0,989\, 3&& 0,989\, 6&& 0,989\, 8&& 0,990\, 1&& 0,990\, 4&& 0,990\, 6&& 0,990\, 9&& 0,991\, 1&& 0,991\, 3&& 0,991\, 6\\\hline & 2,4&& 0,991\, 8&& 0,992\, 0&& 0,992\, 2&& 0,992\, 5&& 0,992\, 7&& 0,992\, 9&& 0,993\, 1&& 0,993\, 2&& 0,993\, 4&& 0,993\, 6\\\hline & 2,5&& 0,993\, 8&& 0,994\, 0&& 0,994\, 1&& 0,994\, 3&& 0,994\, 5&& 0,994\, 6&& 0,994\, 8&& 0,994\, 9&& 0,995\, 1&& 0,995\, 2\\\hline & 2,6&& 0,995\, 3&& 0,995\, 5&& 0,995\, 6&& 0,995\, 7&& 0,995\, 9&& 0,996\, 0&& 0,996\, 1&& 0,996\, 2&& 0,996\, 3&& 0,996\, 4\\\hline & 2,7&& 0,996\, 5&& 0,996\, 6&& 0,996\, 7&& 0,996\, 8&& 0,996\, 9&& 0,997\, 0&& 0,997\, 1&& 0,997\, 2&& 0,997\, 3&& 0,997\, 4\\\hline & 2,8&& 0,997\, 4&& 0,997\, 5&& 0,997\, 6&& 0,997\, 7&& 0,997\, 7&& 0,997\, 8&& 0,997\, 9&& 0,997\, 9&& 0,998\, 0&& 0,998\, 1\\\hline & 2,9&& 0,998\, 1&& 0,998\, 2&& 0,998\, 2&& 0,998\, 3&& 0,998\, 4&& 0,998\, 4&& 0,998\, 5&& 0,998\, 5&& 0,998\, 6&& 0,998\, 6\\\hline \end{array} $$
Table pour les grandes valeurs de $ t$
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline & t && 3,0&& 3,1&& 3,2&& 3,3&& 3,4&& 3,5&& 3,6&& 3,8&& 4,0&& 4, 5 \\ \hline & \Pi (t)&& 0,998\, 65&& 0,999\, 04&& 0,999\, 31&& 0,999\, 52&& 0,999\, 66&& 0,999\, 76&& 0,999\, 841&& 0,999\, 928&& 0,999\, 968&& 0,999\, 997\\ \hline \end{array}$$
Nota : La table donne les valeurs de $\Pi (t)$ pour $t$ positif.
Lorsque $t$ est négatif, il faut prendre le complément à l'unité de la valeur lue dans la table pour la valeur absolue de $t$.
Exemple :
pour $t=1,37$ ;$ \Pi (1,37)=0,914\, 7$
pour $t=-1,37$ ;$ \Pi (-1,37)=1-0,914\, 7=0,085\, 3$
Propriétés de la loi $\mathcal{N}(0;1)$
Des propriétés faciles à mémoriser ...
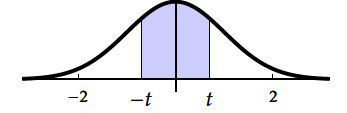
$$\begin{array}{|c|c|c| }P(X\leq t)=\Pi(t) & 1-P(X\leq t)=P(X\leq -t)=\Pi(-t) & P(-t\leq X\leq t) =\displaystyle\int_{-t}^t f(x)\;dx \\ & 1-\Pi(t)=\Pi(-t) & P(X\leq t)-P(X\leq -t)=\Pi(t)-\Pi(-t) \\ & & P(X\leq t)-P(X\leq -t)=\Pi(t)-\left [1-\Pi(t)\right ] \\ & & P(-t\leq X\leq t)=2\Pi(t)-1 \\ \end{array}$$
Espérance et variance
La fonction $x\mapsto e^{-\frac{x^2}{2}}$ ne peut pas se mettre sous la forme $u'e^{u}$ .
alors que $xe^{-\frac{x^2}{2}}=-\underbrace{\left (-x\right ) e^{-\frac{x^2}{2}}}_{\text{ Je reconnais } u'e^u }$
Donc $\displaystyle\int _a^b xe^{-\frac{x^2}{2}}\;dx =\left [-e^{-\frac{x^2}{2}}\right ]_a^b=-e^{-\frac{b^2}{2}}+e^{-\frac{a^2}{2}}$, avec $\displaystyle\lim_{a\to -\infty}e^{-\frac{a^2}{2}}=0$ et $\displaystyle\lim_{b\to +\infty}e^{-\frac{b^2}{2}}=0$
Donc $\displaystyle\lim_{a\to -\infty \\ b\to +\infty}\int _a^b xe^{-\frac{x^2}{2}}\;dx=0$ et ainsi $E(X)=0\times \dfrac{1}{\sqrt{2\pi}}=0$.
On admet $V(X)=1$ , donc $\sigma(X)=1$.
Si $X$ suit la loi normale $\mathcal{N}(0;1)$ alors $E(X)=0; V(X)=1$ et $\sigma(X)=1$
Un théorème
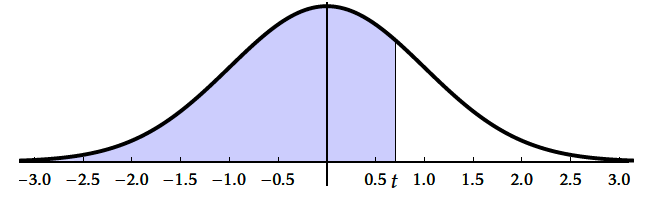
On consid ère la fonction $\Pi$ définie sur $\mathbb{R}^+$ par : $$\Pi\left(t\right)=\displaystyle\int_{-\infty}^t\dfrac{1}{\sqrt{2\pi{}}}e^{-\frac{x^2}{2}}dx=0.5+\int_{0}^t\frac{1}{\sqrt{2\pi{}}}e^{-\frac{x^2}{2}}dx$$ Pour tout réel $\alpha{}$ de ]0 ; 1[ , il existe un seul réel positif $u_{\alpha}$ tel que $P\left(-u_{\alpha}\leq X\leq u_{\alpha}\right)=1-\alpha$.
Déjà comme $\alpha \in ]0;1[$; on a $1-\alpha \in \left ]0;1\right[$.
Il s'agit donc ici de déterminer un antécédent $ u_{\alpha}$ du nombre $1-\alpha$, on utilise ici le théorème de la bijection !
La fonction $f:x\mapsto \frac{1}{\sqrt{2\pi{}}}e^{-\frac{x^2}{2}}$ est continue sur $\mathbb{R}$, donc la fonction $a$ définie sur $\mathbb{R}^+$ par $a\left(t\right)=\displaystyle\int_{-t}^t\frac{1}{\sqrt{2\pi{}}}e^{-\frac{x^2}{2}}dx$ est dérivable sur $\mathbb{R}^+$, en effet la fonction $F$ définie sur $\mathbb{R}^+$ par $F\left(t\right)=\displaystyle\int_{0}^t\frac{1}{\sqrt{2\pi{}}}e^{-\frac{x^2}{2}}dx$ est la primitive de $f$ sur $\mathbb{R}^+$ qui s'annule en 0.
Ainsi $F$ est dérivable sur $\mathbb{R}^+$ et $F'(x)=f(x)$,
On a ensuite $a\left(t\right)=\displaystyle\int_{-t}^t\frac{1}{\sqrt{2\pi{}}}e^{-\frac{x^2}{2}}dx=2\displaystyle\int_{0}^t\frac{1}{\sqrt{2\pi{}}}e^{-\frac{x^2}{2}}dx=2\;F(t)$
En dérivant, il vient : $a'(t)= 2\;F'(t)=2\;f(t)$ la fonction exponentielle étant strictement positive sur $\mathbb{R}$, on a donc :
$\forall t \in \mathbb{R}^+; a'(t)>0$
Par ailleurs $\lim\limits_{t\rightarrow +\infty}F(t)=\dfrac{1}{2}$, donc $\lim\limits_{t\rightarrow +\infty}a(t)=1$
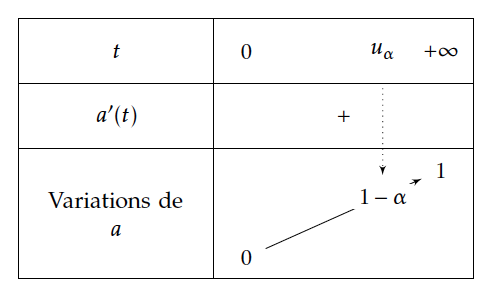
$a$ est donc continue car dérivable , strictement croissante sur $[0;+\infty[$,
donc $a$ réalise une bijection de $[0;+\infty[$ sur $\left[a(0);\lim\limits_{t\rightarrow +\infty}a(t)\right[$ soit sur $\left[0;1\right[$.
Or $1-\alpha \in \left [0;1\right[$,\enc{ donc l'équation $a(t)=1-\alpha$ a une solution unique $u_{\alpha}$ dans $[0;+\infty[$.}
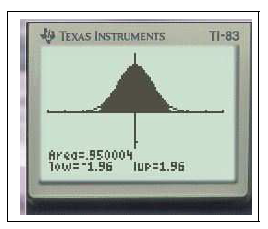
- Pour $\alpha =0,05$ : $2\Pi(t)-1=0,05$ équivaut à $\Pi(t)=\dfrac{1,95}{2}=0,975\approx \Pi(1,96)$ \enc{$u_{0,05}\approx 1,96$}
- Pour $\alpha =0,01$ : $2\Pi(t)-1=0,01$ équivaut à $\Pi(t)=\dfrac{1,99}{2}=0,995\approx \Pi(2,58)$ \enc{$u_{0,01}\approx 2,58$}
Les lois $\mathcal{N}(\mu;\sigma^2)$ d'espérance $\mu >0$ et d'écart-type $\sigma>0$
Définition
$X$ suit une loi $N(\mu, \sigma ^2 )$ si $T = \frac{ X - \mu }{\sigma }$ suit une loi $ N(0,1)$ On admet $E(X)=\mu ; V(X)= \sigma^2$ et $\sigma(X)=\sigma$.
La loi $\mathcal{N}(\mu;\sigma^2)$ possède une densité $f_{\mu,\sigma}$ définie sur $\mathbb{R}$ par $f_{\mu,\sigma}(x)=\frac{1}{\sigma\sqrt { 2\Pi }}e^{ - \frac{ 1 }{2}\left (\dfrac{x-\mu}{\sigma} \right )^2}$
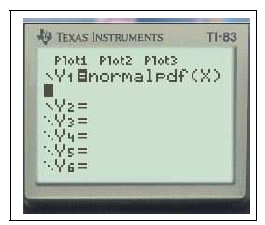
Sur la calculatrice $Y_1=normalFdp(X,\mu,\sigma)$ On a $P(a\leq X_{\mu,\sigma}\leq b)\approx normalFr\text{é}p(a,b,\mu,\sigma)$
Un résultat à savoir
Lorsque $X_{\mu,\sigma}$ suit la loi $\mathcal{N}(\mu;\sigma^2)$ :
- $P(\mu-\sigma\leq X_{\mu,\sigma}\leq \mu+\sigma)\approx 0,683$
- $P(\mu-2\sigma\leq X_{\mu,\sigma}\leq \mu+2\sigma)\approx 0,954$
- $P(\mu-3\sigma\leq X_{\mu,\sigma}\leq \mu+3\sigma)\approx 0,997$
$X_{\mu,\sigma} \in\left [\mu-3\sigma;[\mu-3\sigma\right ] $ équivaut à $-3\leq \dfrac{X-\mu}{\sigma}\leq 3$ ( car $\sigma>0$)
- $P\left (X_{\mu,\sigma} \in\left [\mu-3\sigma; \mu+3\sigma\right ]\right ) =P\left (-3\leq \dfrac{X-\mu}{\sigma}\leq 3\right )=2\Pi(3)-1\approx 2\times0,998\,65-1=0,9973$.
$P\left (X_{\mu,\sigma} \in\left [\mu-3\sigma; \mu+3\sigma\right ]\right )\approx 0,99 $
- $P\left (X_{\mu,\sigma} \in\left [\mu-2\sigma; \mu+2\sigma\right ]\right ) =P\left (-2\leq \dfrac{X-\mu}{\sigma}\leq 2\right )=2\Pi(2)-1\approx 2\times0,9772-1=0,9544$.
$P\left (X_{\mu,\sigma} \in\left [\mu-2\sigma; \mu+2\sigma\right ]\right )\approx 0,95$
- $P\left (X_{\mu,\sigma} \in\left [\mu-\sigma; \mu+\sigma\right ]\right ) =P\left (-1\leq \dfrac{X-\mu}{\sigma}\leq 1\right )=2\Pi(1)-1\approx 2\times0,8413-1=0,6826$.
$P\left (X_{\mu,\sigma} \in\left [\mu-\sigma; \mu+\sigma\right ]\right )\approx 0,68 $
Retour sur l'exemple introductif
Soit $Y$ la variable aléatoire qui compte le nombre de boules vertes tirées lors des 870 tirages avec remise: $Y$ suit la loi $\mathcal{B}(870;0,791)$ d'espérance mathématique $870\times 0,791\approx 688$ et d'écart-type $\sqrt{870\times 0,791\times 0,209}\approx 12$.
$P(Y\leq 339)=P\left (\dfrac{Y- 688}{12}\leq \dfrac{339-688}{12}\right )\approx P\left (\dfrac{Y- 688}{12}\leq-29\right ).$
On approche $\dfrac{Y- 688}{12}$ par la loi $\mathcal{N}(0;1)$ donc $P(Y\leq 339)\approx \Pi(-29)\approx 0$.
On est contraint de remettre en cause le choix des jurés.
Soit $X_{688,12}$ une variable aléatoire suivant la loi normale $\mathcal{N}(688;12^2)$
$P(X_{688,12}\leq 339)\approx P\left (\dfrac{X_{688,12}- 688}{12}\leq -29\right )=\Pi(-29).$
Tout se passe comme si on approchait $Y$ par $X_{688,12}$.
Calculatrice
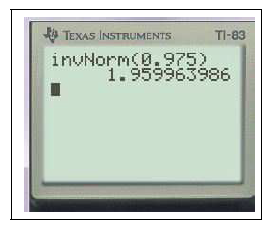
- Calcul de $u_{\alpha}$ :
2ndDISTR3FracNormale(0,975)EXE
$FracNormale(0,975)\approx 1,96$
- Fonction densité :
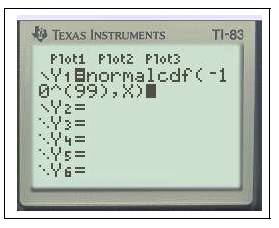
$Y_1=$normalFdp(X)graphezoom0:ZMinMax
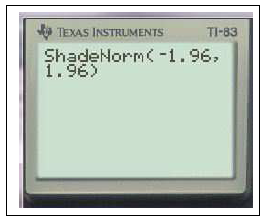
2ndDISTRDESSIN1:OmbreNorm(-1.96,1.96)
Dans les deux cas ci-dessus, on peut ajouter $\mu$ et $\sigma$ :
Par exemple pour afficher la densité de la loi normale $\mathcal{N}(2,1)$; on tape :
$Y_1=$normalFdp(X,2,1)graphezoom
- $\Pi(t)$:
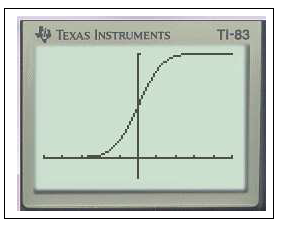
$Y_1=$normalFRép(-10,X)graphezoom
En effet on peut remarquer que $f(-10)\approx 7,7.10^{-23}$ ou encore avec un logiciel de calcul formel ( Maple) on obtient $\displaystyle\lim_{a\to -\infty}\int_a^{-10} f(x) \;dx\approx 7.10^{-24}$
- Pour la loi binomiale :
2ndDISTR0binomFdp(
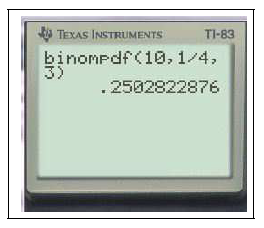
$binomFdp(10,0.25,3)\approx 0.25$
Ceci calcule $P(X=3)$ dans le cas où $X$ suit la loi binomiale $\mathcal{B}(10,0.25)$
2ndDISTR0binomFdp(
$binomFdp(10,0.25,3)\approx 0.25$
Ceci calcule $P(X=k)$ pour $k =3$ dans le cas où $X$ suit la loi binomiale $\mathcal{B}(10,0.25)$
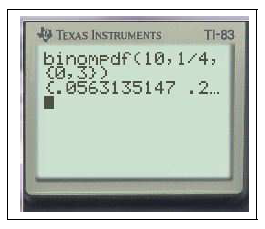
2ndDISTR0binomFdp(
$binomFdp(10,0.25)$ Ceci calcule la liste des probabilités $P(X=k)$ pour $k \in\{0,1,2,3,4,5,6,7,8,9,10\}$ dans le cas où $X$ suit la loi binomiale $\mathcal{B}(10,0.25)$
Cela fournit donc la loi de probabilité de cette variable aléatoire.
2ndDISTR0binomFRép(
$binomFR\text{é}p(10,0.25,3)\approx 0.78$
Ceci calcule la probabilité $P(X\leq 3)$ dans le cas où $X$ suit la loi binomiale $\mathcal{B}(10,0.25)$
2ndDISTR0binomFRép(
$binomFR\text{é}p(10,0.25)$
Ceci calcule la liste des $P(X\leq k)$( $0\leq k\leq 10$) dans le cas où $X$ suit la loi binomiale $\mathcal{B}(10,0.25)$
Exercice
Soit $X$ une variable aléatoire suivant $\mathcal{B}(10,0.25)$
Calculer de deux façons différentes $P(2\leq X\leq 7)$
Exercice
On lance indépendamment $400$ fois une pièce équilibrée. On note $X$ le nombre de résultats « face» et $\tilde X$ la variable aléatoire centrée réduite correspondante.
Montrer que $P(190\leq X\leq 220)= P(-1\leq \tilde X\leq 2)$. Estimer alors $ P(190\leq X\leq 220)$
Intervalle de fluctuation -Estimation
Un résultat préliminaire fondamental $\left (n\in \mathbb{N}^{\star}\right )$
On considère $X_n$ qui suit la loi $\mathcal{B}(n,p)$.
On pose $F_n=\dfrac{X_n}{n}$ et $Z_n=\dfrac{X_n-np}{\sqrt{npq}}=\dfrac{F_n-p}{\sqrt{\dfrac{pq}{n}}}.$
Alors les encadrements suivants sont équivalents : $\left ( \text{ car } \sqrt{\dfrac{pq}{n}}>0\right )$
$$-u_{\alpha}\leq Z_n\leq u_{\alpha}$$ $$-u_{\alpha}\leq \dfrac{F_n-p}{\sqrt{\dfrac{pq}{n}}}\leq u_{\alpha}$$ $$-u_{\alpha}.\sqrt{\dfrac{pq}{n}}\leq F_n-p\leq u_{\alpha}.\sqrt{\dfrac{pq}{n}}$$ $$\left | F_n-p\right |\leq u_{\alpha}.\sqrt{\dfrac{pq}{n}}$$ Cette dernière inégalité peut s'écrire de deux façons :
$$\begin{array}{c|c} p-u_{\alpha}.\sqrt{\dfrac{pq}{n}}\leq F_n\leq p+u_{\alpha}.\sqrt{\dfrac{pq}{n}} & F_n-u_{\alpha}.\sqrt{\dfrac{pq}{n}}\leq p \leq F_n+u_{\alpha}.\sqrt{\dfrac{pq}{n}}\\ F_n \in I_n & text{ pas d'intervalle} \\ p \text{ est connue : Fluctuation} & p \text{ est inconnue : Estimation} \\ \end{array}$$
Intervalle de fluctuation: $p$ est connue $\left (n\in \mathbb{N}^{\star}\right )$.
$P\left (F_n\in I_n\right )=P\left (-u_{\alpha}\leq Z_n\leq u_{\alpha}\right )$ dont la limite en $+\infty$ est $P\left (-u_{\alpha}\leq X_{0,1}\leq u_{\alpha}\right )=1-\alpha$.
Pour $\alpha\approx 0,05$ on obtient $\tilde{I_n}=\left [p-1,96\sqrt{\dfrac{pq}{n}};p+1,96\sqrt{\dfrac{pq}{n}}\right ].$
Exemple
Cours de 2nde :
$$P\left( p-\dfrac{1}{\sqrt n}\leq F_n\leq p+\dfrac{1}{\sqrt n}\right )\geq P\left (F_n\in I_n\right )$$ $$ \text{ dès que, successivement:}$$ $$I_n\subset\left[ p-\dfrac{1}{\sqrt n}; p+\dfrac{1}{\sqrt n}\right]$$ $$ \text{ à peu près }\; 1,96\dfrac{\sqrt{pq}}{\sqrt{n}} \leq \dfrac{1}{\sqrt{n}} $$ $$\sqrt{pq}\leq \dfrac{1}{1,96} \; (\text{ dans } \; \mathbb{R}^+)$$ $$pq\leq \left (\dfrac{1}{1,96}\right )^2 \; \text{ avec } \; \left (\dfrac{1}{1,96}\right )^2\approx 0,2603$$ $$p(1-p)=pq\leq 0,26$$ $$\text{Or si on pose }\;V(p)=p(1-p)=-p^2+p \;\text{ pour tout } p \in [0;1] \; \text{on a } \;V'(p)=-2p+1$$ $$\text{d'où le tableau de variation de } \;V\; \text{ sur } [0;1]:$$
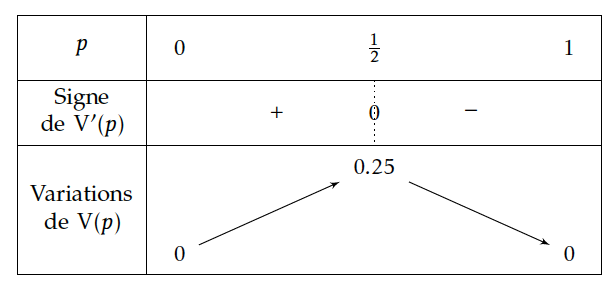
Donc $V(p)\leq 0,26$ sur $[0;1]$
Il résulte de $\displaystyle\lim_{n\rightarrow +\infty}P\left (F_n\in I_n\right )=0,95$ que pour $n$ « suffisamment grand »( $n\geq 30$):
$$P\left( p-\dfrac{1}{ \sqrt n}\leq F_n\leq p+\dfrac{1}{\sqrt n}\right )\approx 0,95$$
Estimation: $p$ est inconnue.
Le programme
$$\text{pour } n \text{ « suffisamment grand : »} P\left( p-\dfrac{1}{ \sqrt n}\leq F_n\leq p+\dfrac{1}{\sqrt n}\right )\geq0,95$$ $$\text{ c'est-à-dire : } P\left (\left | F_n-p\right |\leq \dfrac{1}{\sqrt{n}}\right )\geq 0,95$$ $$\text{ autrement dit, au niveau de confiance de } 0,95, p \text{ peut être estimée avec la précision } \dfrac{1}{\sqrt{n}} $$ $$\text{ par la fréquence } f \text{ associée à un échantillon de taille }n \text{( « suffisamment grand(e)»).}$$
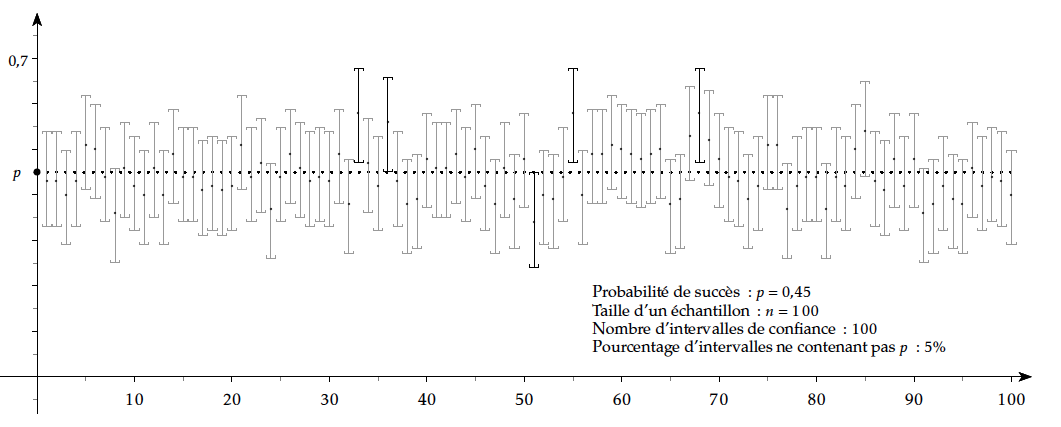
Avant le second tour d'une élection présidentielle, on effectue deux sondages sur des échantillons représentatifs de la population.
On ne retient que les suffrages exprimés, c'est-à -dire les personnes qui ont l'intention de voter pour l'un ou l'autre des candidats.
- le premier sondage concerne 1 003 personnes qui votent à 53,1 % pour le candidat A .
- le seconde sondage concerne 9 851 personnes qui votent à 51,2 % pour le candidat A .
Lequel de ces sondages permet d'affirmer, au seuil de confiance de 95 %, que le candidat A va l'emporter ?
Cas général
$$\text{ pour } n \text{« suffisamment grand »: } P\left( p-u_{\alpha}.\sqrt{\dfrac{pq}{n}}\leq F_n\leq p+u_{\alpha}.\sqrt{\dfrac{pq}{n}}\right )\approx 1-\alpha $$
$$\text{ c'est-à-dire : } P\left (\left | F_n-p\right |\leq u_{\alpha}.\sqrt{\dfrac{pq}{n}}\right )\approx 1-\alpha $$
$$\text{ d'où } P\left (\left | F_n-p\right |\right )\leq \epsilon \approx 1-\alpha \text{ (niveau de confiance) dès que } u_{\alpha}.\sqrt{\dfrac{pq}{n}}\leq \epsilon $$ $$\text{ dès que } n\geq \dfrac{u_{\alpha}^2.p(1-p)}{\epsilon^2}$$
Algorithme : méthodes de Monte-Carlo
Le but de ces méthodes est de calculer des intégrales par des méthodes probabilistes.
Ces méthodes fonctionnent également pour des fonctions discontinues, ce qui explique son intérêt.
Pour simplifier, on calcule des intégrales de fonctions positives sur l'intervalle $[0;1]$ uniquement.
Méthode du rejet
On suppose qu'on connaît un majorant $M$ d'une fonction $f$ sur l'intervalle $[0;1]$.
Comme $\displaystyle\int_0^1 f(x)dx$ est l'aire du domaine $D=\left\{x\in[0;1], y\in[0;M],y\leq f(x)\right\}$, on tire aléatoirement un grand nombre de points dans le rectangle $[0;1]\times[0;M]$ (les coordonnées suivants des lois uniformes).
On fait ensuite le quotient entre les points situés dans $D$ et le nombre total de points. On obtient ainsi une approximation de $\displaystyle\int_0^1 f(x)dx$.
Programmer et tester cette méthode ($M$ et $n$ seront demandés à l'utilisateur)
Méthode de l'espérance
On simule $n$ (grand) valeurs $x_i, 1\leq i\leq n$ suivant une loi uniforme sur $[0;1]$. Alors $\displaystyle\dfrac{\displaystyle\sum_1^n f(x_i)}{n}$ est une bonne approximation de $\displaystyle\int_0^1 f(x)dx$
Programmer et tester cette méthode ($n$ sera demandé à l'utilisateur)
Algorithmique : Méthodes de calcul approché d'une intégrale
Exercice
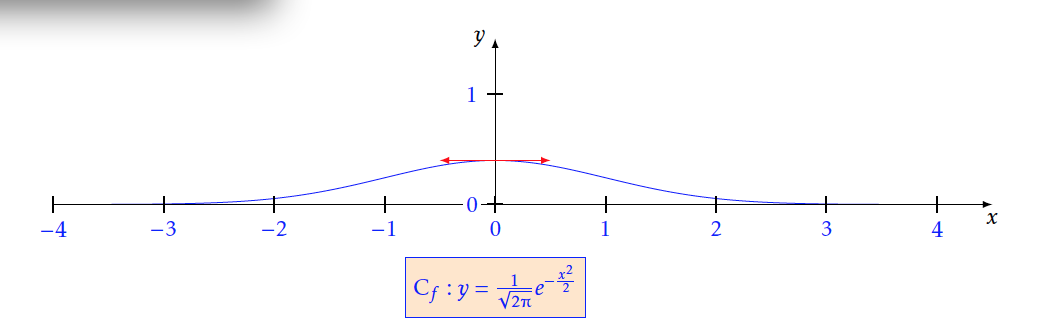
Soit $f$ la fonction définie sur $\mathbb{R}$par: $f(x) = \frac{1}{\sqrt {2\pi } }e^{ - \frac{{{x^2}}}{2}}$ On note $C_f$ le graphe représentatif de $f$ dans un rep ère $(O;I,J)$ du plan.
Partie A
- Démontrer que, pour tout $x$ de , $f(-x) = f(x)$. Que peut-on en déduire pour $C_f$ ?\\ $f(-x) = \frac{1}{{\sqrt {2\pi } }}{e^{ - \frac{{{(-x)^2}}}{2}}}= \frac{1}{{\sqrt {2\pi } }}{e^{ - \frac{{{x^2}}}{2}}}=f(x)$\\ On a pour tout $x \in \mathbb{R} ; f(-x)=f(x)$, ceci prouve que la fonction $f$ est paire , donc$C_f$ la représentation graphique de $f$ est symétrique par rapport à l'axe des ordonnées.
- Etudier le sens de variation de $f$ sur $\mathbb{R}{^ + }$.
$f$ est dérivable sur $\mathbb{R}$ et $f'(x)= \frac{1}{{\sqrt {2\pi } }}{(-x)e^{ - \frac{{{x^2}}}{2}}}=-xf(x)$
La fonction exponentielle étant strictement positive sur $\mathbb{R}$, $f'(x)$ a le signe de $-x$.
Donc pour tout $x>0$ on a $f'(x)<0$, ce qui prouve que la fonction $f$ est strictement décroissante sur $\mathbb{R} ^{+}$.
- Construire $C_f$ dans le repère précédent.
Figure
- Soit $ b$ un réel strictement positif. On cherche un encadrement de l'aire A du domaine compris entre $C_f$, l'axe $[0x)$ et les droites d'équation $x = 0$ et $x =b$.
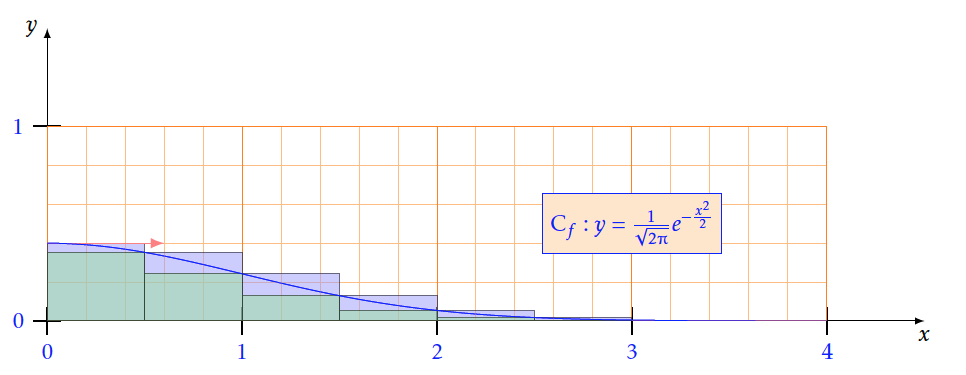
- A l'aide d'un logiciel de géométrie dynamique, effectuer une conjecture sur cette aire pour $b = 3$.
- Avec $n=6$
- Avec $n=12$
- Avec $n=40$
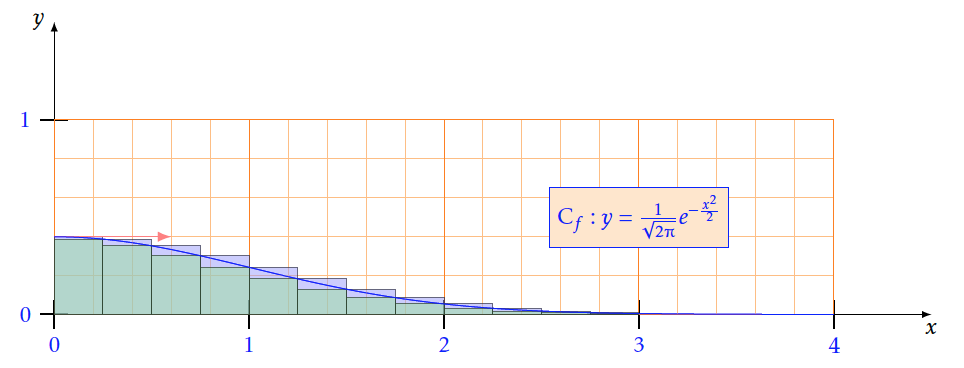
- Soit $f$ une fonction décroissante positive sur un intervalle $[a ; b]$ avec a$ < $b et n un entier$>$0. On définit $h=\frac{b-a}{n}$et on note I =$\displaystyle\int_a^bf\left(x\right)dx$ .Montrer que $h\sum\limits_{k = 1}^n {f(a + kh)} \le I \le h\sum\limits_{k = 0}^n {f(a + kh)} $
Posons $x_0=a$, $x_1=a+h$ et pour tout $k$ entier de $[0,n]$; $x_k=a+kh$ ;
on a $a=x_0< x_1 < \ldots< x_n=b$ $f$ est décroissante sur $[a,b]$, donc sur $[x_k;x_{k+1}]$;
Donc pour tout $x \in [x_k;x_{k+1}]$, on a $f\left (x_k\right )\geq f(x)\geq f\left (x_{k+1}\right )$
soit encore $f\left (x_{k+1}\right )\leq f(x)\leq f\left (x_{k}\right )$
On intègre sur l'intervalle $[x_k;x_{k+1}] $; on obtient $\displaystyle \int_{x_k}^{x_{k+1}} f\left (x_{k+1}\right )\,dx \leq \displaystyle \int_{x_k}^{x_{k+1}} f\left (x\right )\,dx\leq \displaystyle \int_{x_k}^{x_{k+1}} f\left (x_{k}\right )\,dx$
soit :$$h f\left (x_{k+1}\right ) \leq \displaystyle \int_{x_k}^{x_{k+1}} f\left (x\right )\,dx\leq h f\left (x_{k}\right )$$ Pour $k=0$ on a : $h f\left (x_{1}\right ) \leq \displaystyle \int_{x_0}^{x_{1}} f\left (x\right )\,dx\leq h f\left (x_{0}\right )$
Pour $k=1$ on a : $h f\left (x_{2}\right ) \leq \displaystyle \int_{x_1}^{x_{2}} f\left (x\right )\,dx\leq h f\left (x_{1}\right )$
Pour $k=2$ on a : $h f\left (x_{3}\right ) \leq \displaystyle \int_{x_2}^{x_{3}} f\left (x\right )\,dx\leq h f\left (x_{2}\right )$
$\cdots \cdots \cdots \cdots \cdots \cdots \cdots $
Pour $k=n-1$ on a : $h f\left (x_{n}\right ) \leq \displaystyle \int_{x_{n-1}}^{x_{n}} f\left (x\right )\,dx\leq h f\left (x_{n-1}\right )$
On ajoute membre à membres ces $n$ inégalités de même sens, et on utilise la relation de Chasles :
$$h\left [f\left (x_{1}\right )+f\left (x_{2}\right )+\cdots+f\left (x_{n}\right )\right ]\leq\displaystyle \int_{x_{0}}^{x_{n}} f\left (x\right )\,dx\leq h\left [f\left (x_{0}\right )+f\left (x_{1}\right )+\cdots+f\left (x_{n-1}\right )\right]$$ soit encore $h\sum\limits_{k = 1}^n {f(a + kh)} \le I \le h\sum\limits_{k = 0}^n {f(a + kh)} $
- En déduire un algorithme permettant d'encadrer I.
$$\begin{array} {|l |l|}\hline \text{Valeur approchée d'une intégrale } & \\ & \\ \text{ Variables : } & n, k \text{ deux entiers naturels, }\\ & Som_{inf}, Som_{sup} \text{ deux réels, }\\ \text{Entrées :}& \text{ Saisir } a.\\ & \text{ Saisir } b.\\ & a \text{ et } b \text{ nombres réels, les bornes de l'intégrale} \\ & \text{ Saisir } n.\\ & n \text{ entier ,le nombre de rectangles utilisé pour faire l'approximation} \\ & \text{ Saisir } f.\\ & f \text{ fonction ,la fonction à intégrer sur [a;b]} \\ \text{Initialisation :}& \\ & Som_{inf} \text{ prend la valeur } 0.\\ & Som_{sup} \text{ prend la valeur } 0.\\ \text{ Traitement : } & \\ & h \text{ prend la valeur } \dfrac{b-a}{n}\\ & \text{ Pour } k \text{ variant de 1 à } n\\ & \quad \text{ Faire } \\ & \quad Som_{inf} \text{ prend la valeur } Som_{inf}+h\times f(a+kh).\\ & \quad Som_{sup} \text{ prend la valeur } Som_{sup}+h\times f(a+(k-1)h).\\& \text{ Fin Pour } \\ \text{ Sortie : } & \text{ Afficher } Som_{inf}\\ & \text{ Afficher } Som_{sup} \\ \hline \end{array}$$
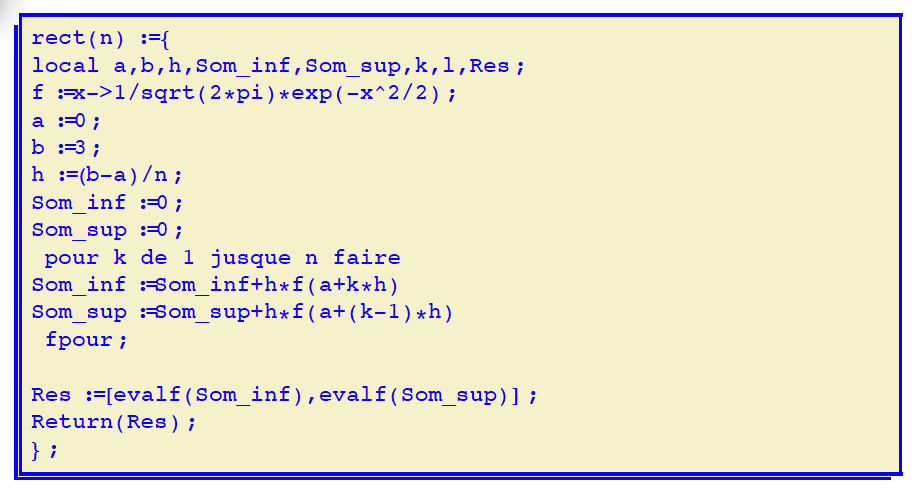
- Transcrire cet algorithme en langage machine pour la fonction $f$ définie dans l'énoncé :
Son utilisation :
rect(100);
renvoie :
[0.492731448412,0.504566761372]
seq(rect(100*k),k=1..5);
[0.492731448412,0.504566761372],[0.495691024443,0.501608680922],[0.496677439013,0.500622543333],[0.497170625526,0.500129453766],[0.497466530786,0.499833593378]
- Quelle conjecture peut-on formuler sur l'aire du domaine compris entre $C_f$ et l'axe [Ox) ?
Cette aire vaut 1 unité d'aire ...( cf cours de probabilité)
Partie B
Dans la suite de l'exercice, on utilisera l'algorithme suivant, algorithme permettant de calculer la valeur approchée d'une intégrale sous la forme d'une fonction:
$$\begin{array} {|l |l|}\hline \text{Fonction Valeur approchée d'une intégrale } & \\ \text{Une approximation de l'intégrale par la méthode Simpson } & \\ & \\ \text{ Variables : } & n \text{ un entier naturel, }\\ & a, b \text{ deux réels, }\\ \text{Entrées :}& \\ & f \text{ fonction ,la fonction à intégrer sur [a;b]} \\ \text{Initialisation :}& \\ & S \text{ prend la valeur } 0.\\ & m \text{ prend la valeur } a.\\ \text{ Traitement : } & \\ & h \text{ prend la valeur } \dfrac{b-a}{n}\\ & \text{ Tant que } m < b\\ & \quad \text{ Faire } \\ & \quad S \text{ prend la valeur } S+S+(f(m)+4*f(m+h/2)+f(m+h))*(h/6).\\ & \quad m \text{ prend la valeur } m+h.\\ \text{ Sortie : } & \text{ Afficher } S.\\ \hline \end{array}$$
Transcrire cet algorithme en langage machine pour la fonction f définie dans l'énoncé
Avec XCAS : rect(n):={ local a,b,h,Som_inf,Som_sup,k,l,Res;
f:=x->1/sqrt(2*pi)*exp(-x^2/2);
a:=0; b:=3; h:=(b-a)/n;
Som_inf:=0; Som_sup:=0;
pour k de 1 jusque n
faire
Som_inf:=Som_inf+h*f(a+k*h)
Som_sup:=Som_sup+h*f(a+(k-1)*h)
fpour;
Res:=[evalf(Som_inf),evalf(Som_sup)]; Return(Res); };
Son utilisation : rect(100);
renvoie :
[0.492731448412,0.504566761372]
seq(rect(100*k),k=1..5);
renvoie :
[0.492731448412,0.504566761372],[0.495691024443,0.501608680922],[0.496677439013,0.500622543333],[0.497170625526,0.500129453766],[0.497466530786,0.499833593378]
Exercice
- On considère la fonction $F$ définie sur $\mathbb{R}^+$ par : $F\left(t\right)=\displaystyle\int_0^t\dfrac{1}{\sqrt{2\pi{}}}e^{-\dfrac{x^2}{2}}dx$ Montrer que, pour tout réel $\alpha{}$ de ]0 ; 1], ,il existe un seul réel positif $b$ tel que $F\left(b\right)=0,5-\frac{\alpha{}}{2}$;
$b$ est noté $u_{\alpha{}}$ .
Déjà comme $\alpha \in ]0;1]$; on a $0,5-\frac{\alpha{}}{2} \in \left [0;\dfrac{1}{2}\right[$.
Il s'agit donc ici de déterminer un antécédent $b$ du nombre $0,5-\frac{\alpha{}}{2}$, on utilise ici le théorème de la bijection !
La fonction $f:x\mapsto \frac{1}{\sqrt{2\pi{}}}e^{-\frac{x^2}{2}}$ est continue sur $\mathbb{R}$, donc la fonction $F$ définie sur $\mathbb{R}^+$ par $F\left(t\right)=\int_0^t\frac{1}{\sqrt{2\pi{}}}e^{-\frac{x^2}{2}}dx$ est la primitive de $f$ qui s'annule en 0.
Ainsi $F$ est dérivable sur $\mathbb{R}^+$ et $F'(x)=f(x)$,
la fonction exponentielle étant strictement positive sur $\mathbb{R}$, on a donc :
$\forall x \in \mathbb{R}; F'(x)>0$
Par ailleurs $\lim\limits_{x\rightarrow +\infty}F(x)=\dfrac{1}{2}$
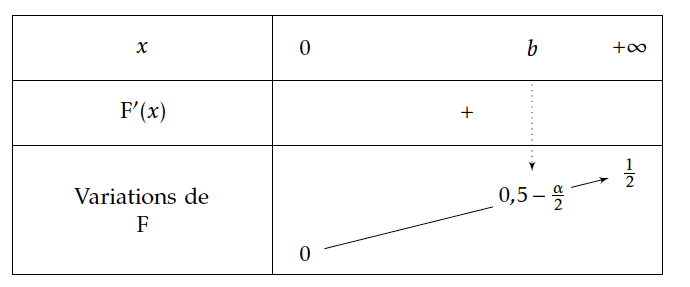
$F$ est donc continue car dérivable , strictement croissante sur $[0;+\infty[$,
donc $F$ réalise une bijection de $[0;+\infty[$ sur $\left[F(0);\lim\limits_{x\rightarrow +\infty}F(x)\right[$ soit sur $\left[0;\dfrac{1}{2}\right[$.
Or $0,5-\frac{\alpha{}}{2} \in \left [0;\dfrac{1}{2}\right[$,
donc l'équation $F(x)=0,5-\frac{\alpha{}}{2}$ a une solution unique $b$ dans $[0;+\infty[$.
- En utilisant l'algorithme donné précédemment, construire un algorithme permettant, pour un nombre $\alpha{}$donné de ]0 ; 1], de déterminer une valeur approchée de ${u_\alpha }$.
$$\begin{array} {|l |l|}\hline \text{Approximation de } u_{\alpha} & \\ \text{Une approximation ... } & \\ & \\ \text{Entrées :}& \\ & \text{ Saisir } \alpha \text{ un réel de ]0;1] } \\ & \text{ Saisir } h \text{ le pas dans la méthode d'intégration } \\ & \text{ Saisir } f \text{ la fonction à intégrer sur [a;b] } \\ \text{Initialisation :}& \\ & b \text{ prend la valeur } 0.\\ & h \text{ prend la valeur } 0.01\\ \text{ Traitement : } & \\ & h \text{ prend la valeur } \dfrac{b-a}{n}\\ & \text{ Tant que } Simpson(0,b,0.01) < 0.5-alpha/2 \\ & \quad \text{ Faire } \\ & \quad S \text{ prend la valeur } S+S+(f(m)+4*f(m+h/2)+f(m+h))*(h/6).\\ & \quad b \text{ prend la valeur } b+h.\\ \text{ Sortie : } & \text{ Afficher } b.\\ \hline \end{array}$$