Baccalauréat STL biotechnologies Polynésie 11 juin 2015 - Exercice 2

Page 3 sur 8: Exercice 2

Exercice 2 6 points

Suites

On injecte dans le sang d’un malade un médicament à l’aide d’une perfusion. L’efficacité de ce médicament est optimale lorsque le débit de la perfusion est stable et que la concentration du produit ne dépasse pas 250 microgrammes (\micro g) par cm$^3$, seuil au-delà duquel des effets indésirables et toxiques apparaissent. On relève l’évolution de la concentration de ce médicament et on obtient les résultats suivants :
$$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline \text{Temps }t_i \text{ en minutes } &0 & 2& 4 &6 & 10 &12 & 15\\\hline \text{ Concentration } c_i \text{ en } \mu g \text{ par }cm ^3 &0 &64&94 &130 & 195&220 & 230\\\hline \end{array} $$
Dans cet exercice, les résultats seront arrondis à $10^{-2}$.

Partie A

On pose : $y_i = \ln \left(250 - c_i\right)$ où $\ln$ désigne la fonction logarithme népérien.

1. Recopier et compléter le tableau suivant (donner des valeurs arrondies à $10^{-2}$ ) :
   $$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline \text{ Temps } t_i \text{ en minutes } &0 & 2 & 4 & 6 & 10&12 & 15\\\hline y_i = \ln \left(250 - c_i\right) & & & & & & &\\\hline \end{array} $$
2. Dans un repère orthogonal d’unités $1 cm $ en abscisse et $2 cm$ en ordonnée, représenter le nuage de points $M_i\ \left(t_i~;~ y_i\right)$ de la série statistique définie par le tableau précédent.
3. Déterminer une équation de la droite $\mathcal{D}$ d’ajustement affine de $y$ en $t$ obtenue par la méthode des moindres carrés. Représenter cette droite dans le repère précédent.
4. En déduire une relation entre la concentration $c$ et le temps $t$ sous la forme $c = A + B \text{e}^{k t}$.

 

Partie B

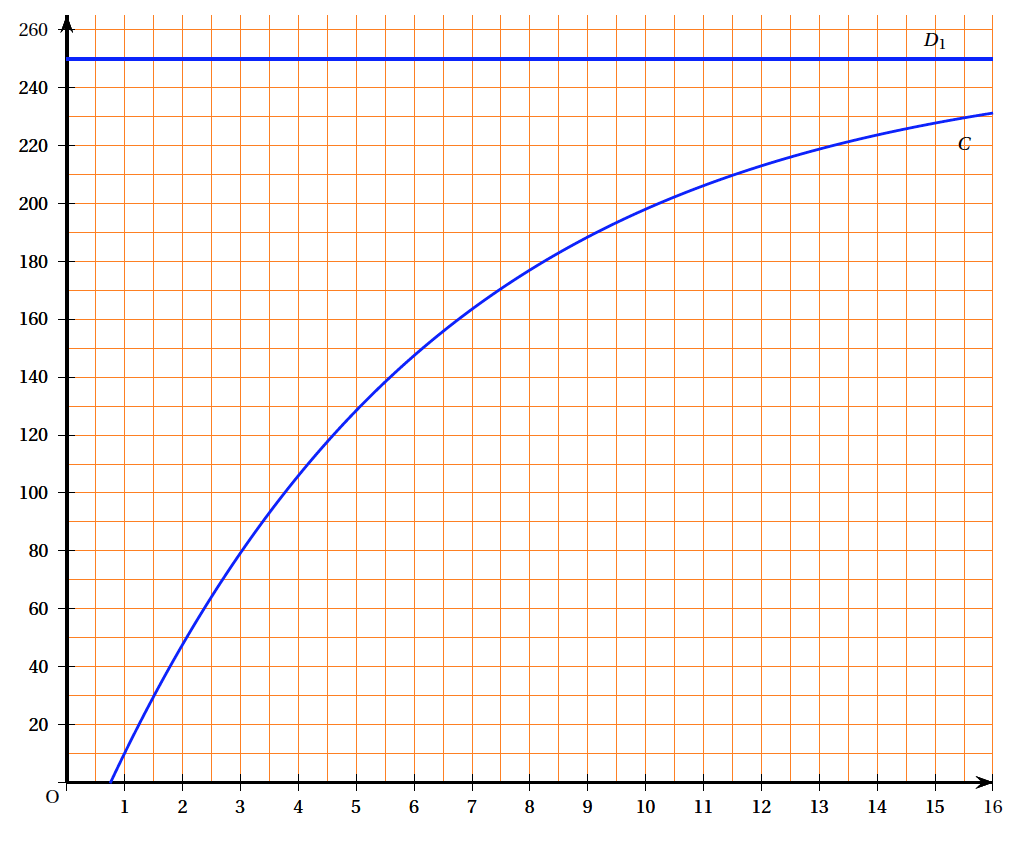
Soit la fonction $f$ définie sur $[0~;~+\infty[$ par $f(t)=250 - 284,29\text{e}^{- 0,17t}$. On admet que la fonction $f$ donne une bonne approximation de la concentration du médicament. La courbe $\mathcal{C}$ de la fonction $f$ et son asymptote $D_1$ d’équation $y = 250$ sont données en annexe 1.

1. En justifiant, déterminer graphiquement le signe de la fonction dérivée de $f$ sur $[0~;~+\infty[$.
2. En justifiant, déterminer graphiquement la limite de $f$ en $+\infty$.
3. Justifier que la concentration du médicament ne dépasse pas $ 250\mu g$ par cm$^3$.
4. 1. Résoudre sur $[0,+\infty[$ l’inéquation $f (t) > 180$ .
   2. En déduire, à une minute près, le temps nécessaire pour atteindre la dose efficace qui est de $ 180\mu g$ par cm$^3$.
5. Retrouver ce résultat en utilisant le graphique de la partie A (on expliquera la démarche utilisée en laissant les traits de construction apparents).

ANNEXE 1(À RENDRE AVEC LA COPIE)

EXERCICE 2