Baccalauréat S Liban 31 mai 2019 - Correction Exercice 1
Page 2 sur 10
Correction de l'exercice 1 (5 points)
Le plan est muni d'un repère orthogonal (O, I, J).
- On considère la fonction $f$ définie sur l'intervalle $]0 ; 1]$ par \[f(x) = x(1 - \ln x)^2.\]
- Déterminer une expression de la fonction dérivée de $f$ et vérifier que pour tout $x \in ]0~;~1]$, $f'(x) = (\ln x + 1)(\ln x - 1)$. La fonction $f$ est dérivable sur $\mathbb R$ en tant que somme et produit de fonctions dérivables.
- Étudier les variations de la fonction $f$ et dresser son tableau de variations sur l'intervalle ]0~;~1] (on admettra que la limite de la fonction $f$ en 0 est nulle). Pour tout réel $x\in ]0;1]$ on a $\ln x\leq 0$ donc $\ln x-1\leq 0$.
Pour tout réel $x\in ]0;1]$ on a :
$\begin{align*} f'(x)&=\left(1-\ln x\right)^2+x\times \dfrac{-2}{x}\times \left(1-\ln x\right) \\
&=\left(1-\ln x\right)\left(\left(1-\ln x\right)-2\right)\\
&=\left(1-\ln x\right)\left(-1-\ln x\right) \\
&=-\left(1-\ln x\right)\left(1+\ln x\right)\\
&=\left(\ln x-1\right)\left(1+\ln x\right)\end{align*}$
$\quad$
$1+\ln x=0 \iff \ln x=-1 \iff x=\text{e}^{-1}$
et $1+\ln x>0 \iff \ln x>-1 \iff x>\text{e}^{-1}$.
Dressonss alors le tableau d signe de la dérivée :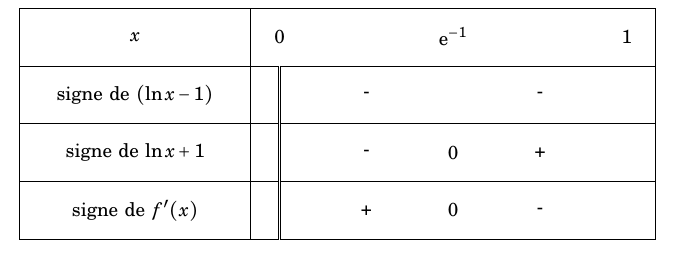
On obtient donc le tableau de variations suivant :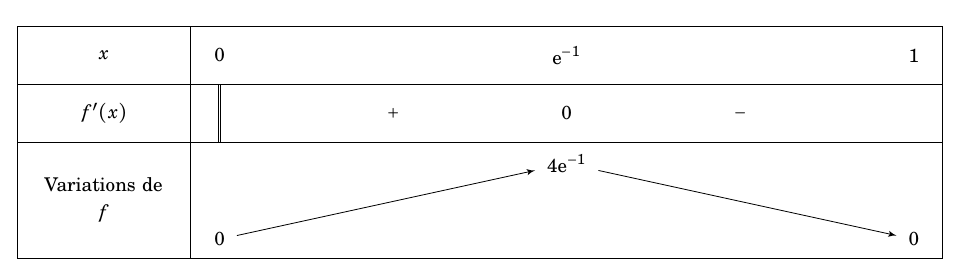
On note $\Gamma$ la courbe représentative de la fonction $g$ définie sur l'intervalle $]0~;~1]$ par $g(x) = \ln x$. Soit $a$ un réel de l'intervalle $ ]0~;~1]$. On note $M_a$ le point de la courbe $\Gamma$ d'abscisse $a$ et $d_a$ la tangente à la courbe $\Gamma$ au point $M_a$. Cette droite $d_a$ coupe l'axe des abscisses au point $N_a$ et l'axe des ordonnées au point $P_a$ . On s'intéresse à l'aire du triangle O$N_aP_a$ quand le réel $a$ varie dans l'intervalle $]0~;~1]$.
- Dans cette question, on étudie le cas particulier où $a = 0,2$ et on donne la figure ci-dessous.
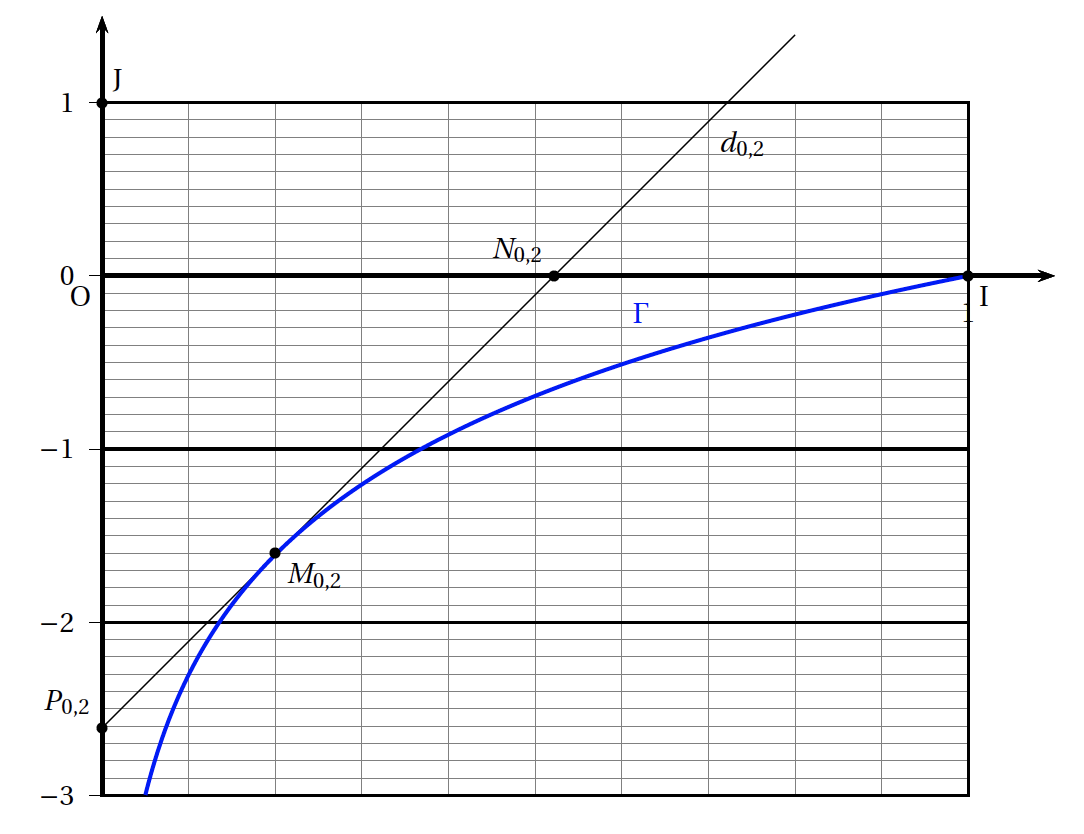
- Déterminer graphiquement une estimation de l'aire du triangle O$N_{0,2}P_{0,2}$ en unités d'aire. Graphiquement l’aire du triangle $ON_{0,2}P_{0,2}$ est $\mathscr{A}(0,2)=\dfrac{0,52\times 2,6}{2}=0,676$ u.a.
- Déterminer une équation de la tangente $d_{0,2}$. Par définition de la fonction $\ln$ la fonction $g$ est dérivable sur l’intervalle $]0;1]$.
- Calculer la valeur exacte de l'aire du triangle O$N_{0,2}P_{0,2}$ . Dans ce qui suit, on admet que, pour tout réel $a$ de l'intervalle ]0 ; 1], l'aire du triangle O$N_aP_a$ en unités d'aire est donnée par $\mathcal{A}(a) = \dfrac{1}{2}a (1 - \ln a)^2$. Ainsi le point$P_{0,2}$ a pour coordonnées $\left(0;\ln(0,2)-1\right)$.
$\quad$
Une équation de la tangente $d_{0,2}$ est de la forme :
$y=g'(0,2)(x-0,2)+g(0,2)$
Or $g'(x)=\dfrac{1}{x}$ donc $g'(0,2)=5$.
Une équation de cette tangente est donc :
$y=5(x-0,2)+\ln(0,2)$ soit $y=5x+\ln(0,2)-1$.
$\quad$
et $5x+\ln(0,2)-1=0\iff x=\dfrac{1-\ln(0,2)}{5}$
Le point $N_{0,2}$ a pour coordonnées $\left(\dfrac{1-\ln(0,2)}{5};0\right)$.
L’aire du triangle $ON_{0,2}P_{0,2}$ est donc :
$\begin{align*} \mathscr{A}(0,2)&=\dfrac{\left|\dfrac{1-\ln(0,2)}{5}\times \left(\ln(0,2)-1\right)\right|}{2}\\
&=\dfrac{\left(1-\ln(0,2)\right)^2}{10}\end{align*}$
$\quad$ - À l'aide des questions précédentes, déterminer pour quelle valeur de $a$ l'aire $\mathcal{A}(a)$ est maximale. Déterminer cette aire maximale. On a ainsi $\mathscr{A}(a)=\dfrac{f(a)}{2}$.
D’après le tableau de variation de la fonction $f$, l’aire est donc maximale pour $a=\text{e}^{-1}$ et elle vaut alors $2\text{e}^{-1}$.
$\quad$
- Vues: 81413
