Baccalauréat S Liban 31 mai 2019
Page 1 sur 10
Exercice 1 5 points
Le plan est muni d'un repère orthogonal (O, I, J).
- On considère la fonction $f$ définie sur l'intervalle ]0 ; 1] par \[f(x) = x(1 - \ln x)^2.\]
- Déterminer une expression de la fonction dérivée de $f$ et vérifier que pour tout $x \in ]0~;~1]$, $f'(x) = (\ln x + 1)(\ln x - 1)$.
- Étudier les variations de la fonction $f$ et dresser son tableau de variations sur l'intervalle $]0~;~1]$ (on admettra que la limite de la fonction $f$ en 0 est nulle).
On note $\Gamma$ la courbe représentative de la fonction $g$ définie sur l'intervalle $]0~;~1]$ par $g(x) = \ln x$. Soit $a$ un réel de l'intervalle $ ]0~;~1]$. On note $M_a$ le point de la courbe $\Gamma$ d'abscisse $a$ et $d_a$ la tangente à la courbe $\Gamma$ au point $M_a$. Cette droite $d_a$ coupe l'axe des abscisses au point $N_a$ et l'axe des ordonnées au point $P_a$ . On s'intéresse à l'aire du triangle O$N_aP_a$ quand le réel $a$ varie dans l'intervalle $]0~;~1]$.
- Dans cette question, on étudie le cas particulier où $a = 0,2$ et on donne la figure ci-dessous.
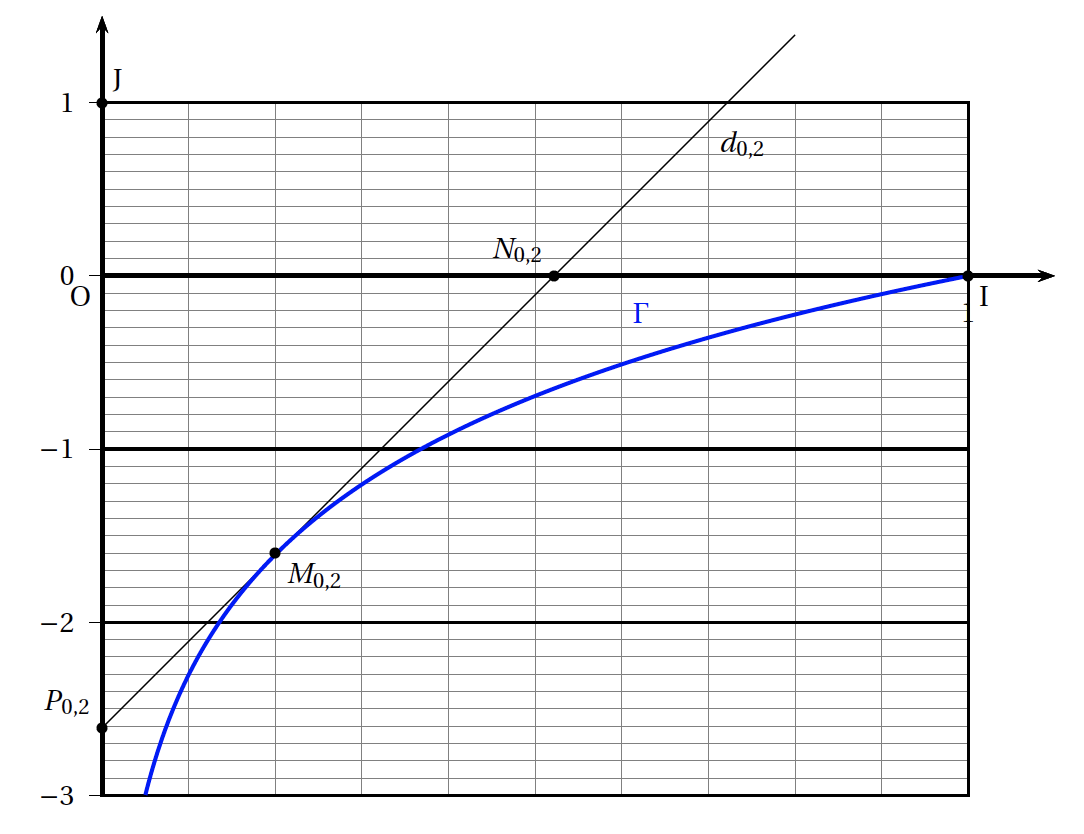
- Déterminer graphiquement une estimation de l'aire du triangle O$N_{0,2}P_{0,2}$ en unités d'aire.
- Déterminer une équation de la tangente $d_{0,2}$.
- Calculer la valeur exacte de l'aire du triangle O$N_{0,2}P_{0,2}$ . Dans ce qui suit, on admet que, pour tout réel $a$ de l'intervalle ]0 ; 1], l'aire du triangle O$N_aP_a$ en unités d'aire est donnée par $\mathcal{A}(a) = \dfrac{1}{2}a (1 - \ln a)^2$.
- À l'aide des questions précédentes, déterminer pour quelle valeur de $a$ l'aire $\mathcal{A}(a)$ est maximale. Déterminer cette aire maximale.
- Vues: 86555
