Baccalauréat S Amérique du Sud 22 novembre 2016
Exercice 1 5 points
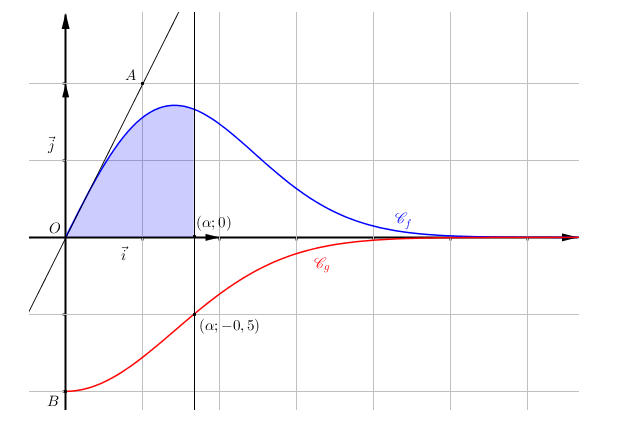
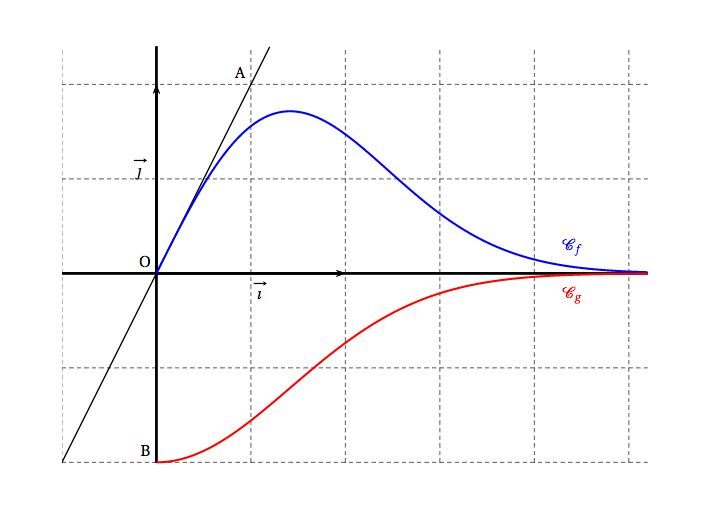
Les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ données en annexe 1 sont les représentations graphiques, dans un repère orthonormé $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$, de deux fonctions $f$ et $g$ définies sur $[0~;~+ \infty[$. On considère les points A(0,5 ; 1) et B$(0 ; -1)$ dans le repère $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$. On sait que O appartient à $\mathcal{C}_f$ et que la droite (OA) est tangente à $\mathcal{C}_f$ au point O.
- On suppose que la fonction $f$ s'écrit sous la forme $f(x) = (ax + b)\text{e}^{- x^2}$ où $a$ et $b$ sont des réels. Déterminer les valeurs exactes des réels $a$ et $b$, en détaillant la démarche.
-
- On admettra que, pour tout réel $x$ strictement positif, $f(x) = \dfrac{2}{x}\times \dfrac{x^2}{\text{e}^{x^2}}$. Calculer $\displaystyle\lim_{x \to + \infty} f(x)$.
- Dresser, en le justifiant, le tableau de variations de la fonction $f$ sur $[0~;~+ \infty[$.
- La fonction $g$ dont la courbe représentative $\mathcal{C}_g$ passe par le point B$(0~;~-1)$ est une primitive de la fonction $f$ sur $[0~;~+ \infty[$.
- Déterminer l'expression de $g(x)$.
- Soit $m$ un réel strictement positif. Calculer $I_m = \displaystyle\int_0^{m} f(t)\:\text{d}t$ en fonction de $m$.
- Déterminer $\displaystyle\lim_{m \to + \infty} I_m$.
-
- Justifier que $f$ est une fonction densité de probabilité sur $[0~;~+ \infty[$.
- Soit $X$ une variable aléatoire continue qui admet la fonction $f$ comme densité de probabilité. Justifier que, pour tout réel $x$ de $[0~;~+ \infty[$, $P(X \leqslant x) = g(x) + 1$.
- En déduire la valeur exacte du réel $\alpha$ tel que $P(X \leqslant \alpha) = 0,5$.
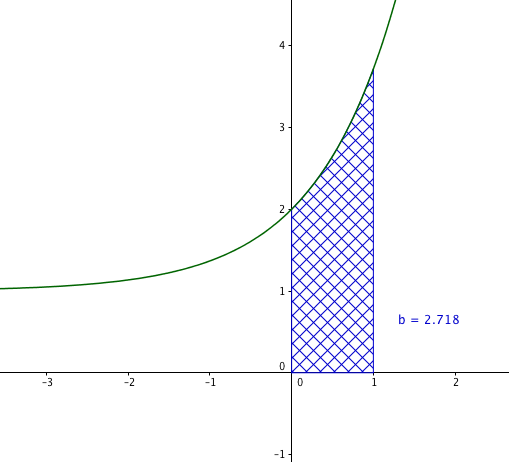
- Sans utiliser une valeur approchée de $\alpha$, construire dans le repère de l'annexe 1 le point de coordonnées $(\alpha~;~0)$ en laissant apparents les traits de construction. Hachurer ensuite la région du plan correspondant à $P(X \leqslant \alpha)$.
Désormais, on considère que $f(x) = 2x\text{e}^{- x^2}$ pour tout $x$ appartenant à $[0~;~+ \infty[$
Annexe de l'exercice 1
Correction de l'exercice 1 (5 points)
Les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ données en annexe 1 sont les représentations graphiques, dans un repère orthonormé $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$, de deux fonctions $f$ et $g$ définies sur $[0~;~+ \infty[$. On considère les points A(0,5 ; 1) et B$(0 ; -1)$ dans le repère $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$. On sait que O appartient à $\mathcal{C}_f$ et que la droite (OA) est tangente à $\mathcal{C}_f$ au point O.
- On suppose que la fonction $f$ s'écrit sous la forme $f(x) = (ax + b)\text{e}^{- x^2}$ où $a$ et $b$ sont des réels. Déterminer les valeurs exactes des réels $a$ et $b$, en détaillant la démarche. On peut lire que $f(0)=0$ et que $f'(0)=2$ (coefficient directeur de la tangente $(OA)$).
-
- On admettra que, pour tout réel $x$ strictement positif, $f(x) = \dfrac{2}{x}\times \dfrac{x^2}{\text{e}^{x^2}}$. Calculer $\displaystyle\lim_{x \to + \infty} f(x)$. $\lim\limits_{x \to +\infty} x^2=+\infty$ et $\lim\limits_{X \to +\infty} \dfrac{e^X}{X}=+\infty$.
- Dresser, en le justifiant, le tableau de variations de la fonction $f$ sur $[0~;~+ \infty[$. Pour tout réel $x\geq 0$, $f'(x)=2\text{e}^{-x^2}-4x^2\text{e}^{-x^2}=2(1-2x^2)\text{e}^{-x^2}$
Donc $\lim\limits_{x \to +\infty} \dfrac{\text{e}^{x^2}}{x^2}=+\infty$ et $\lim\limits_{x \to +\infty} \dfrac{x^2}{\text{e}^{x^2}}=0$
De plus $\lim\limits_{x \to +\infty} \dfrac{2}{x}=0$
Par produit on a donc $\lim\limits_{x \to +\infty} f(x)=0$.
$\quad$
La fonction exponentielle est strictement positive sur $\mathbb R$ donc le signe de $f'(x)$ ne dépend que de celui de $1-2x^2$.
Or $1-2x^2=\left(1-\sqrt{2}x\right)\times \left(1+\sqrt{x}\right)$.
Sur $[0;+\infty[$ on a $\left(1+\sqrt{x}\right) >0$.
$1-\sqrt{2}x=0 \iff x=\dfrac{1}{\sqrt{2}} \iff x=\dfrac{\sqrt{2}}{2}$
On en déduit donc le tableau de variation suivant :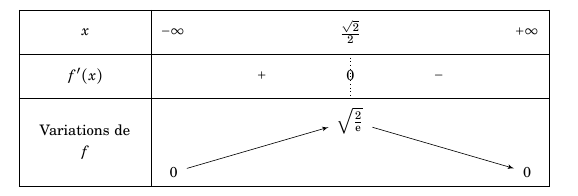 $f \left(\frac{\sqrt{2}}{2} \right)=2\times \frac{\sqrt{2}}{2} \text{e}^{-\frac{1}{2}}= \sqrt 2 \times \frac{1}{\text{e}^{\frac{1}{2}}}= \sqrt{\frac{2}{\text{e}}} $
$f \left(\frac{\sqrt{2}}{2} \right)=2\times \frac{\sqrt{2}}{2} \text{e}^{-\frac{1}{2}}= \sqrt 2 \times \frac{1}{\text{e}^{\frac{1}{2}}}= \sqrt{\frac{2}{\text{e}}} $ - La fonction $g$ dont la courbe représentative $\mathcal{C}_g$ passe par le point B$(0~;~-1)$ est une primitive de la fonction $f$ sur $[0~;~+ \infty[$.
- Déterminer l'expression de $g(x)$. $f$ est de la forme $-u’\text{e}^{u}$.
- Soit $m$ un réel strictement positif. Calculer $I_m = \displaystyle\int_0^{m} f(t)\:\text{d}t$ en fonction de $m$. $\begin{align*} I_m&=\int_0^m f(t)\text{d}t \\ &=g(m)-g(0) \\ &=-\text{e}^{-m^2}+1
- Déterminer $\displaystyle\lim_{m \to + \infty} I_m$. $\lim\limits_{m \to +\infty} -m^2=-\infty$ et $\lim\limits_{X \to -\infty} \text{e}^X=0$ donc $\lim\limits_{m \to +\infty} e^{-x^2}=0$ et $\lim\limits_{m \to +\infty} I_m=1$
Donc une primitive de la fonction $f$ sur $[0;+\infty[$ est de la forme $g(x)=-\text{e}^{-x^2}+c$.
On sait que $g(0)=-1$ puisque la courbe $\mathscr{C}_g$ passe par le point $B(0;-1)$.
Or $g(0)=-1+c$.
Par conséquent $-1+c=-1$ et $c=0$.
On en déduit donc que, sur $[0;+\infty[$, une primitive de la fonction $f$ est la fonction $g$ définie par $g(x)=-\text{e}^{-x^2}$ dont la courbe représentative passe par le point $B$.
$\quad$
\end{align*}$
$\quad$
$\quad$ -
- Justifier que $f$ est une fonction densité de probabilité sur $[0~;~+ \infty[$. Pour tout réel $x$ positif on a : $2x \geq 0$ et $\text{e}^{-x^2} \geq 0$ (car la fonction exponentielle est strictement positive).
- Soit $X$ une variable aléatoire continue qui admet la fonction $f$ comme densité de probabilité. Justifier que, pour tout réel $x$ de $[0~;~+ \infty[$, $P(X \leqslant x) = g(x) + 1$. Pour tout réel $x$ positif, on a :
- En déduire la valeur exacte du réel $\alpha$ tel que $P(X \leqslant \alpha) = 0,5$. $\begin{align*} P(X \leq \alpha) = 0,5 &\iff g(\alpha)+1=0,5 \\ &\iff g(\alpha)=-0,5 \\ &\iff -\text{e}^{-\alpha^2}=-0,5 \\ &\iff \text{e}^{-\alpha^2}=0,5 \\ &\iff -\alpha^2 = \ln 0,5 \\ &\iff v^2=-\ln 0,5 \\ &\iff \alpha^2=- \left(-\ln 2\right) \\ &\iff \alpha^2=\ln 2 \\ &\iff \alpha=\sqrt{\ln 2} \text{ ou } \alpha=-\sqrt{\ln 2} \\ &\iff \alpha=\sqrt{\ln 2} \text{ car } \alpha \geq 0
- Sans utiliser une valeur approchée de $\alpha$, construire dans le repère de l'annexe 1 le point de coordonnées $(\alpha~;~0)$ en laissant apparents les traits de construction. Hachurer ensuite la région du plan correspondant à $P(X \leqslant \alpha)$.
Par conséquent $f(x) \geq 0$. (on pouvait également utiliser le tableau de variation)
$f$ est continue sur $[0;+\infty[$ en tant que produit de fonctions continues sur cet intervalle.
De plus, d’après la question précédente, $\lim\limits_{m \to +\infty} \displaystyle \int_0^m f(t)\text{d}t = 0$.
La fonction $f$ est donc une fonction densité de probabilité sur $[0;+\infty[$.
$\quad$
$P(X \leq x) = \displaystyle \int_0^x f(t)\text{d}t=g(x)-g(0)=g(x)+1$
$\quad$
\end{align*}$
$\quad$
Or $f(0)=b$ donc $b=0$
La fonction $f$ est dérivable sur $[0;+\infty[$ en tant que produit et composition de fonctions dérivables sur cet intervalle.
On a $f(x)=ax\text{e}^{-x^2}$ car on vient de montrer que $b=0$.
$f'(x)=a\text{e}^{-x^2}-2ax^2\text{e}^{-x^2}$
Donc $f'(0)=a$. Par conséquent $a=2$.
$\quad$
Désormais, on considère que $f(x) = 2x\text{e}^{- x^2}$ pour tout $x$ appartenant à $[0~;~+ \infty[$
Exercice 2 3 points
Pour chacune des trois propositions suivantes, indiquer si elle est vraie ou fausse et justifier la réponse choisie. Il est attribué un point par réponse exacte correctement justifiée. Une réponse non justifiée n'est pas prise en compte.
On munit le plan complexe d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$.
Proposition 1
L'ensemble des points du plan d'affixe $z$ tels que $|z - 4| = |z + 2\text{i}|$ est une droite qui passe par le point A d'affixe 3i.
Proposition 2
Soit $(E)$ l'équation $(z -1)\left(z^2 - 8z + 25\right) = 0$ où $z$ appartient à l'ensemble $\mathbb C$ des nombres complexes. Les points du plan dont les affixes sont les solutions dans $\mathbb C$ de l'équation $(E)$ sont les sommets d'un triangle rectangle.
Proposition 3
$\dfrac{\pi}{3}$ est un argument du nombre complexe $\left(- \sqrt{3} + \text{i}\right)^8$.
Correction de l'exercice 2 (3 points)
Pour chacune des trois propositions suivantes, indiquer si elle est vraie ou fausse et justifier la réponse choisie. Il est attribué un point par réponse exacte correctement justifiée. Une réponse non justifiée n'est pas prise en compte.
On munit le plan complexe d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$.
Proposition 1
L'ensemble des points du plan d'affixe $z$ tels que $|z - 4| = |z + 2\text{i}|$ est une droite qui passe par le point A d'affixe 3i.
On appelle $B$ le point d’affixe $4$, $C$ celui d’affixe $-2\text{i}$ et $M$ celui d’affixe $z$.
Par conséquent $|z-4|=|z+2\text{i}| \iff BM=CM$.
L’ensemble cherché est donc la médiatrice du segment $[BC]$.
Calculons $AB=|4-3\text{i}|=\sqrt{4^2+(-3)^2}=5$
et $AC=|-2\text{i}-3\text{i}|=|-5\text{i}|=5$.
Ainsi $AB=AC$. Le point $A$ appartient à la médiatrice du segment $[BC]$.
La proposition est vraie.
$\quad$
Proposition 2
Soit $(E)$ l'équation $(z -1)\left(z^2 - 8z + 25\right) = 0$ où $z$ appartient à l'ensemble $\mathbb C$ des nombres complexes. Les points du plan dont les affixes sont les solutions dans $\mathbb C$ de l'équation $(E)$ sont les sommets d'un triangle rectangle.
Résolvons tout d’abord l’équation $z^2-8z+25=0$
$\Delta = (-8)^2-4\times 25 = -36<0$
Cette équation possède donc deux racines complexes conjuguées :
$z_1=\dfrac{8-\text{i}\sqrt{36}}{2}=4-3\text{i}$ et $z_2=4+3\text{i}$
$(z-1)(z^2-8z+25)=0 \iff z-1=0 \text{ ou } z^2-8z+25=0$
Les solutions de l’équation $(E)$ sont donc $\lbrace 1;4-3\text{i};4+3\text{i} \rbrace$
On appelle $A$ le point d’affixe $1$, $B$ celui d’affixe $4-3\text{i}$ et $C$ celui d’affixe $4+3\text{i}$.
$AB=\left|4-3\text{i}-1\right| = \left|3-3\text{i}\right|=\sqrt{18}$
$AC=\left|4+3\text{i}-1\right| = \left|3+3\text{i}\right|=\sqrt{18}$
$BC=\left|4+3\text{i}-4+3\text{i}\right|=\left|6\text{i}\right|=6$
Dans le triangle $ABC$, le plus grand côté est $[BC]$.
D’une part $BC^2=36$.
D’autre part $AB^2+AC^2=18+18=36$.
D’après la réciproque du théorème de Pythagore, le triangle $ABC$ est rectangle en $A$.
La proposition est vraie.
Remarque : on pouvait également déterminer l’argument du nombre complexe $\dfrac{z_1-1}{z_2-1}$ et montrer que celui-ci était égal à $\pm \dfrac{\pi}{2}$.
$\quad$
Proposition 3
$\dfrac{\pi}{3}$ est un argument du nombre complexe $\left(- \sqrt{3} + \text{i}\right)^8$.
On a $\left|-\sqrt{3}+\text{i}\right|=2$ donc $\sqrt{3}+\text{i}=2\left|-\dfrac{\sqrt{3}}{2}+\dfrac{\text{i}}{2}\right|=2\text{e}^{5\text{i}\pi/6}$.
Par conséquent un argument de $\left(-\sqrt{3}+\text{i}\right)$ est $8\times \dfrac{5\pi}{6}=\dfrac{20\pi}{3}=6\pi+\dfrac{2\pi}{3}$.
Par conséquent, la mesure principale de cet argument est $\dfrac{2\pi}{3}$ et non $\dfrac{\pi}{3}$.
La proposition est fausse.
Exercice 3 3 points
La suite $\left(u_n\right)$ est définie par : \[ u_0 = 0 \quad \text{et, pour tout entier naturel }\:n, \:u_{n+1} = \dfrac{1}{2 - u_n}.\]
-
- À l'aide du calcul des premiers termes de la suite $\left(u_n\right)$, conjecturer la forme explicite de $u_n$ en fonction de $n$. Démontrer cette conjecture.
- En déduire la valeur de la limite $\ell$ de la suite $\left(u_n\right)$.
- Compléter, dans l'annexe 2, l'algorithme permettant de déterminer la valeur du plus petit entier $n$ tel que $\left|u_{n+1} - u_n\right| \leqslant 10^{-3}$.
Annexe 2
$$ \begin{array}{|l |l|}\hline \text{Variables :} &n, a \text{ et } b \text{ sont des nombres.}\\ \text{Initialisation :} & n \text{ prend la valeur } 0\\ &a \text{ prend la valeur } 0\\ &b \text{ prend la valeur } 0,5.\\ \text{Traitement :} & T\text{ ant que } |b - a|\:\:\ldots \ldots.\\ &\hspace{0.8cm}n \text{ prend la valeur }\:\: \ldots \ldots.\\ &\hspace{0.8cm}a \text{ prend la valeur } \:\: \ldots \ldots.\\ &\hspace{0.8cm}b \text{ prend la valeur }\:\: \ldots \ldots.\\ &\text{ Fin Tant que.}\\ \text{Sortie :} &\text{ Afficher }\:\: \ldots \ldots.\\ \hline \end{array} $$
Correction de l'exercice 3 ( 3 points)
La suite $\left(u_n\right)$ est définie par : \[ u_0 = 0 \quad \text{et, pour tout entier naturel }\:n, \:u_{n+1} = \dfrac{1}{2 - u_n}.\]
-
- À l'aide du calcul des premiers termes de la suite $\left(u_n\right)$, conjecturer la forme explicite de $u_n$ en fonction de $n$. Démontrer cette conjecture. En calculant les premiers termes de la suite on obtient :
- En déduire la valeur de la limite $\ell$ de la suite $\left(u_n\right)$. D’après la limite des termes de plus haut degré :
$u_0=0$ $\quad$ $u_1=\dfrac{1}{2}$ $\quad$ $u_2=\dfrac{2}{3}$ $\quad$ $u_3=\dfrac{3}{4}$ $\quad$ $u_4=\dfrac{4}{5}$.
Il semblerait donc que, pour tout entier naturel $n$ on ait $u_n=\dfrac{n}{n+1}$.
Montrons ce résultat par récurrence :
Initialisation : Si $n=0$ $\dfrac{n}{n+1}=\dfrac{0}{1}=0=u_0$.
La propriété est vraie au rang $0$.
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$ : $u_n=\dfrac{n}{n+1}$.
Alors :
$\begin{align*} u_{n+1}&=\dfrac{1}{2-u_n} \\ &=\dfrac{1}{2-\dfrac{n}{n+1}} \\ &=\dfrac{1}{\dfrac{2(n+1)-n}{n+1}} \\ &=\dfrac{1}{\dfrac{2n+2-n}{n+1}} \\ &=\dfrac{1}{\dfrac{n+2}{n+1}} \\ &=\dfrac{n+1}{n+2}
\end{align*}$
La propriété est donc vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$, $u_n=\dfrac{n}{n+1}$.
$\quad$
$\lim\limits_{n \to +\infty} u_n=\lim\limits_{n \to +\infty} \dfrac{n}{n}=1$.
$\quad$ - Compléter, dans l'annexe 2, l'algorithme permettant de déterminer la valeur du plus petit entier $n$ tel que $\left|u_{n+1} - u_n\right| \leqslant 10^{-3}$. On obtient l’algorithme suivant :
Variables :
$\quad$ $n,a$ et $b$ sont des nombres.
Initialisation :
$\quad$ $n$ prend la valeur $0$
$\quad$ $a$ prend la valeur $0$
$\quad$ $b$ prend la valeur $0,5$
Traitement :
$\quad$ Tant que $|b-a| > 10^{-3}$
$\qquad$ $n$ prend la valeur $n+1$
$\qquad$ $a$ prend la valeur $\dfrac{1}{2-a}$
$\qquad$ $b$ prend la valeur $\dfrac{1}{2-b}$
$\quad$ Fin Tant que.
Sortie :
$\quad$ Afficher $n$
$\quad$
Annexe 2
$$ \begin{array}{|l |l|}\hline \text{Variables :} &n, a \text{ et } b \text{ sont des nombres.}\\ \text{Initialisation :} & n \text{ prend la valeur } 0\\ &a \text{ prend la valeur } 0\\ &b \text{ prend la valeur } 0,5.\\ \text{Traitement :} & T\text{ ant que } |b - a|\:\:\ldots \ldots.\\ &\hspace{0.8cm}n \text{ prend la valeur }\:\: \ldots \ldots.\\ &\hspace{0.8cm}a \text{ prend la valeur } \:\: \ldots \ldots.\\ &\hspace{0.8cm}b \text{ prend la valeur }\:\: \ldots \ldots.\\ &\text{ Fin Tant que.}\\ \text{Sortie :} &\text{ Afficher }\:\: \ldots \ldots.\\ \hline \end{array} $$
Exercice 4 4 points
Partie A : un calcul de volume sans repère
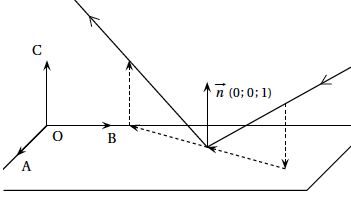
On considère une pyramide équilatère SABCD (pyramide à base carrée dont toutes les faces latérales sont des triangles équilatéraux) représentée ci-contre. Les diagonales du carré ABCD mesurent 24 cm. On note O le centre du carré ABCD. On admettra que OS = OA. 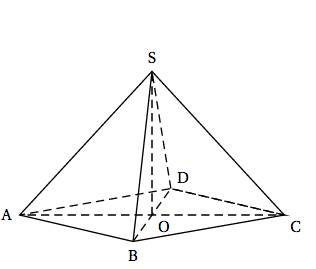
- Sans utiliser de repère, démontrer que la droite (SO) est orthogonale au plan (ABC).
- En déduire le volume, en cm$^3$, de la pyramide SABCD.
Partie B : dans un repère
On considère le repère orthonormé $\left(\text{O}~;~\vec{\text{OA}},~ \vec{\text{OB}}, ~\vec{\text{OS}}\right)$.
- On note P et Q les milieux respectifs des segments [AS] et [BS].
- Justifier que $\vec{n}(1~;~1~;~- 3)$ est un vecteur normal au plan (PQC).
- En déduire une équation cartésienne du plan (PQC).
- Soit H le point du plan (PQC) tel que la droite (SH) est orthogonale au plan (PQC).
- Donner une représentation paramétrique de la droite (SH).
- Calculer les coordonnées du point H.
- Montrer alors que la longueur SH, en unité de longueur, est $\dfrac{2\sqrt{11}}{11}$.
- On admettra que l'aire du quadrilatère PQCD, en unité d'aire, est égale à $\dfrac{3\sqrt{11}}{8}$ Calculer le volume de la pyramide SPQCD, en unité de volume.
Partie C : partage équitable
Pour l'anniversaire de ses deux jumelles Anne et Fanny, Madame Nova a confectionné un joli gâteau en forme de pyramide équilatère dont les diagonales du carré de base mesurent 24 cm. Elle s'apprête à le partager en deux, équitablement, en plaçant son couteau sur le sommet. C'est alors qu'Anne arrête son geste et lui propose une découpe plus originale : «Place la lame sur le milieu d'une arête, parallèlement à un côté de la base, puis coupe en te dirigeant vers le côté opposé ». 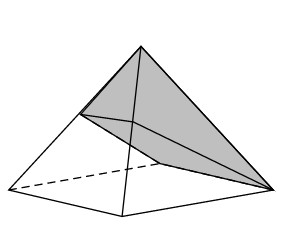
Fanny a des doutes, les parts ne lui semblent pas équitables. Est-ce le cas ? Justifier la réponse.
Correction de l'exercice 4 5 points
Partie A : un calcul de volume sans repère
On considère une pyramide équilatère SABCD (pyramide à base carrée dont toutes les faces latérales sont des triangles équilatéraux) représentée ci-contre. Les diagonales du carré ABCD mesurent 24 cm. On note O le centre du carré ABCD. On admettra que OS = OA. 
- Sans utiliser de repère, démontrer que la droite (SO) est orthogonale au plan (ABC). Les diagonales d’un carré sont de même longueur et se coupent en leur milieu.
- En déduire le volume, en cm$^3$, de la pyramide SABCD. On a $OA=\dfrac{24}{2}=12$ cm.
Par conséquent le triangle $AOB$ est rectangle et $OS=OA=OB$.
Les faces latérales de la pyramide sont des triangles équilatéraux. Par conséquent $AS=AB=BC$.
Dans le triangle $AOB$ rectangle en $O$ on applique le théorème de Pythagore :
$AB^2=AO^2+OB^2 \iff AS^2=OS^2+OA^2$
Ainsi, d’après la réciproque du théorème de Pythagore, le triangle $AOS$ est rectangle en $O$.
On montre de la même façon que le triangle $OSB$ est rectangle en $O$.
La droite $(OS)$ est donc perpendiculaire à deux droites sécantes, $(OA)$ et $(OB)$, du plan $(ABC)$ : elle est orthogonale au plan $(ABC)$.
$\quad$
En reprenant le calcul du théorème de Pythagore dans le triangle $AOB$ de la question précédente on a :
$\begin{align*} AB^2&=AO^2+OB^2 \\ &=12^2+12^2 \\ &=288
\end{align*}$
Par conséquent l’aire du carré $ABCS$ est $\mathscr{A}=AB^2=288$ cm$^2$.
Et le volume de la pyramide $SABCD$ est :
$\mathscr{V}=\dfrac{\mathscr{A}\times SO}{3}=\dfrac{288 \times 12}{3}=1~152$ cm$^3$.
$\quad$
Partie B : dans un repère
On considère le repère orthonormé $\left(\text{O}~;~\vec{\text{OA}},~ \vec{\text{OB}}, ~\vec{\text{OS}}\right)$.
- On note P et Q les milieux respectifs des segments [AS] et [BS].
- Justifier que $\vec{n}(1~;~1~;~- 3)$ est un vecteur normal au plan (PQC). Dans le repère orthonormé $\left(O;\vec{OA},\vec{OB},\vec{OS}\right)$ on a :
- En déduire une équation cartésienne du plan (PQC). Une équation cartésienne du plan $(PQC)$ est donc de la forme $x+y-3z+d=0$.
$O(0,0,0)$, $A(1,0,0)$, $B(0,1,0)$ et $S(0,0,1)$.
Les points $P$ et $Q$ sont les milieux respectifs des segments $[AS]$ et $[BS]$.
Ainsi $P\left(\dfrac{1}{2},0,\dfrac{1}{2}\right)$ et $Q\left(0,\dfrac{1}{2},\dfrac{1}{2}\right)$.
On a également $C(-1,0,0)$ car $\vec{OC}=-\vec{OA}$
Donc $\vec{PQ}\left(-\dfrac{1}{2},\dfrac{1}{2},0\right)$
et $\vec{PC}\left(-\dfrac{3}{2},0,-\dfrac{1}{2}\right)$
Ces deux vecteurs ne sont pas colinéaires car ils n’ont pas la même coordonnée nulle.
Calculons les produits scalaires :
$\vec{n}.\vec{PQ}=-\dfrac{1}{2}+\dfrac{1}{2}-3\times 0 = 0$.
$\vec{n}.\vec{PC}=-\dfrac{3}{2}-3\times \left(-\dfrac{1}{2}\right)=0$.
Le vecteur $\vec{n}$ est donc orthogonal à deux vecteurs non colinéaires du plan $(PQC)$ : il est donc normal à ce plan.
$\quad$
Le point $C$ appartient à ce plan: ses coordonnées vérifient donc cette équation.
Ainsi $-1+0+0+d=0$ soit $d=1$.
Une équation cartésienne du plan $PQC$ est donc $x+y-3z+1=0$. - Soit H le point du plan (PQC) tel que la droite (SH) est orthogonale au plan (PQC).
- Donner une représentation paramétrique de la droite (SH). $\vec{n}$ est un vecteur directeur de la droite $(SH)$.
- Calculer les coordonnées du point H. Le point $H$ est le point d’intersection du plan $(PQC)$ et de la droite $(SH)$.
- Montrer alors que la longueur SH, en unité de longueur, est $\dfrac{2\sqrt{11}}{11}$. Ainsi :
Une représentation paramétrique de la droite $(SH)$ est donc :
$\begin{cases} x=t\\y=t \quad t \in \mathbb R\\z=1-3t\end{cases}$
$\quad$
Ces coordonnées vérifient donc les équations de la droite et du plan.
On a donc :
$\begin{cases} x=t\\y=t\\z=1-3t\\x+y-3z+1=0\end{cases}$
Par conséquent $t+t-3(1-3t)+1=0$
Soit $2t-3+9t+1=0$ d’où $11t=2$ et donc $t=\dfrac{2}{11}$.
Les coordonnées du point $H$ sont donc $\left(\dfrac{2}{11};\dfrac{2}{11};\dfrac{5}{11}\right)$.
$\quad$
$\begin{align*} SH&=\sqrt{\left(\dfrac{2}{11}\right)^2+\left(\dfrac{2}{11}\right)^2+\left(\dfrac{5}{11}-1\right)^2} \\ &=\sqrt{\dfrac{4}{121}+\dfrac{4}{121}+\dfrac{36}{121}} \\ &=\sqrt{\dfrac{44}{121}}\\ &=\dfrac{2\sqrt{11}}{11} \end{align*}$
$\quad$ - On admettra que l'aire du quadrilatère PQCD, en unité d'aire, est égale à $\dfrac{3\sqrt{11}}{8}$ Calculer le volume de la pyramide SPQCD, en unité de volume. Le volume de la pyramide $SPQCD$ est :
$\begin{align*} \mathscr{V}_1&=\dfrac{\dfrac{3\sqrt{11}}{8}\times \dfrac{2\sqrt{11}}{11}}{3} \\ &=\dfrac{1}{4}
\end{align*}$
Le volume de cette pyramide est donc de $0,25$ unité de volume.
$\quad$
Partie C : partage équitable
Pour l'anniversaire de ses deux jumelles Anne et Fanny, Madame Nova a confectionné un joli gâteau en forme de pyramide équilatère dont les diagonales du carré de base mesurent 24 cm. Elle s'apprête à le partager en deux, équitablement, en plaçant son couteau sur le sommet. C'est alors qu'Anne arrête son geste et lui propose une découpe plus originale : «Place la lame sur le milieu d'une arête, parallèlement à un côté de la base, puis coupe en te dirigeant vers le côté opposé ».

Fanny a des doutes, les parts ne lui semblent pas équitables. Est-ce le cas ? Justifier la réponse.
La découpe proposée par Anne revient à obtenir la pyramide $SPQCD$ de la partie précédente.
Le volume, en cm$^3$, de cette pyramide est donné par $12^3\times 0,25=432$ cm$^3$.
Ainsi $\dfrac{432}{1~152}\approx 0,37 \neq 0,5$.
Le partage ne sera donc pas équitable.
$\quad$
Exercice 5 5 points
Dans cet exercice, toutes les probabilités demandées seront arrondies à $10^{-4}$
On étudie un modèle de climatiseur d'automobile composé d'un module mécanique et d'un module électronique. Si un module subit une panne, il est changé.
Partie A : Étude des pannes du module mécanique
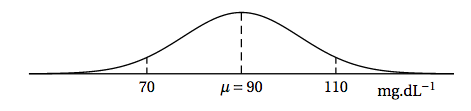
Une enseigne d'entretien automobile a constaté, au moyen d'une étude statistique, que la durée de fonctionnement (en mois) du module mécanique peut être modélisée par une variable aléatoire $D$ qui suit une loi normale d'espérance $\mu = 50$ et d'écart-type $\sigma$ :
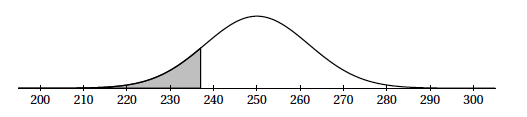
- Déterminer l'arrondi à $10^{-4}$ de $\sigma$ sachant que le service statistique indique que $P(D \geqslant 48) = 0,7977 $.
Pour la suite de cet exercice, on prendra $\sigma = 2,4$ . - Déterminer la probabilité que la durée de fonctionnement du module mécanique soit comprise entre $45$ et $52$ mois.
- Déterminer la probabilité que le module mécanique d'un climatiseur ayant fonctionné depuis $48$ mois fonctionne encore au moins $6$ mois.
Partie B : Étude des pannes d'origine électronique
Sur le même modèle de climatiseur, l'enseigne d'entretien automobile a constaté que la durée de fonctionnement (en mois) du module électronique peut être modélisée par une variable aléatoire $T$ qui suit une loi exponentielle de paramètre $\lambda$.
- Déterminer la valeur exacte de $\lambda$, sachant que le service statistique indique que $P(0 \leqslant T \leqslant 24) = 0,03$.
-
- Déterminer la probabilité que la durée de fonctionnement du module électronique soit comprise entre $24$ et $48$ mois.
-
- Démontrer que, pour tous réels $t$ et $h$ positifs, on a : $P_{T \geqslant t}(T \geqslant t + h) = P(T \geqslant h)$, c'est-à-dire que la variable aléatoire $T$ est sans vieillissement.
- Le module électronique du climatiseur fonctionne depuis $36$ mois. Déterminer la probabilité qu'il fonctionne encore les $12$ mois suivants.
Partie C : Pannes d'origine mécanique et électronique
On admet que les évènements $(D \geqslant 48)$ et $(T \geqslant 48)$ sont indépendants. Déterminer la probabilité que le climatiseur ne subisse aucune panne avant $48$ mois.Partie D : Cas particulier d'un garage de l'enseigne
Un garage de l'enseigne a étudié les fiches d'entretien de $300$ climatiseurs de plus de $4$~ans. Il constate que $246$ d'entre eux ont leur module mécanique en état de fonctionnement depuis $4$ ans. Ce bilan doit-il remettre en cause le résultat donné par le service statistique de l'enseigne, à savoir que $P(D \geqslant 48) = 0,7977 $ ? Justifier la réponse.
Correction Exercice 5 5 points
Dans cet exercice, toutes les probabilités demandées seront arrondies à $10^{-4}$
On étudie un modèle de climatiseur d'automobile composé d'un module mécanique et d'un module électronique. Si un module subit une panne, il est changé.Partie A : Étude des pannes du module mécanique
Une enseigne d'entretien automobile a constaté, au moyen d'une étude statistique, que la durée de fonctionnement (en mois) du module mécanique peut être modélisée par une variable aléatoire $D$ qui suit une loi normale d'espérance $\mu = 50$ et d'écart-type $\sigma$ :- Déterminer l'arrondi à $10^{-4}$ de $\sigma$ sachant que le service statistique indique que $P(D \geqslant 48) = 0,7977 $. $\quad$
- Déterminer la probabilité que la durée de fonctionnement du module mécanique soit comprise entre $45$ et $52$ mois. On veut calculer $P(45 \leq D \leq 52) \approx 0,779~1$
- Déterminer la probabilité que le module mécanique d'un climatiseur ayant fonctionné depuis $48$ mois fonctionne encore au moins $6$ mois. On veut calculer :
$\begin{align*} P(D \geq 48)=0,797~7 &\iff P(D-50\geq -2)=0,797~7 \\ &\iff P\left(\dfrac{D-50}{\sigma} \geq -\dfrac{2}{\sigma}\right)=0,797~7 \\ &\iff P\left(\dfrac{D-50}{\sigma} \leq -\dfrac{2}{\sigma}\right)=0,202~3
\end{align*}$
La variable aléatoire $\dfrac{D-50}{\sigma}$ suit la loi normale centrée réduite.
En utilisant la fonction inverse loi normale de la calculatrice on obtient :
$-\dfrac{2}{\sigma} \approx -0,833~4 \iff \sigma \approx 2,399~8$.
$\quad$
2ND DISTR 3Fracnormale( $\1 $ )EXE
Avec une calculatrice de type TI$$Fracnormale( \1 ) \approx \2$$
$$\pi^{-1}( \1)\approx \2 \text{ à } 10^{-\3} \text{ près.}$$Pour la suite de cet exercice, on prendra $\sigma = 2,4$ .
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
$$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$
$\begin{align*} P_{(D \geq 48)}(D\geq 54)&=\dfrac{P(\geq 54)}{P(D\geq 48)} \\ &=\dfrac{0,5-P(50 \leq D\leq 54)}{0,5+P(48 \leq D\leq 50)} \\ &\approx 0,059~9
\end{align*}$
Remarque : $(D\geq 48)\cap(D\geq 54)=(D\geq 54)$.Partie B : Étude des pannes d'origine électronique
Sur le même modèle de climatiseur, l'enseigne d'entretien automobile a constaté que la durée de fonctionnement (en mois) du module électronique peut être modélisée par une variable aléatoire $T$ qui suit une loi exponentielle de paramètre $\lambda$.- Déterminer la valeur exacte de $\lambda$, sachant que le service statistique indique que $P(0 \leqslant T \leqslant 24) = 0,03$. $\quad$
-
- Déterminer la probabilité que la durée de fonctionnement du module électronique soit comprise entre $24$ et $48$ mois. On veut calculer :
-
- Démontrer que, pour tous réels $t$ et $h$ positifs, on a : $P_{T \geqslant t}(T \geqslant t + h) = P(T \geqslant h)$, c'est-à-dire que la variable aléatoire $T$ est sans vieillissement.
- Le module électronique du climatiseur fonctionne depuis $36$ mois. Déterminer la probabilité qu'il fonctionne encore les $12$ mois suivants. On veut calculer :
$\begin{align*} P_{T\geq t}(T \geq t+h)&=\dfrac{P\left(T\geq t)\cap (T\geq t+h)\right)}{P(T\geq t)} \\ &=\dfrac{P(T\geq t+h)}{P(T\geq t)} \\ &=\dfrac{\text{e}^{-(t+h)\lambda}}{\text{e}^{-t\lambda}}\\ &=\text{e}^{-h\lambda}\\ &P(T \geq h)
\end{align*}$
$\quad$
$\begin{align*} P_{T \geq 36}(T \geq 36+12) &=P(T\geq 12) \quad \text{ cf B.3.a} \\ &=\text{e}^{-12\times 0,001~27}\\ &\approx 0,984~9
\end{align*}$
$\begin{align*} P(24 \leq T \leq 48)&=\text{e}^{-0,001~27\times 24}-\text{e}^{-0,001~27\times 48} \\ &\approx 0,029~1
\end{align*}$
$\quad$Partie C : Pannes d'origine mécanique et électronique
On admet que les évènements $(D \geqslant 48)$ et $(T \geqslant 48)$ sont indépendants. Déterminer la probabilité que le climatiseur ne subisse aucune panne avant $48$ mois.On veut calculer :
$\begin{align*} P\left((D \geq 48)\cap (T\geq 48)\right)&=P(D \geq 48)\times P(T \geq 48) \quad \text{indépendance} \\ &=0,797~7 \times \text{e}^{-0,001~27\times 48} \\ & \approx 0,7505
\end{align*}$
$\quad$Partie D : Cas particulier d'un garage de l'enseigne
Un garage de l'enseigne a étudié les fiches d'entretien de $300$ climatiseurs de plus de $4$~ans. Il constate que $246$ d'entre eux ont leur module mécanique en état de fonctionnement depuis $4$ ans. Ce bilan doit-il remettre en cause le résultat donné par le service statistique de l'enseigne, à savoir que $P(D \geqslant 48) = 0,7977 $ ? Justifier la réponse.La proportion $p$ est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times p $=\3 et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.En effet on a bien : $$n \geq 30\;;\; n \times p \geq 5 \text{ et } n\times (1-p) \geq 5$$
$$I_{300}[0,732~8;0,843~2] $$
L'intervalle de fluctuation asymptotique au seuil de $95\% $ est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$La fréquence observée est $f=\dfrac{246}{300}=0,82 \in I_{300}$
Cela ne remet donc pas en cause, au risque de $5\%$, le résultat donné par le service statistique de l’enseigne.
$\quad$
Spécialité 5 points
Les entiers naturels 1, 11, 111, 1111 , $\ldots$ sont des rep-units. On appelle ainsi les entiers naturels ne s'écrivant qu'avec des 1. Pour tout entier naturel $p$ non nul, on note $N_p$ le rep-unit s'écrivant avec $p$ fois le chiffre 1 : \[N_p = \underbrace{11 \ldots 1}_{\begin{array}{c}\tiny p {} \text{répétitions} \\ \tiny \text{du chiffre }1 \end{array}} = \displaystyle\sum_{k=0}^{k=p-1} 10^k.\] Dans tout l'exercice, $p$ désigne un entier naturel non nul. L'objet de cet exercice est d'étudier quelques propriétés des rep-units.
Partie A : divisibilité des rep-units dans quelques cas particuliers
- Montrer que $N_p$ n'est divisible ni par 2 ni par 5.
- Dans cette question, on étudie la divisibilité de $N_p$ par 3.
- Prouver que, pour tout entier naturel $j$, $10^j \equiv 1 \:\:\text{mod } 3$.
- En déduire que $N_p \equiv p \:\:\text{mod } 3$.
- Déterminer une condition nécessaire et suffisante pour que le rep-unit $N_p$ soit divisible par 3.
- Dans cette question, on étudie la divisibilité de $N_p$ par $7$.
- Recopier et compléter le tableau de congruences ci-dessous, où $a$ est l'unique entier relatif appartenant à $\{-3~;~-2~;~- 1~;~0~;~1~;~2~;~3\}$ tel que $10^m \equiv a \:\:\text{mod}\: \:7$.
On ne demande pas de justification. $$\begin{array} {|c|c|c|c|c|c|c|c|}\hline m &0 &1 &2 &3 &4 &5 &6\\ \hline a & & & & & & &\\ \hline \end{array}$$ - Soit $p$ un entier naturel non nul. Montrer que $10^p \equiv 1 \:\:\text{mod}\: 7$ si et seulement si $p$ est un multiple de $6$.
On pourra utiliser la division euclidienne de $p$ par $6$. - Justifier que, pour tout entier nature $p$ non nul, $N_p = \dfrac{10^p - 1}{9}$.
- Démontrer que « 7 divise $N_p$ » est équivalent à « 7 divise $9N_p$ ».
- En déduire que $N_p$ est divisible par 7 si et seulement si $p$ est un multiple de 6.
- Recopier et compléter le tableau de congruences ci-dessous, où $a$ est l'unique entier relatif appartenant à $\{-3~;~-2~;~- 1~;~0~;~1~;~2~;~3\}$ tel que $10^m \equiv a \:\:\text{mod}\: \:7$.
Partie B : un rep-unit strictement supérieur à 1 n'est jamais un carré parfait
- Soit $n$ un entier naturel supérieur ou égal à $2$. On suppose que l'écriture décimale de $n^2$ se termine par le chiffre 1, c'est-à-dire $n^2 \equiv 1 \:\:\text{mod}\: 10$.
- Recopier et compléter le tableau de congruences ci-dessous. $$ \begin{array}{| c|c|c|c|c|c|c|c|c|c|}\hline n \equiv \ldots \ \ [10] & 0 & 1 & 2 & 3 & 4 &5 & 6 & 7 & 8 & 9 \\ \hline n^2 \equiv \ldots \ \ [10] &&&&&&&&&&\\ \hline \end{array} $$
- En déduire qu'il existe un entier naturel $m$ tel que: $n = 10m + 1$ ou $n = 10m - 1$.
- Conclure que $n^2 \equiv 1 \:\: \text{mod}\: 20$.
- Soit $p$ un entier naturel supérieur ou égal à 2. Quel est le reste de la division euclidienne de $N_p$ par 20 ?
- En déduire que, pour $p$ entier naturel supérieur ou égal à 2, le rep-unit $N_p$ n'est pas le carré d'un entier.
$\begin{align*} P(0\leq T\leq 24)=0,03 &\iff 1-\text{e}^{-24\lambda} = 0,03 \\ &\iff \text{e}^{-24\lambda}=0,97 \\ &\iff -24\lambda = \ln 0,97 \\ &\iff \lambda = -\dfrac{\ln 0,97}{24}
\end{align*}$
$\quad$Pour la suite de cet exercice, on prendra $\lambda = 0,00127 $ .
Pour la suite de cet exercice, on prendra $\lambda = 0,00127 $ .
Correction de l'exercice de Spécialité 5 points
Les entiers naturels 1, 11, 111, 1111 , $\ldots$ sont des rep-units. On appelle ainsi les entiers naturels ne s'écrivant qu'avec des 1. Pour tout entier naturel $p$ non nul, on note $N_p$ le rep-unit s'écrivant avec $p$ fois le chiffre 1 : \[N_p = \underbrace{11 \ldots 1}_{\begin{array}{c}\tiny p {} \text{répétitions} \\ \tiny \text{du chiffre }1 \end{array}} = \displaystyle\sum_{k=0}^{k=p-1} 10^k.\] Dans tout l'exercice, $p$ désigne un entier naturel non nul. L'objet de cet exercice est d'étudier quelques propriétés des rep-units.
Partie A : divisibilité des rep-units dans quelques cas particuliers
- Montrer que $N_p$ n'est divisible ni par 2 ni par 5. Le chiffre des unités de $N_p$ est $1$.
- Dans cette question, on étudie la divisibilité de $N_p$ par 3.
- Prouver que, pour tout entier naturel $j$, $10^j \equiv 1 \:\:\text{mod } 3$. $10\equiv 1$ mod $3$ donc pour tout entier naturel $j$ on a $10^j \equiv 1$ mod $3$.
- En déduire que $N_p \equiv p \:\:\text{mod } 3$. $\displaystyle \sum_{k=0}^{k=p-1} 10^k \equiv \sum_{k=0}^{k=p-1} 1$ mod $3$ $\equiv p$ mod $3$.
- Déterminer une condition nécessaire et suffisante pour que le rep-unit $N_p$ soit divisible par 3. $N_p$ est divisible par $3$ si, et seulement si, $p$ mod $3 = 0$ c’est-à-dire si, et seulement si, $p$ est un multiple de $3$.
$\quad$
$\quad$
- Dans cette question, on étudie la divisibilité de $N_p$ par $7$.
- Recopier et compléter le tableau de congruences ci-dessous, où $a$ est l'unique entier relatif appartenant à $\{-3~;~-2~;~- 1~;~0~;~1~;~2~;~3\}$ tel que $10^m \equiv a \:\:\text{mod}\: \:7$.
On ne demande pas de justification. $$\begin{array} {|c|c|c|c|c|c|c|c|}\hline m &0 &1 &2 &3 &4 &5 &6\\ \hline a & & & & & & &\\ \hline \end{array}$$ $$\begin{array}{|c|c|c|c|c|c|c|c|} \hline m&0&1&2&3&4&5&6 \\ \hline a&1&3&2&-1&-3&-2&1\\ \hline \end{array}$$ - Soit $p$ un entier naturel non nul. Montrer que $10^p \equiv 1 \:\:\text{mod}\: 7$ si et seulement si $p$ est un multiple de $6$.
On pourra utiliser la division euclidienne de $p$ par $6$. - Justifier que, pour tout entier nature $p$ non nul, $N_p = \dfrac{10^p - 1}{9}$. Pour tout entier naturel $p$ non nul, $N_p$ est la somme des $p$ premiers termes de la suite géométrique de premier terme $1$ et de raison $10$.
- Démontrer que « 7 divise $N_p$ » est équivalent à « 7 divise $9N_p$ ». $7$ et $9$ sont premiers entre eux donc, d’après le théorème de Gauss, $7$ divise $N_p$ est équivalent à $7$ divise $9N_p$.
- En déduire que $N_p$ est divisible par 7 si et seulement si $p$ est un multiple de 6. $\begin{align*} N_p \equiv 0 \text{ mod } 7&\iff 9N_p\equiv 0 \text{ mod } 7 \\ &\iff 10^p-1 \equiv 0 \text{ mod } 7 \\ &\iff 10^p \equiv 1 \text{ mod } 7\\ &\iff p \equiv 0 \text{ mod } 6
$\quad$
On a $p=6q+r$ ou $q$ est un entier relatif et $q$ un entier naturel strictement inférieur à $6$.
Ainsi $10^p=\left(10^6\right)^q\times 10^r \equiv 1^q\times 10^r$ mod $7$.
D’après le tableau précédent $10^p\equiv 1$ mod $7$ si, et seulement si, $p=0$ ou $p=6$.
Ainsi $10^p \equiv 1$ mod $7$ si, et seulement si, $r=0$ c’est-à-dire si, et seulement si, $p$ est un multiple de $6$.
$\quad$
Ainsi $N_p=\dfrac{1-10^p}{1-10}=\dfrac{10^p-1}{9}$.
$\quad$
$\quad$
\end{align*}$
Donc $N_p$ est divisible par $7$ si, et seulement si, $p$ est un multiple de $6$. - Recopier et compléter le tableau de congruences ci-dessous, où $a$ est l'unique entier relatif appartenant à $\{-3~;~-2~;~- 1~;~0~;~1~;~2~;~3\}$ tel que $10^m \equiv a \:\:\text{mod}\: \:7$.
Un nombre est divisible par $2$ si son chiffre des unités est pair.
Un nombre est divisible par $5$ si son chiffre des unités est $0$ ou $5$.
Par conséquent $N_p$ n’est divisible ni par $2$ ni par $5$.
Partie B : un rep-unit strictement supérieur à 1 n'est jamais un carré parfait
- Soit $n$ un entier naturel supérieur ou égal à $2$. On suppose que l'écriture décimale de $n^2$ se termine par le chiffre 1, c'est-à-dire $n^2 \equiv 1 \:\:\text{mod}\: 10$.
- Recopier et compléter le tableau de congruences ci-dessous. $$ \begin{array}{| c|c|c|c|c|c|c|c|c|c|}\hline n \equiv \ldots \ \ [10] & 0 & 1 & 2 & 3 & 4 &5 & 6 & 7 & 8 & 9 \\ \hline n^2 \equiv \ldots \ \ [10] &&&&&&&&&&\\ \hline \end{array} $$ $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline
- En déduire qu'il existe un entier naturel $m$ tel que: $n = 10m + 1$ ou $n = 10m - 1$. Le chiffre des unités de $n^2$ se termine par le chiffre $1$ si, et seulement si, le chiffre des unités de $n$ se termine par $1$ ou par $9$.
- Conclure que $n^2 \equiv 1 \:\: \text{mod}\: 20$. Si $n=10m+1$ alors $n^2=100m^2+20m+1 \equiv 1$ mod $20$.
n\equiv \ldots ~[10]&0&1&2&3&4&5&6&7&8&9 \\ \hline n^2=\ldots ~[10]&0&1&4&9&6&5&6&9&4&1\\ \hline \end{array}$$
Or $9\equiv -1$ mod $10$
Cela signifie donc qu’il existe un entier naturel $m$ tel que $n=10m+1$ ou $n=10m-1$.
Si $n=10m-1$ alors $n^2=100m^2-20m+1\equiv 1$ mod $20$.
Dans tous les cas $n^2\equiv 1$ mod $20$.
$\quad$ - Soit $p$ un entier naturel supérieur ou égal à 2. Quel est le reste de la division euclidienne de $N_p$ par 20 ? Si $n\geq 2$ alors $N_p=\underbrace{11\ldots 1}_{p-2 \text{ fois}}00+11=100\displaystyle \sum_{k=2}^{k=p-1}10^{k-2}+11 \equiv 11$ mod $20$
- En déduire que, pour $p$ entier naturel supérieur ou égal à 2, le rep-unit $N_p$ n'est pas le carré d'un entier. D’après la question B.1.c. si $n^2 \equiv 1$ mod $10$ alors $n^2 \equiv 1$ mod $20$.
$\quad$
Or $N_p\equiv 1$ mod $10$ et $N_p \equiv 11$ mod $20$.
Donc $N_p$ n’est pas le carré d’un entier.
- Vues: 54294