Baccalauréat STI 2D/STL spécialité SPCL Métropole 11 septembre 2014

Exercice 1 5 points

QCM

Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée.
Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point.

Indiquer sur la copie le numéro de la question et la réponse correspondante.

1. La forme exponentielle du nombre complexe $z_{1} = \sqrt{6} + \text{i}\sqrt{6}$ est :
   1. $z_{1} = 2\sqrt{3}\text{e}^{\text{i}\frac{\pi}{4}}$
   2. $z_{1} = 2\sqrt{6}\text{e}^{-\text{i}\frac{\pi}{4}}$
   3. $z_{1} = 6\text{e}^{\text{i}\frac{\pi}{4}}$
   4. $z_{1} = \sqrt{2}\text{e}^{\text{i}\frac{7\pi}{4}}$
2. On considère les nombres complexes $z_{1} = \sqrt{6} + \text{i}\sqrt{6}$ et $z_{2} = - \sqrt{6} + \text{i}\sqrt{6}$. Le nombre complexe $z_{2}$ est égal à :
   1. $\overline{z_{1}}$
   2. $- z_{1}$
   3. $- \overline{z_{1}}$
   4. $\text{i} + z_{1}$
3. La fonction $f$ est définie sur l'intervalle $]0 ; +\infty[$ par $f(x) = \dfrac{1}{x}$. Sa courbe représentative est donnée ci-dessous :
   
   Le domaine du plan défini comme l'ensemble des points $M$ de coordonnées $(x ; y)$ qui vérifient $1 \leqslant x \leqslant 2$ et $\dfrac{1}{x} \leqslant y \leqslant 1$ a pour aire (exprimée en unité d'aire) :
   1. $\ln 2$
   2. $\dfrac{1}{2}$
   3. $1 - \ln 2$
   4. $1 - \text{e}^2$
4. La tangente au point d'abscisse $\dfrac{1}{2}$ à la courbe représentative de la fonction $f$, définie sur l'intervalle $]0 ; + \infty[$ par $f(x) = \dfrac{1}{x}$, a pour équation :
   1. $y = - 4x + 4$
   2. $y = \phantom{-}4x + 4$
   3. $y = - 4x - 4$
   4. $y = \phantom{-}4x - 4$

Correction de l'exercice 1 (5 points)

QCM

Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée.
Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point.

Indiquer sur la copie le numéro de la question et la réponse correspondante.

1. La forme exponentielle du nombre complexe $z_{1} = \sqrt{6} + \text{i}\sqrt{6}$ est :
   1. $z_{1} = 2\sqrt{3}\text{e}^{\text{i}\frac{\pi}{4}}$
   2. $z_{1} = 2\sqrt{6}\text{e}^{-\text{i}\frac{\pi}{4}}$
   3. $z_{1} = 6\text{e}^{\text{i}\frac{\pi}{4}}$
   4. $z_{1} = \sqrt{2}\text{e}^{\text{i}\frac{7\pi}{4}}$
Forme trigonométrique de $z_1=\sqrt{6} + \text{i}\sqrt{6}$:
Module : $|z_1|=\sqrt{a^2+b^2}=\sqrt{\sqrt{6}^2+\sqrt{6}^2}=\sqrt{12}=2\sqrt{3}$
Argument: $$\left\{ \begin{array}{l } \cos(\theta)=\dfrac{a}{r}= \dfrac{\sqrt{6}}{2\sqrt{3}}= \dfrac{\sqrt 2}{2} \\ \sin(\theta)=\dfrac{b}{r}= \dfrac{\sqrt{6}}{2\sqrt{3}}= \dfrac{\sqrt2}{ 2} \end{array} \right.$$ Ainsi $\theta=\dfrac{\pi}{4}$ convient; on a donc: $$z_1=[2\sqrt{3};\dfrac{\pi}{4}] \text{ ou } z_1=2\sqrt{3}\left [\cos\left (\dfrac{\pi}{4}\right )+i\sin\left (\dfrac{\pi}{4}\right )\right ]$$
La forme exponentielle de $z_{1}$ est $z_1= 2\sqrt{3}e^{i\frac{\pi}{4}}$
2. On considère les nombres complexes $z_{1} = \sqrt{6} + \text{i}\sqrt{6}$ et $z_{2} = - \sqrt{6} + \text{i}\sqrt{6}$. Le nombre complexe $z_{2}$ est égal à :
   1. $\overline{z_{1}}$
   2. $- z_{1}$
   3. $- \overline{z_{1}}$
   4. $\text{i} + z_{1}$
$$z_2=-\left(\sqrt{6} - \text{i}\sqrt{6}\right)=- \overline{z_{1}}$$
$z_2=-\overline{z_1}$
3. La fonction $f$ est définie sur l'intervalle $]0 ; +\infty[$ par $f(x) = \dfrac{1}{x}$. Sa courbe représentative est donnée ci-dessous :
   
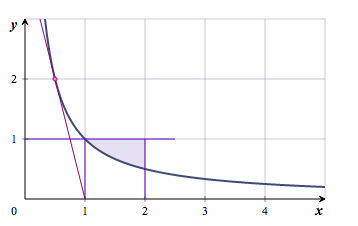
   Le domaine du plan défini comme l'ensemble des points $M$ de coordonnées $(x ; y)$ qui vérifient $1 \leqslant x \leqslant 2$ et $\dfrac{1}{x} \leqslant y \leqslant 1$ a pour aire (exprimée en unité d'aire) :
   1. $\ln 2$
   2. $\dfrac{1}{2}$
   3. $1 - \ln 2$
   4. $1 - \text{e}^2$
Le domaine du plan défini comme l'ensemble des points $M$ de coordonnées $(x;y)$ qui vérifient $1⩽x⩽2$ et $\dfrac{1}{x}\leq y\leq1$ est le domaine du plan compris entre la droite d'équation $y=1$ , la courbe représentative de la fonction $f$ et les droites d'équation $x=1$ et $x=2$ . L'aire, exprimée en unité d'aire, de ce domaine est donc égale à la différence entre l'aire du carré de côté 1 et l’intégrale de la fonction $f$ sur l'intervalle $[1;2]$ : $$\begin{array}{ll} \mathcal{A}&= 1 -\int_1^2 \dfrac{1}{x} \; dx\\ &= 1- \left[ \ln x \right]_1^2\\ &= 1-\left( \ln 2-\ln 1 \right)\\ &= 1 -\ln 2\end{array}$$
$\mathcal{A} =1-\ln 2$
4. La tangente au point d'abscisse $\dfrac{1}{2}$ à la courbe représentative de la fonction $f$, définie sur l'intervalle $]0 ; + \infty[$ par $f(x) = \dfrac{1}{x}$, a pour équation :
   1. $y = - 4x + 4$
   2. $y = \phantom{-}4x + 4$
   3. $y = - 4x - 4$
   4. $y = \phantom{-}4x - 4$
La tangente au point d'abscisse $\dfrac{1}{2}$ à la courbe représentative de la fonction $f$ a pour équation : $$y=f’\left(\dfrac{1}{2}\right)\times \left(x−\dfrac{1}{2}\right)+f\left(\dfrac{1}{2}\right)$$ Or $f’$ est la fonction définie sur l'intervalle $]0;+\infty[$ par $f'(x)=−\dfrac{1}{x^2}$ d'où $f’\left(\dfrac{1}{2}\right)=-4$. D'autre part, $f\left(\dfrac{1}{2}\right)=2$. Donc la tangente au point d'abscisse $\dfrac{1}{2}$ à la courbe représentative de la fonction $f$ a pour équation : $$y=-4\times \left(x−\dfrac{1}{2}\right)+2\iff y=-4x+4$$
Donc la tangente au point d'abscisse $\dfrac{1}{2}$ à la courbe représentative de la fonction $f$ a pour équation :$y=-4x+4$

Exercice 2 5 points

Fonction ln

Une équipe aérospatiale se propose d'envoyer un satellite de $10$ tonnes en orbite autour de la Terre par l'intermédiaire d'une fusée à un seul étage. Cette fusée a une masse à vide, c'est-à-dire sans carburant ni satellite, de $40$ tonnes. L'éjection des gaz permet à la fusée de décoller et de s'élever dans les airs jusqu'à la consommation totale du propergol, carburant contenu dans ses réservoirs. La vitesse d'éjection des gaz est $V_{\text{e}} = 3200$ m.s$^{-1}$. La vitesse finale de la fusée vitesse atteinte lorsque les réservoirs sont vides, varie en fonction de la masse de propergol contenue au départ dans les réservoirs. Elle doit être de $8000$ m.s$^{-1}$ pour permettre la mise en orbite souhaitée. Le but de l'exercice est de déterminer la masse de propergol à mettre dans les réservoirs pour permettre cette mise en orbite du satellite. On note $x$ la masse, en tonnes, de propergol contenu au décollage dans les réservoirs de la fusée. La masse $x$ est comprise entre 100 et 900 tonnes. La masse totale de la fusée est alors $(x + 50)$ tonnes. Il est établi que la vitesse finale de la fusée, $f(x)$, exprimée en m· s$^{-1}$, est donnée par $$f(x) = V_{\text{e}} \times [\ln(x + 50) - \ln 50]$$ où $x$ est un réel de l'intervalle [100 ; 900].

1. Montrer que, pour tout réel $x$ de l'intervalle [100 ; 900], $f(x) = 3200 \times \ln (0,02x + 1)$. On pourra choisir l'une ou l'autre des expressions de $f(x)$ pour répondre à chacune des questions suivantes.
2. 1. Si les réservoirs contiennent au décollage 100 tonnes de propergol, quelle sera la vitesse finale de la fusée ?
   2. Avec 400 tonnes de propergol au décollage la mise en orbite sera-t-elle possible ?
3. 1. Calculer la fonction dérivée $f'$ de la fonction $f$.
   2. En déduire le sens de variation de la fonction $f$.
4. Déterminer la masse de propergol à mettre dans les réservoirs pour permettre la mise en orbite souhaitée.

Correction de l'exercice 2 (5 points)

Fonction ln

Une équipe aérospatiale se propose d'envoyer un satellite de $10$ tonnes en orbite autour de la Terre par l'intermédiaire d'une fusée à un seul étage. Cette fusée a une masse à vide, c'est-à-dire sans carburant ni satellite, de $40$ tonnes. L'éjection des gaz permet à la fusée de décoller et de s'élever dans les airs jusqu'à la consommation totale du propergol, carburant contenu dans ses réservoirs. La vitesse d'éjection des gaz est $V_{\text{e}} = 3200$ m.s$^{-1}$. La vitesse finale de la fusée vitesse atteinte lorsque les réservoirs sont vides, varie en fonction de la masse de propergol contenue au départ dans les réservoirs. Elle doit être de $8000$ m.s$^{-1}$ pour permettre la mise en orbite souhaitée. Le but de l'exercice est de déterminer la masse de propergol à mettre dans les réservoirs pour permettre cette mise en orbite du satellite. On note $x$ la masse, en tonnes, de propergol contenu au décollage dans les réservoirs de la fusée. La masse $x$ est comprise entre 100 et 900 tonnes. La masse totale de la fusée est alors $(x + 50)$ tonnes. Il est établi que la vitesse finale de la fusée, $f(x)$, exprimée en m· s$^{-1}$, est donnée par $$f(x) = V_{\text{e}} \times [\ln(x + 50) - \ln 50]$$ où $x$ est un réel de l'intervalle [100 ; 900].

1. Montrer que, pour tout réel $x$ de l'intervalle [100 ; 900], $f(x) = 3200 \times \ln (0,02x + 1)$. On pourra choisir l'une ou l'autre des expressions de $f(x)$ pour répondre à chacune des questions suivantes.
$f(x)=V_e\times \left[\ln(x+50)−\ln50\right]$ avec $Ve=3200m.s^{-1}$ d'où : $$\begin{array}{ll} f(x)&= 3200\times \left[\ln(x+50)−\ln50\right]\\ &=3200\times \ln\left(\dfrac{x+50}{50}\right)\\ & =3200\times \ln(0,02x+1) \end{array}$$
$f$ est la fonction définie pour tout réel $x$ de l'intervalle $[100;900]$ par $f(x)=3200\times \ln(0,02x+1).$
2. 1. Si les réservoirs contiennent au décollage 100 tonnes de propergol, quelle sera la vitesse finale de la fusée ?
   $f(100)=3200\times\ln 3\approx 3515,6$
   Avec 100 tonnes de propergol au décollage, la vitesse finale de la fusée sera d'environ $3516m.s^{-1}.$
   2. Avec 400 tonnes de propergol au décollage la mise en orbite sera-t-elle possible ?
   $f(400)=3200\times \ln9\approx 7031,1$
   Avec 400 tonnes de propergol au décollage, la vitesse finale de la fusée ne permettra pas la mise en orbite du satellite.
3. 1. Calculer la fonction dérivée $f'$ de la fonction $f$.
   $$\begin{array}{ll} f’(x)&= 3200\times \dfrac{0,02}{0,02x+1}\\ &\dfrac{64}{0,02x+1}\\ \end{array}$$
   $f’$ est la fonction définie pour tout réel $x$ de l'intervalle $[100;900]$ par $f’(x)=\dfrac{64}{0,02x+1}.$
   2. En déduire le sens de variation de la fonction $f$.
   Pour tout réel $x$ de l'intervalle $[100;900]$, $0,02x+1>0$ donc $f’(x)>0$.
   La dérivée $f’$ est positive sur l'intervalle $[100;900]$ donc la fonction $f$ est croissante.
4. Déterminer la masse de propergol à mettre dans les réservoirs pour permettre la mise en orbite souhaitée.
$$\begin{array}{ll} 3200\times \ln(0,02x+1)=8000&\iff \ln(0,02x+1)=2,5\\ &\iff 0,02x+1=e^{2,5}\\ &\iff 0,02x=e^{2,5}-1\\ &\iff x=\dfrac{e^{2,5}-1}{0,02}\\ &\iff x=50\left(e^{2,5}-1\right)\\ \end{array}$$ Comme $50\left(e^{2,5}-1\right)\approx 559,1$ et que la fonction $f$ est croissante :
$560$ tonnes de de propergol sont nécessaires pour permettre la mise en orbite du satellite.

Exercice 3 5 points

Suites

Chloé, âgée de 15 ans au 1er janvier 2014, réside dans une agglomération française. Pour anticiper le financement de son permis de conduire, elle décide de placer sur un produit d'épargne ses $600$ euros d'économies à partir du 1er janvier 2014.

Information 1 : conditions de souscription du livret jeune

• Montant maximum de placement: 1600 euros
• Taux d'intérêt annuel de 2,75$\,\%$
• Avoir entre 12 et 25 ans
• Montant minimum à l'ouverture : 10 euros
• Résider en France

Information 2 : coût moyen du permis de conduire

• La loi impose un minimum de $20$ heures de conduite avant de se présenter au permis.
• Une enquête de la CLCV (Consommation, Logement et Cadre de Vie) publiée en août 2013 et menée auprès de $447$ auto-écoles souligne que ce forfait de $20$ heures est facturé du simple au double selon les régions.
• Par ailleurs, même si le minimum imposé par la loi est de vingt heures de conduite, il en faut plutôt trente en moyenne.
• Ainsi, en comptant les frais de dossier, il est préférable de prévoir un budget de 1500 euros.

Partie A

1. Expliquer pourquoi Chloé remplit les conditions permettant de souscrire au livret jeune.
2. Aura-t-elle une somme suffisante disponible au 1er janvier 2017 pour passer son permis si elle choisit de souscrire au livret jeune ?

Partie B

Chloé aura besoin de 1500 euros pour financer son permis. Ses parents lui conseillent de verser chaque mois sur le livret la somme supplémentaire de 25 euros, à partir du 1er février 2014. Ils lui expliquent que le taux annuel du livret jeune correspond à un taux mensuel de 0,226$\,\%$.

1. Ses parents lui présentent un extrait d'une page de tableur qui simule l'évolution d'épargne : $$\begin{array}{|c|c|} \hline &A& B\\ \hline 1 &01/01/2014 &600,00 \text{€}\\ \hline 2 &01/02/2014 &626,36 \text{€}\\ \hline 3 &01/03/2014 &652,77 \text{€}\\ \hline 4 &01/04/2014 &679,25 \text{€}\\ \hline 5 &01/05/2014 &705,78 \text{€}\\ \hline 6 &01/06/2014 &732,38 \text{€}\\ \hline 7 &... &...\\ \hline \end{array}$$
   1. Justifier que, dans la feuille de calcul ci-dessus, la formule à saisir dans la cellule $B2$ est
      
        $=  1,00226 \times \text{B}1 + 25$.
   2. Déterminer la somme qui serait disponible sur le livret au 1er juillet 2014.
2. Chloé veut déterminer au bout de combien de mois elle aurait l'argent nécessaire pour financer son permis en suivant le conseil de ses parents. Elle décide de noter $u_{n}$ la somme, en euros, disponible le $n$-ième mois après l'ouverture du livret. Ainsi, $u_{0}$ vaut 600 euros.
   1. Exprimer $u_{n+1}$ en fonction de $u_{n}$.
   2. Chloé décide d'écrire l'algorithme suivant : $$\begin{array}{|ll|}\hline\text{Variables}\\ \hspace{0,3cm}n :\text{ un nombre entier naturel}\\ \hspace{0,3cm}u : \text{ un nombre réel }\\\text{Initialisation}\\ \hspace{0,3cm}\text{ Affecter à } n \text{ la valeur } 0\\ \hspace{0,3cm}\text{ Affecter à } u \text{ la valeur } 600\\\text{Traitement}\\ \hspace{0,3cm} \text{ Tant que }\ldots\ldots\\ \hspace{0,6cm}\text{ Affecter à } n \text{ la valeur } n + 1\\ \hspace{0,6cm}\text{ Affecter à } u \text{ la valeur }\ldots\ldots\\ \hspace{0,3cm}\text{ Fin Tant que }\\\text{Sortie}\\ \hspace{0,3cm}\text{ Afficher }\ldots\\ \hline \end{array}$$ Trois lignes de l'algorithme comportent des pointillés. Recopier ces lignes et les compléter pour que Chloé puisse déterminer le nombre de mois cherché.
   3. Au bout de combien de mois Chloé aura-t-elle l'argent nécessaire pour financer son permis si elle suit les conseils de ses parents ?

Correction de l'exercice 3 (5 points)

Suites

Chloé, âgée de 15 ans au 1er janvier 2014, réside dans une agglomération française. Pour anticiper le financement de son permis de conduire, elle décide de placer sur un produit d'épargne ses $600$ euros d'économies à partir du 1er janvier 2014.

Information 1 : conditions de souscription du livret jeune

• Montant maximum de placement: 1600 euros
• Taux d'intérêt annuel de 2,75$\,\%$
• Avoir entre 12 et 25 ans
• Montant minimum à l'ouverture : 10 euros
• Résider en France

Information 2 : coût moyen du permis de conduire

• La loi impose un minimum de $20$ heures de conduite avant de se présenter au permis.
• Une enquête de la CLCV (Consommation, Logement et Cadre de Vie) publiée en août 2013 et menée auprès de $447$ auto-écoles souligne que ce forfait de $20$ heures est facturé du simple au double selon les régions.
• Par ailleurs, même si le minimum imposé par la loi est de vingt heures de conduite, il en faut plutôt trente en moyenne.
• Ainsi, en comptant les frais de dossier, il est préférable de prévoir un budget de 1500 euros.

Partie A

1. Expliquer pourquoi Chloé remplit les conditions permettant de souscrire au livret jeune.
Chloé, âgée de 15 ans au 1er janvier 2014, réside dans une agglomération française et verse 600 euros. Chloé remplit les conditions permettant de souscrire au livret jeune.
2. Aura-t-elle une somme suffisante disponible au 1er janvier 2017 pour passer son permis si elle choisit de souscrire au livret jeune ?
Soit $C_n$ le capital disponible le 1er janvier de l'année $(2014+n)$.
Le taux d'intérêt annuel étant de $2,75\ %$, on a :
$C_{n+1}=C_n\times (1+\dfrac{2,75}{100})=1,0275\times C_n$
Ainsi, $(C_n)$ est une suite géométrique de raison $1,0275$ et de premier terme $C_0=600$
donc pour tout entier $n, C_n=600\times 1,0275^n$
Le capital disponible au 1er janvier 2017 est : $$C_3=600\times1,0275^3\approx 650,87$$
Au 1er janvier 2017, Chloé n'aura pas une somme suffisante pour passer son permis.

Partie B

Chloé aura besoin de 1500 euros pour financer son permis. Ses parents lui conseillent de verser chaque mois sur le livret la somme supplémentaire de 25 euros, à partir du 1er février 2014. Ils lui expliquent que le taux annuel du livret jeune correspond à un taux mensuel de 0,226$\,\%$.

1. Ses parents lui présentent un extrait d'une page de tableur qui simule l'évolution d'épargne : $$\begin{array}{|c|c|} \hline &A& B\\ \hline 1 &01/01/2014 &600,00 \text{€}\\ \hline 2 &01/02/2014 &626,36 \text{€}\\ \hline 3 &01/03/2014 &652,77 \text{€}\\ \hline 4 &01/04/2014 &679,25 \text{€}\\ \hline 5 &01/05/2014 &705,78 \text{€}\\ \hline 6 &01/06/2014 &732,38 \text{€}\\ \hline 7 &... &...\\ \hline \end{array}$$
   1. Justifier que, dans la feuille de calcul ci-dessus, la formule à saisir dans la cellule $B2$ est 
      $=  1,00226 \times \text{B}1 + 25$
   Le coefficient multiplicateur associé à un pourcentage d'évolution de $0,226 \%$ est $1+\dfrac{0,226}{100}=1,00226$.
   
   La somme disponible chaque mois est obtenue en ajoutant 25 au produit de la somme disponible du mois précédent par 1,00226 donc la formule à saisir dans la cellule $B2$ est : $$=1,00226\times B1+25.$$
   2. Déterminer la somme qui serait disponible sur le livret au 1er juillet 2014.
   $732,38\times 1,00226 +25 \approx 759,04.$
   Au 1er juillet 2014, elle disposerait de 759,04 euros.
2. Chloé veut déterminer au bout de combien de mois elle aurait l'argent nécessaire pour financer son permis en suivant le conseil de ses parents. Elle décide de noter $u_{n}$ la somme, en euros, disponible le $n$-ième mois après l'ouverture du livret. Ainsi, $u_{0}$ vaut 600 euros.
   1. Exprimer $u_{n+1}$ en fonction de $u_{n}$.
   Pour tout entier naturel $n, u_{n+1}=1,00226\times u_n+25.$
   2. Chloé décide d'écrire l'algorithme suivant : Trois lignes de l'algorithme comportent des pointillés. Recopier ces lignes et les compléter pour que Chloé puisse déterminer le nombre de mois cherché.
   $$\begin{array}{|ll|}\hline\text{Variables}\\ \hspace{0,3cm}n :\text{ un nombre entier naturel}\\ \hspace{0,3cm}u : \text{ un nombre réel }\\\text{Initialisation}\\ \hspace{0,3cm}\text{ Affecter à } n \text{ la valeur } 0\\ \hspace{0,3cm}\text{ Affecter à } u \text{ la valeur } 600\\\text{Traitement}\\ \hspace{0,3cm} \text{ Tant que } u < 1500 \\ \hspace{0,6cm}\text{ Affecter à } n \text{ la valeur } n + 1 \\ \hspace{0,6cm}\text{ Affecter à } u \text{ la valeur }1,00226\times u+25\\ \hspace{0,3cm}\text{ Fin Tant que }\\\text{Sortie}\\ \hspace{0,3cm}\text{ Afficher }n\\ \hline \end{array}$$
   3. Au bout de combien de mois Chloé aura-t-elle l'argent nécessaire pour financer son permis si elle suit les conseils de ses parents ?
   On programme l'algorithme sur la calculatrice, on obtient en sortie 33.
   Chloé aura l'argent nécessaire pour financer son permis au bout de 33 mois.

Exercice 4 5 points

Probabilités

Une entreprise de transport dispose d'un nombre important de camions. On admet que la distance quotidienne parcourue par chaque camion, exprimée en kilomètres, peut être modélisée par une variable aléatoire $X$ qui suit la loi normale d'espérance $500$ et d'écart type $40$.

1. Donner la distance moyenne parcourue en un jour par un camion.
2. Déterminer la probabilité qu'un camion parcoure au moins $500$ km en un jour.
3. Déterminer la probabilité qu'un camion parcoure entre $380$ km et $460$ km en un jour.
4. Déterminer la probabilité qu'un camion parcoure plus de $460$ km en un jour.
5. Le directeur de l'entreprise affirme qu'environ 95$\,\%$ de ses camions parcourent entre $460$ et $540$ km par jour. A-t-il raison ?

Exercice 4 5 points

Probabilités

Une entreprise de transport dispose d'un nombre important de camions. On admet que la distance quotidienne parcourue par chaque camion, exprimée en kilomètres, peut être modélisée par une variable aléatoire $X$ qui suit la loi normale d'espérance $500$ et d'écart type $40$.

1. Donner la distance moyenne parcourue en un jour par un camion.
La distance quotidienne parcourue par chaque camion, est modélisée par une variable aléatoire X qui suit la loi normale d'espérance 500 donc :
La distance moyenne parcourue en un jour par un camion est de 500 km.
2. Déterminer la probabilité qu'un camion parcoure au moins $500$ km en un jour.
La variable aléatoire $X$ suit la loi normale d'espérance 500 donc $P(X\geq 500)=0,5$

La probabilité qu'un camion parcoure au moins 500 km en un jour est égale à 0,5.
3. Déterminer la probabilité qu'un camion parcoure entre $380$ km et $460$ km en un jour.

2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI

$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$

$$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$

 

La probabilité qu'un camion parcoure entre 380 km et 460 km en un jour est, arrondie au millième près, 0,157.
4. Déterminer la probabilité qu'un camion parcoure plus de $460$ km en un jour.

 

2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
Avec une calculatrice de type TI

$$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$

$$P( \5 \geq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
La probabilité qu'un camion parcoure plus de 460 km en un jour est, arrondie au millième près, 0,841.
5. Le directeur de l'entreprise affirme qu'environ 95$\,\%$ de ses camions parcourent entre $460$ et $540$ km par jour. A-t-il raison ?
Si $X$ suit la loi normale d'espérance $\mu$ et d'écart-type $\sigma$ alors $P(\mu-\sigma\leq X\leq \mu+\sigma)≈0,683$ d'où :

$P(460\leq X\leq 540)\approx 0,683$ par conséquent, le directeur a tort.