Baccalauréat STI2D et STL spécialité SPCLMétropole -- 7 septembre 2017 - Correction Exercice 1
Correction de l'exercice 1 (4 points)
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses est exacte. Aucune justification n'est demandée. Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point.Indiquer sur la copie le numéro de la question et la lettre correspondant à la réponse.
- On donne ci-dessous la courbe $\mathcal C$ représentative d'une fonction $f$ définie et dérivable sur $] 0~;~+\infty[$. On pose $I=\displaystyle\int_{1}^{2} f(x) d x$.
Un encadrement de $I$ est:
- $6<I<8$
- $1<I<2$
- $3<I<4$
- $13<I<16$
- La fonction $g$ est définie sur l'intervalle $] 0~;~+\infty[$ par $g(x)=(-2x+1) \ln(x) + 5$. La limite de cette fonction $g$ en $+\infty$ est égale à:
- $+\infty$
- $-\infty$
- $0$
- $5$
$\left.\begin{array}{l} \lim\limits_{x \to +\infty}~(-2x+1)=-\infty\\ \lim\limits_{x \to +\infty}~\ln x=+\infty\end{array}\right\} \quad \text{ Par produit } \lim\limits_{x \to +\infty}~(-2x+1)\ln x=-\infty$; puis en ajoutant 5 : $ \lim\limits_{x \to +\infty}~(-2x+1)\ln x+5=-\infty$ - La suite $(v_n)$ est géométrique de premier terme $v_0=4$ et de raison $q=0,5$.
La somme des 9 premiers termes de cette suite est égale à:- $4\times 0,5^8$
- $\dfrac{1-0,5^9}{1-0,5}$
- $8\times (1-0,5^9)$
- $6,9$
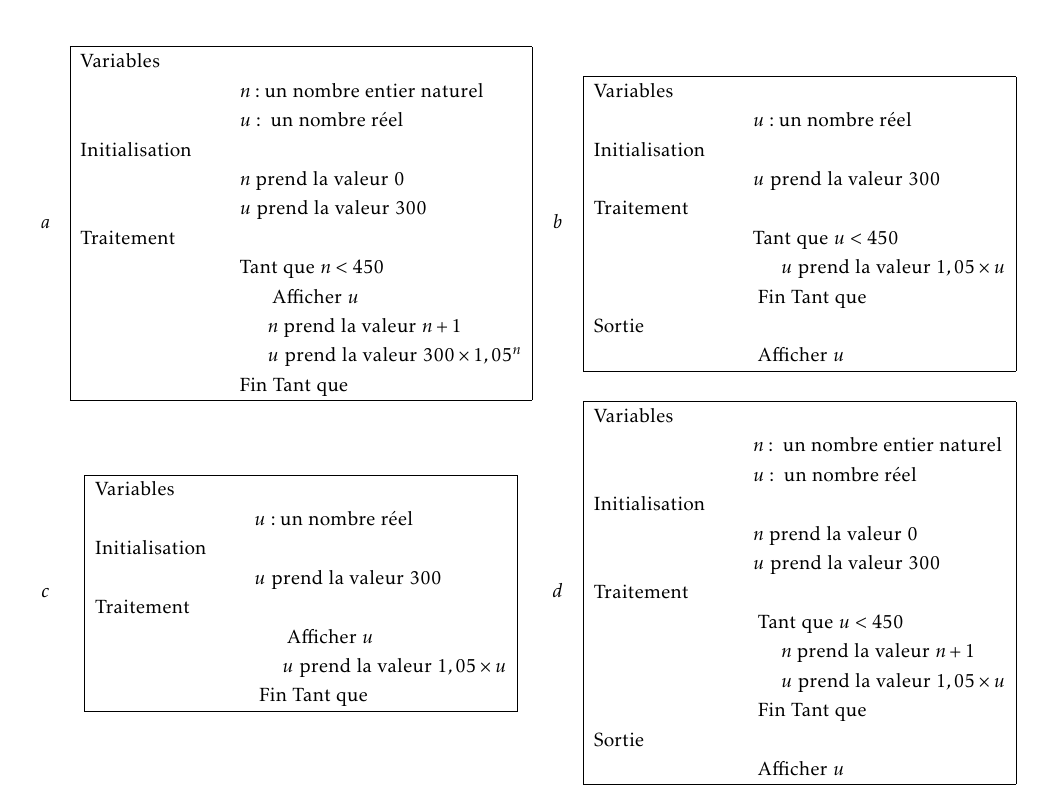
- La suite $(u_n)$ est la suite géométrique de premier terme $u_0=300$ et de raison $q=1,05$. L'algorithme qui calcule et affiche tous les termes strictement inférieurs à 450 de cette suite est:
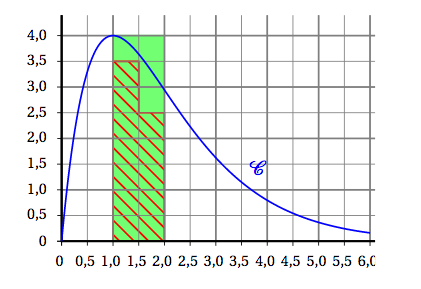
Sur l’intervalle $[1;2]$, la fonction $f$ est positive, donc l’intégrale $I=\displaystyle\int_{1}^{2} f(x) d x$ est égale à l’aire du domaine compris entre la courbe $C$, l’axe des abscisses, et les deux droites d’équations $x=1$et $x=2$. Le polygone intérieur au domaine hachuré en rouge a une aire de 3 qui est inférieure à $I$. Le polygone extérieur au domaine colorié en vert a une aire de 4 plus grande que $I$.
$ \lim\limits_{x \to +\infty}~g(x)=-\infty$
On utilise le résultat suivant : Somme $S$ de $N$ termes successifs si $q\neq1$ sinon $S=NP$:$$S = \dfrac{(1-q^{N})}{ 1-q}P$$ $$N =\text{ nombre de termes de la somme} $$ $$P = \text{premier terme de la somme }; $$ $$q =\text{ raison}$$ $(v_n)$ est une suite géométrique de premier terme $v_0=4$ et de raison $q=0,5$ donc la somme des 9 premiers termes de cette suite est égale à : $$\begin{array}{rl} S&=\dfrac{1-0,5^9}{1-0,5} \times 4\\ &=8\times\left( 1-0,5^9\right) \\ \end{array}$$
 La suite $(u_n)$ est la suite géométrique de premier terme $u_0=300$ et de raison $q=1,05$. L'algorithme qui calcule et affiche tous les termes strictement inférieurs à 450 de cette suite est:
La suite $(u_n)$ est la suite géométrique de premier terme $u_0=300$ et de raison $q=1,05$. L'algorithme qui calcule et affiche tous les termes strictement inférieurs à 450 de cette suite est:
L'algorithme a calcule et affiche les 450 premiers termes termes, il ne convient pas. Les algorithmes b et d n'affichent que le terme supérieur ou égal à 450. L'algorithme c est le seul qui calcule et affiche tous les termes strictement inférieurs à 450 de cette suite.
- Vues: 20906
