Baccalauréat STI2D et STL/SPCL - Polynésie juin 2019
Exercice 1 5 points
| Température extérieure T En plein hiver, en Europe, une maison est chauffée à 20 °C. La température extérieure est notée T . Dans tout l'exercice, on suppose que T < 20 . Température intérieure initiale 20 °C Lorsque le chauffage est coupé, la température intérieure diminue par perte de chaleur. |
 |
On modélise cette situation par une suite $\left(u_n\right)$ dont le terme général $u_n$ désigne la température intérieure de la maison $n$ heures après la coupure du chauffage. Pour une maison en maçonnerie traditionnelle et une température extérieure $T$ constante, on admet que, pour tout entier naturel $n$ : \[u_{n+1} = 0,99 u_n + \dfrac{T}{100}\quad \text{et} \quad u_0 = 20.\] Les parties A et B de cet exercice peuvent être traitées de manière indépendante.
Partie A
On suppose que la température extérieure $T$ est égale à 0° C. On a donc $T = 0$.
- Calculer les termes $u_1$ et $u_2$.
- Montrer que, dans ce cas, la suite $\left(u_n\right)$ est une suite géométrique dont on précisera le premier terme et la raison.
- Pour tout entier naturel $n$, exprimer $u_n$ en fonction de $n$.
- Déterminer la limite de la suite $\left(u_n\right)$. Justifier.
- Résoudre dans l'ensemble des entiers naturels l'inéquation $u_n < 5$.
- En déduire le nombre de jours à partir duquel la température intérieure est descendue en dessous de 5° C.
Partie B
On suppose que la température extérieure $T$ est égale à $-15$° C. On a donc $T = - 15$.
- Montrer que, dans ce cas, la suite $\left(u_n\right)$ est définie pour tout entier naturel $n$ par: \[u_{n+1} = 0,99 u_n - 0,15 \quad \text{et }\: u_0 = 20.\]
- Calculer les termes $u_1$ et $u_2$.
- Dans ce cas, la suite $\left(u_n\right)$ est-elle géométrique ? Justifier la réponse.
- On souhaite déterminer, à l'aide d'un algorithme, le nombre d'heures à partir duquel la température intérieure devient strictement inférieure à $5$° C. On utilise pour cela l'algorithme incomplet ci-contre dans lequel $U$ désigne un nombre réel et $N$ un nombre entier naturel. $$\begin{array}{|c|}\hline U \gets 20\\ N \gets 0\\ \text{Tant que} \ldots\\ \hspace{0.4cm} U \gets \ldots \\ \hspace{0.4cm} N \gets \ldots \\ \text{Fin Tant que} \\ \hline \end{array} $$
- Recopier et compléter l'algorithme.
- À l'aide de la calculatrice, déterminer le nombre d'heures recherché.
Correction de l'exercice 1 (5 points)
| Température extérieure T En plein hiver, en Europe, une maison est chauffée à 20 °C. La température extérieure est notée T . Dans tout l'exercice, on suppose que T < 20 . Température intérieure initiale 20 °C Lorsque le chauffage est coupé, la température intérieure diminue par perte de chaleur. |
 |
On modélise cette situation par une suite $\left(u_n\right)$ dont le terme général $u_n$ désigne la température intérieure de la maison $n$ heures après la coupure du chauffage. Pour une maison en maçonnerie traditionnelle et une température extérieure $T$ constante, on admet que, pour tout entier naturel $n$ : \[u_{n+1} = 0,99 u_n + \dfrac{T}{100}\quad \text{et} \quad u_0 = 20.\] Les parties A et B de cet exercice peuvent être traitées de manière indépendante.
Partie A
On suppose que la température extérieure $T$ est égale à 0° C. On a donc $T = 0$.
- Calculer les termes $u_1$ et $u_2$.
- $u_1=0,99\times u_0=0,99\times 20+\dfrac{0}{100}=19,8$
- $u_2=0,99\times u_1=0,99\times 19,8=19,602$
$$u_1=19,8 \text{ et } u_2=19,602$$
- Montrer que, dans ce cas, la suite $\left(u_n\right)$ est une suite géométrique dont on précisera le premier terme et la raison. pour tout entier naturel $n$ : \[u_{n+1} = 0,99 u_n + \dfrac{T}{100}=0,99u_n\quad \text{et} \quad u_0 = 20.\] La suite $\left(u_n\right)$ est donc une suite géométrique de raison 0,99 de premier terme $u_0=20$.
- Pour tout entier naturel $n$, exprimer $u_n$ en fonction de $n$. $u_n=q^n\times u_0=20\times 0,99^n$. $$u_n=20\times 0,99^n$$
- Déterminer la limite de la suite $\left(u_n\right)$. Justifier. Comme $0< 0,99< 1$; on déduit $\lim\limits_{n \to +\infty} 0,99^n= 0 $ puis $\lim\limits_{n \to +\infty}20\times 0,99^n= 0 $
- $$\text{Ainsi } \lim\limits_{n \to +\infty} u_n= 0 $$
- Résoudre dans l'ensemble des entiers naturels l'inéquation $u_n < 5$. $$\begin{array}{rll} u_n <5& \iff 20\times 0,99^n < 5&\\ & \iff 0,99^n <\frac{5}{20}&\\ &\iff 0,99^n < \frac{1}{4}&\\ &\iff \ln\left (0,99^n\right ) <\ln \left ( \frac{1}{4}\right )& \ln \text{est strictement croissante sur } ]0;+\infty[\\ &\iff n\ln\left (0,99 \right ) <\ln \left ( \frac{1}{4}\right )& \text{ car } \ln\left (a^n \right )=n\ln a\\ &\iff n> \dfrac{\ln \left ( \frac{1}{4}\right )}{\ln\left (0,99 \right )}&\text{ car } 0,99 <1 \text{ donc } \ln\left (0,99 \right ) <0\\ \end{array}$$ Grâce à une calculatrice, on obtient $\dfrac{\ln \left ( \frac{1}{4}\right )}{\ln\left (0,99 \right )}\approx 137,94$.
- Le vplus petit entier $n$ vérifiant $u_n < 5$ est $n=138$.
- Ainsi l'ensemble des solutions de l'inéquation $u_n < 5$ est l'ensemble des entiers naturels vérifiant $n\geq 138$.
- En déduire le nombre de jours à partir duquel la température intérieure est descendue en dessous de 5° C. $\dfrac{138}{24}=5,75$ donc la température passera en dessous de 5° C au bout de 6 jours.
Partie B
On suppose que la température extérieure $T$ est égale à $-15$° C. On a donc $T = - 15$.
- Montrer que, dans ce cas, la suite $\left(u_n\right)$ est définie pour tout entier naturel $n$ par: \[u_{n+1} = 0,99 u_n - 0,15 \quad \text{et }\: u_0 = 20.\] $$\begin{array}{rl} u_{n+1}&=0,99 u_n + \dfrac{T}{100}\quad \text{et} \quad u_0 = 20\\ &=0,99 u_n + \dfrac{15}{100}\quad \text{et} \quad u_0 = 20\\ &=0,99 u_n - 0,15 \quad \text{et }\: u_0 = 20 \end{array}$$
- Calculer les termes $u_1$ et $u_2$.
- $u_{1} = 0,99 u_0 - 0,15=0,99 \times 20-0,15=19,65$
- $u_{2} = 0,99 u_1 - 0,15=0,99 \times 19,65-0,15=19,3035$
- Dans ce cas, la suite $\left(u_n\right)$ est-elle géométrique ? Justifier la réponse. Si la suite $\left(u_n\right)$ était géométrique alors $\dfrac{u_2}{u_1}=\dfrac{u_1}{u_0}$;
- Or $\dfrac{u_2}{u_1}= \dfrac{19,3035}{19,65}\approx 0,9824$ et $\dfrac{u_1}{u_0}= \dfrac{19,65}{20}\approx 0,9825$.
- Donc la suite $\left(u_n\right)$ n'est pas géométrique.
- Calculer les termes $u_1$ et $u_2$.
- On souhaite déterminer, à l'aide d'un algorithme, le nombre d'heures à partir duquel la température intérieure devient strictement inférieure à $5$° C. On utilise pour cela l'algorithme incomplet ci-contre dans lequel $U$ désigne un nombre réel et $N$ un nombre entier naturel. $$\begin{array}{|c|}\hline U \gets 20\\ N \gets 0\\ \text{Tant que} \ldots\\ \hspace{0.4cm} U \gets \ldots \\ \hspace{0.4cm} N \gets \ldots \\ \text{Fin Tant que} \\ \hline \end{array} $$
- Recopier et compléter l'algorithme. $$\begin{array}{|c|}\hline U \gets 20\\ N \gets 0\\ \text{Tant que} U\>5\\ \hspace{0.4cm} U \gets 0,99U-0,15 \\ \hspace{0.4cm} N \gets N+1 \\ \text{Fin Tant que} \\ \hline \end{array} $$
- À l'aide de la calculatrice, déterminer le nombre d'heures recherché. A l'aide de la calculatrice, on obtient $u_{55}\approx 5,14$ et $u_{56}\approx 4,94$.
- Suivant ce modèle, la température intérieure devient strictement inférieure à $5$° C au bout de 56 heures , soit 4 jours et 8 heures.
Exercice 2 6 points
Les parties A et B de cet exercice peuvent être traitées de manière indépendante.
Partie A
On considère la fonction $f$ définie sur $[0~;~4[$ par: \[f(x) = 10x + \ln( 4 - x) - \ln 4.\] On note $\mathcal{C}_f$ sa courbe représentative dans un repère.
- Calculer $f(0)$.
- Déterminer $\displaystyle\lim_{x \to 4}f(x)$.
- En déduire que la courbe $\mathcal{C}_f$ admet une asymptote dont on précisera une équation.
- On appelle $f'$ la fonction dérivée de $f$ sur l'intervalle $[0~;~4[$. Montrer que, pour tout $x$ appartenant à l'intervalle $[0~;~4[$, on a: $f'(x) = \dfrac{39 - 10x}{4 - x}$.
- Étudier le signe de $f'(x)$ pour tout $x$ appartenant à l'intervalle $[0~;~4[$.
- Justifier que la fonction $f$ atteint un maximum en 3,9. Donner une valeur approchée au dixième de ce maximum.
Partie B
Un constructeur de voitures électriques affirme que ses modèles peuvent atteindre la vitesse de $100$ km.h$^{-1}$ en moins de $3$ secondes. Pour vérifier cette affirmation, des journalistes ont testé une de ces voitures en réalisant l'essai suivant :
- dans un premier temps, augmentation de la vitesse de 0 à $35,3$ m.s$^{-1}$ (soit environ $127$ km.h$^{-1}$) en $3,9$ s ;
- dans un deuxième temps, stabilisation de la vitesse à $35,3$ m.s$^{-1}$.
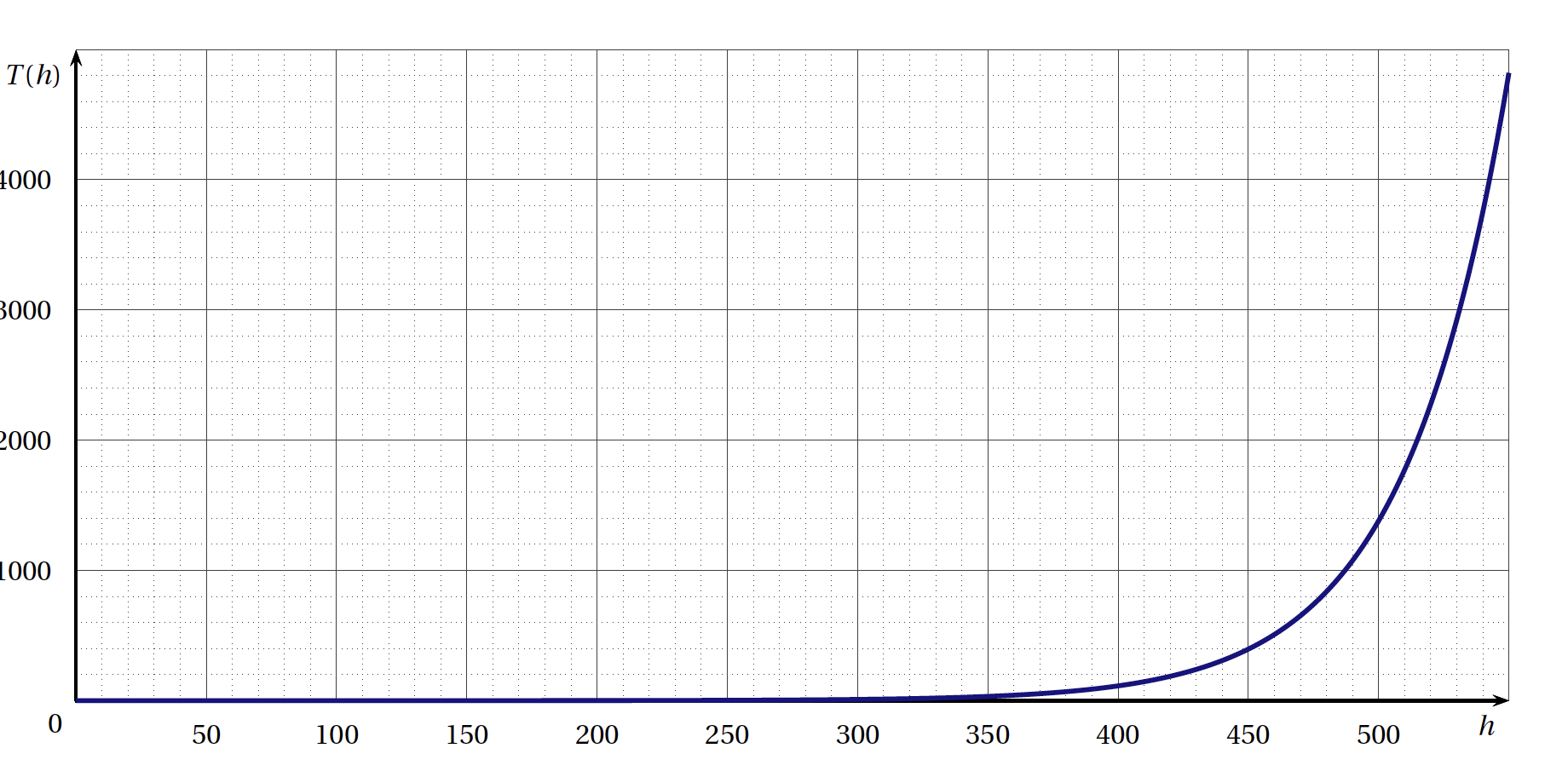
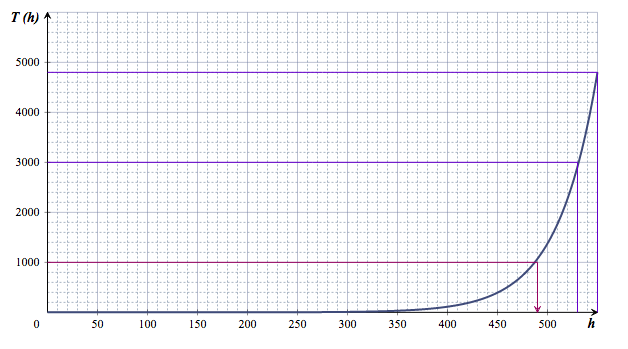
L'évolution de la vitesse en fonction du temps est représentée par le graphique ci-dessous: 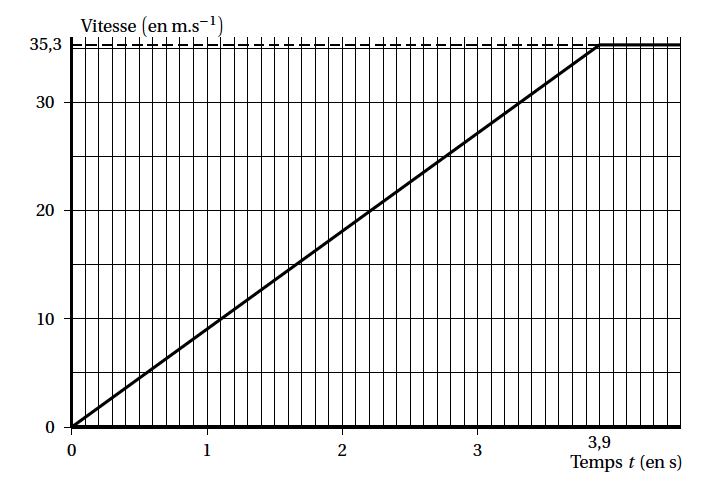
Durant la phase d'accélération, la vitesse de la voiture est modélisée par la fonction $f$ étudiée dans la partie A et définie par : \[f(t) = 10t + \ln(4 - t) - \ln 4 \quad \text{avec }\:t \in [0~;~3,9]\] où $t$ est exprimé en seconde et $f(t)$ est exprimée en m.s$^{-1}$.
- Calculer $f(3)$.
- L'affirmation du constructeur est-elle vérifiée ?
- La distance $D$, exprimée en mètre, parcourue durant la phase d'accélération est donnée par la formule : $D = \displaystyle\int_0^{3,9} f(t)\: \text{d}t$.
- On considère la fonction $F$ définie sur $[0~;~3,9]$ par: \[F(t) = 5 t^2 - t + (t - 4)\left [\ln ( 4 - t) - \ln 4 \right].\] Montrer que la fonction $F$ est une primitive de $f$.
- Calculer la distance $D$ arrondie au dixième.
Correction de l'exercice 2 (6 points)
Les parties A et B de cet exercice peuvent être traitées de manière indépendante.
Partie A
On considère la fonction $f$ définie sur $[0~;~4[$ par: \[f(x) = 10x + \ln( 4 - x) - \ln 4.\] On note $\mathcal{C}_f$ sa courbe représentative dans un repère.
- Calculer $f(0)$. $f(0) = 10\times 0 + \ln( 4 ) - \ln 4=0$
- $f(0)=0$.
- Déterminer $\displaystyle\lim_{x \to 4}f(x)$. $\left.\begin{array}{l} \lim\limits_{x \to 4^-}~(4-x)=0^+ \\ \lim\limits_{t \to 0^+}~ \ln t=-\infty \end{array}\right\}\; \text{ par composée }\lim\limits_{x \to 4^-}~ \ln(4-x)=-\infty $
- $$\left.\begin{array}{l} \lim\limits_{x \to 4^-}~10x=40\\ \lim\limits_{x \to 4^-}~\ln(4-x)=-\infty\\ \lim\limits_{x \to 4^-}~-\ln 4= -\ln 4\end{array}\right\} \quad \text{ Par somme } \lim\limits_{x \to 4^-}~f(x)=-\infty$$
- En déduire que la courbe $\mathcal{C}_f$ admet une asymptote dont on précisera une équation. $\displaystyle\lim_{x\rightarrow 4^-}f(x)=-\infty$, donc la droite d'équation $x=4$ est asymptote verticale à $\mathcal{C}_f$.
- On appelle $f'$ la fonction dérivée de $f$ sur l'intervalle $[0~;~4[$. Montrer que, pour tout $x$ appartenant à l'intervalle $[0~;~4[$, on a: $f'(x) = \dfrac{39 - 10x}{4 - x}$. \[f(x) = 10x + \ln( 4 - x) - \ln 4.\] donc $$\begin{array}{rll} f'(x)&=10+\dfrac{-1}{4-x} &\text{ car } \left (\ln u\right )'= \dfrac{u'}{u}\\ &&\\ & =10+\dfrac{1}{x-4}&\\ &&\\ &=\dfrac{10(x-4)}{x-4}+\dfrac{1}{x-4}&\\ &&\\ &=\dfrac{10x-40+1}{x-4}&\\ &&\\ &=\dfrac{10x-39}{x-4}&\\ &&\\ &= \dfrac{39 - 10x}{4 - x}&\\ \end{array}$$ Ainsi, pour tout $x$ appartenant à l'intervalle $[0~;~4[$, on a: $f'(x) = \dfrac{39 - 10x}{4 - x}$.
- Étudier le signe de $f'(x)$ pour tout $x$ appartenant à l'intervalle $[0~;~4[$. Pour tout $x$ appartenant à l'intervalle $[0~;~4[$, on a $4-x>0$, donc $f'(x)$ a le signe de $39-10x$. $$\begin{array}{llcrl} f'(x)=0&\iff 39-10x=0 &&f'(x) >0&\iff 39-10x>0\\ & \iff 10x=39&&&\iff 39 >10x\\ &\iff x=\dfrac{39}{10}&&&\iff x< \dfrac{39}{10} \end{array}$$
- Justifier que la fonction $f$ atteint un maximum en 3,9. Donner une valeur approchée au dixième de ce maximum. On déduit le tableau de variation de $f$ sur l'intervalle $[0~;~4[$.
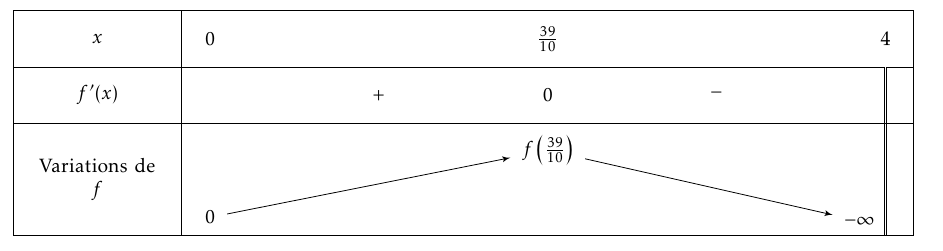
- la fonction $f$ atteint ainsi un maximum en $\dfrac{39}{10}=3,9$ qui vaut $f(3,9)$ $$\begin{array}{rl} f(3,9) &= 10\times 3,9 + \ln( 4 - 3,9) - \ln 4 \\ & =39+\ln(0,1)-\ln 4\\ &=39-\ln\left (40\right )\\ &\approx 35,3 \end{array}$$ La fonction $f$ atteint un maximum en 3,9 qui vaut $f(3,9)\approx 35,3$.
Partie B
Un constructeur de voitures électriques affirme que ses modèles peuvent atteindre la vitesse de $100$ km.h$^{-1}$ en moins de $3$ secondes. Pour vérifier cette affirmation, des journalistes ont testé une de ces voitures en réalisant l'essai suivant :
- dans un premier temps, augmentation de la vitesse de 0 à $35,3$ m.s$^{-1}$ (soit environ $127$ km.h$^{-1}$) en $3,9$ s ;
- dans un deuxième temps, stabilisation de la vitesse à $35,3$ m.s$^{-1}$.
L'évolution de la vitesse en fonction du temps est représentée par le graphique ci-dessous: 
Durant la phase d'accélération, la vitesse de la voiture est modélisée par la fonction $f$ étudiée dans la partie A et définie par : \[f(t) = 10t + \ln(4 - t) - \ln 4 \quad \text{avec }\:t \in [0~;~3,9]\] où $t$ est exprimé en seconde et $f(t)$ est exprimée en m.s$^{-1}$.
- Calculer $f(3)$. $$f(3) = 10\times 3 + \ln(1) - \ln 4=30-\ln 4$$
- L'affirmation du constructeur est-elle vérifiée ? Au bout de 3 secondes la vitesse est donc $(30-\ln 4)$m.s$^{-1}$, (soit environ $(30-\ln 4)\times 3600\times 10^{-3}\approx 103$ km.h$^{-1}$).
- L'affirmation du constructeur est donc vérifiée.
- La distance $D$, exprimée en mètre, parcourue durant la phase d'accélération est donnée par la formule : $D = \displaystyle\int_0^{3,9} f(t)\: \text{d}t$.
- On considère la fonction $F$ définie sur $[0~;~3,9]$ par: \[F(t) = 5 t^2 - t + (t - 4)\left [\ln ( 4 - t) - \ln 4 \right].\] Montrer que la fonction $F$ est une primitive de $f$. $F$ est une primitive de $f$ ssi $F'=f$
- $$\begin{array}{rll} F'(t)&= 5\times 2t -1+ 1\times \left [\ln ( 4 - t) - \ln 4 \right] +(t-4)\times \dfrac{-1}{4-t} & \text{ car } (uv)'=u'v+v'u\\ & =10t -1+ \ln ( 4 - t) - \ln 4+1&\\ &=10t + \ln ( 4 - t) -\ln 4&\\ &=f(t) \end{array}$$ Ainsi $F$ est une primitive de $f$ .
- Calculer la distance $D$ arrondie au dixième. $$\begin{array}{rl|crl} D &= \displaystyle\int_0^{3,9} f(t)\: \text{d}t &&&\\ &=\left [F(t)\right ] _0^{3,9}&&&\\ &=F(3,9)-F(0)&&&\\ F(3,9)&=5 \times 3,9^2 -3,9 + (3,9 - 4)\left [\ln ( 4 - 3,9) - \ln 4 \right] &F(0)&= 5 \times 0^2 - 0 + (0 - 4)\left [\ln 4 - \ln 4 \right]. \\ &=72,15-0,1\times \left (\ln ( 0,1) - \ln 4\right )&&=0\\ & =72,15+0,1\ln(40)&&\\ \end{array}$$ $$D=72,15+0,1\ln(40)\approx 72,5$$
Exercice 3 5 points
Les résistances et les condensateurs sont des composants électroniques utilisés dans le domaine du son pour concevoir des filtres. Placé en sortie d'un microphone, un filtre atténue plus ou moins les sons selon leur fréquence $f$, exprimée en Hertz (Hz). 
Pour un filtre donné, l'atténuation d'un son se calcule à l'aide de deux nombres complexes $z_R$.
Dans tout l'exercice, on suppose que $z_R = 10$ et $z_C = - \dfrac{1000\sqrt{3}}{f}\text{i}$ , où i désigne le nombre complexe de module 1 et d'argument $\dfrac{\pi}{2}$..
Les parties A et B peuvent être traitées de manière indépendante.
Partie A : Effet du filtre sur un son grave
On choisit un son grave de fréquence $f = 100$.
- Montrer que $z_C = - 10\sqrt{3} \text{i}$.
- Déterminer la forme exponentielle de $z_C$.
- On considère le nombre complexe $Z = z_R + z_C$. On a donc $Z = 10 - 10\sqrt{3} \text{i}$. Déterminer la forme exponentielle de $Z$ .
- On considère le nombre complexe $z_G$ défini par : $z_G = \dfrac{z_C}{z_R + z_C}$. Montrer que $z_G = \dfrac{\sqrt{3}}{2}\text{e}^{- \text{i}\frac{\pi}{6}}$.
- Le module du nombre complexe $z_G$ est appelé gain du filtre. Donner la valeur exacte du gain du filtre puis une valeur approchée au centième.
Partie B : Effet du filtre sur un son aigu
On choisit un son aigu de fréquence $f = 1000 \sqrt{3}$.
- Montrer que le nombre complexe $z_G$ défini par $z_G = \dfrac{z_C}{z_R + z_C}$ est égal à $\dfrac{- \text{i}}{10 - \text{i}}$.
- Déterminer la forme algébrique de $z_G$ .
- Calculer la valeur exacte du gain du filtre $\left|z_G\right|$ et en donner une valeur approchée au centième.
Correction de l'exercice 3 (5 points)
Les résistances et les condensateurs sont des composants électroniques utilisés dans le domaine du son pour concevoir des filtres. Placé en sortie d'un microphone, un filtre atténue plus ou moins les sons selon leur fréquence $f$, exprimée en Hertz (Hz). 
Pour un filtre donné, l'atténuation d'un son se calcule à l'aide de deux nombres complexes $z_R$.
Dans tout l'exercice, on suppose que $z_R = 10$ et $z_C = - \dfrac{1000\sqrt{3}}{f}\text{i}$ , où i désigne le nombre complexe de module 1 et d'argument $\dfrac{\pi}{2}$..
Les parties A et B peuvent être traitées de manière indépendante.
Partie A : Effet du filtre sur un son grave
On choisit un son grave de fréquence $f = 100$.
- Montrer que $z_C = - 10\sqrt{3} \text{i}$. Si $f = 100$ alors $z_C =- \dfrac{1000\sqrt{3}}{f}\text{i}=- \dfrac{1000\sqrt{3}}{100}\text{i}= - 10\sqrt{3} \text{i}$.
- On a donc bien $z_C = - 10\sqrt{3} \text{i}$.
- Déterminer la forme exponentielle de $z_C$. On a $z_C = - 10\sqrt{3} \text{i}= 10\sqrt 3\times (-\text{i})= 10\sqrt3 \text{e}^{-\text{i}\frac{\pi}{2}} $
- On considère le nombre complexe $Z = z_R + z_C$. On a donc $Z = 10 - 10\sqrt{3} \text{i}$. Déterminer la forme exponentielle de $Z$ . $Z = 10 - 10\sqrt{3} \text{i}$ $$\begin{array}{cc} \text{Module} & \text{Argument} \\ \begin{array}{rl|rl} |Z |&=\sqrt{a^2+b^2} \\ & =\sqrt{ 10^2+\left (10\sqrt{3}\right )^2}\\ &=\sqrt {100+300}\\ &= 20 \end{array}& \left\lbrace \begin{array}{l} \cos \theta=\frac{a}{r}~=\frac{10}{20}=\frac{1}{2}\\ ~\sin \theta=\frac{b}{r}~=-\frac{10\sqrt 3}{20}=-\frac{\sqrt 3}{2} \end{array} \right.\\ &\text{ Donc } \theta = -\frac{\pi}{3} \text{ convient } \end{array}$$ $$Z= 10 - 10\sqrt{3} \text{i}= 20\left(\cos\left(-\frac{\pi}{3} \right) +\text{i}\sin \left(-\frac{\pi}{3} \right) \right) = 20 \text{e}^{-\text{i}\frac{\pi}{3}} $$
- On considère le nombre complexe $z_G$ défini par : $z_G = \dfrac{z_C}{z_R + z_C}$. Montrer que $z_G = \dfrac{\sqrt{3}}{2}\text{e}^{- \text{i}\frac{\pi}{6}}$. $$\begin{array}{rl} z_G& = \dfrac{z_C}{z_R + z_C} \\ &\\ &= \dfrac{z_C}{z_G}\\ &\\ & =\dfrac{10\sqrt3 \text{e}^{-\text{i}\frac{\pi}{2}}}{ 20 \text{e}^{-\text{i}\frac{\pi}{3}}} \\ &\\ & = \dfrac{\sqrt{3}}{2} \text{e}^{-\text{i}\frac{\pi}{2}+\text{i}\frac{\pi}{3}} \\ &\\ &=\dfrac{\sqrt{3}}{2}\text{e}^{- \text{i}\frac{\pi}{6}} \end{array}$$
- Le module du nombre complexe $z_G$ est appelé gain du filtre. Donner la valeur exacte du gain du filtre puis une valeur approchée au centième. $$ |Z_G |=\dfrac{\sqrt{3}}{2} \approx 0,87$$. Le gain du filtre vaut 0,87 au centième près.
Partie B : Effet du filtre sur un son aigu
On choisit un son aigu de fréquence $f = 1000 \sqrt{3}$.
- Montrer que le nombre complexe $z_G$ défini par $z_G = \dfrac{z_C}{z_R + z_C}$ est égal à $\dfrac{- \text{i}}{10 - \text{i}}$. $$\begin{array}{rl} z_C&= - \dfrac{1000\sqrt{3}}{1000 \sqrt{3}}\text{i}\\ & = -\text{i} \\ \text{ Alors }z_G &= \dfrac{z_C}{z_R + z_C} \\ &=\dfrac{- \text{i}}{10 - \text{i}} \end{array}$$
- Déterminer la forme algébrique de $z_G$ . $$\begin{array}{rl} z_G& =\dfrac{- \text{i}}{10 - \text{i}}\\ & =\dfrac{- \text{i}\times \left ( 10 + \text{i}\right )}{\left (10 - \text{i}\right )\times \left ( 10 + \text{i}\right )}\\ & =\dfrac{ 1-10 \text{i}}{\left (10 ^2+1^2\right )}\\ & =\dfrac{ 1}{101}-\dfrac{ 10}{101} \text{i}\\ \end{array}$$ $$z_G=\dfrac{ 1}{101}-\dfrac{ 10}{101} \text{i}$$
- Calculer la valeur exacte du gain du filtre $\left|z_G\right|$ et en donner une valeur approchée au centième. $$\begin{array}{rl} \rvert z_G\rvert & =\left \rvert \dfrac{- \text{i}}{10 - \text{i}}\right \rvert \\ & =\dfrac{ \rvert - \text{i} \rvert }{ \rvert10 - \text{i} \rvert } \\ &=\dfrac{1}{\sqrt{1^2+10^2}}\\ &=\dfrac{1}{\sqrt{101}}\\ &\approx 0,10 \end{array}$$
Exercice 4 5 points
Cet exercice est composé de quatre affirmations indépendantes. Pour chacune d'entre elles, préciser si elle est juste ou fausse. Les réponses doivent être justifiées. Une réponse non justifiée ne rapporte aucun point.
Une nouvelle gamme de téléphones portables est à l'étude.
- La durée de fonctionnement, exprimée en jour, du processeur de ce téléphone portable est modélisée par une variable aléatoire $X$ qui suit la loi exponentielle dont l'espérance est égale à $1~0000$ jours. La durée de garantie légale du téléphone portable est de $2$ ans, soit $730~$jours.
AFFIRMATION 1 : La probabilité que le processeur s'arrête de fonctionner durant la période de garantie est égale à $\text{e}^{-0.073}$. - Pour anticiper la charge de travail du service après-vente, des tests ont été effectués en vue d'estimer le temps de réparation d'un téléphone sous garantie. Ce temps, exprimé en minute, peut être modélisé par une variable aléatoire $T$ qui suit la loi normale d'espérance $\mu = 50$ et d'écart-type $\sigma = 7$.
AFFIRMATION 2 : La probabilité, arrondie au millième, que le temps de réparation T soit inférieur à 1 heure est $0,923$. - Une amélioration technique a été apportée. Désormais, la probabilité qu'un téléphone soit réparable en moins d'une heure est estimée à $p = 0,97$. Un atelier du service après-vente prévoit de réparer $200$ téléphones portables. On s'intéresse aux échantillons constitués, aléatoirement, de $200$ téléphones portables à réparer.
AFFIRMATION 3 : Pour de tels échantillons, en arrondissant les bornes au millième, l'intervalle de fluctuation asymptotique au seuil de 95 % de la proportion de téléphones réparables en moins d'une heure est $[0,946~;~ 0,994]$. - Un fabricant de processeurs pour téléphone portable certifie que, dans son stock, la probabilité qu'un processeur neuf soit défectueux est $p = 0,0001 $. On désigne par $Y$ la variable aléatoire correspondant au nombre de processeurs défectueux dans un lot de $200$ prélevés au hasard. Le stock est suffisamment important pour assimiler ce prélèvement à un tirage avec remise. Ainsi, la variable aléatoire $Y$ suit la loi binomiale de paramètres $n = 200$ et $p = 0,0001 $.
AFFIRMATION 4 : La probabilité, arrondie au millième, qu'il n'y ait aucun processeur défectueux dans un lot de $200$ processeurs est égale à $0,980$.
Exercice 4 5 points
Cet exercice est composé de quatre affirmations indépendantes. Pour chacune d'entre elles, préciser si elle est juste ou fausse. Les réponses doivent être justifiées. Une réponse non justifiée ne rapporte aucun point.
Une nouvelle gamme de téléphones portables est à l'étude.
- La durée de fonctionnement, exprimée en jour, du processeur de ce téléphone portable est modélisée par une variable aléatoire $X$ qui suit la loi exponentielle dont l'espérance est égale à $1~0000$ jours. La durée de garantie légale du téléphone portable est de $2$ ans, soit $730~$jours.
AFFIRMATION 1 : La probabilité que le processeur s'arrête de fonctionner durant la période de garantie est égale à $\text{e}^{-0.073}$.
De $E(X)=1000$, on déduit $\dfrac{1}{\lambda}=10000$, soit $\lambda = 10^{-4}$.
- On veut calcler $P(T\leq 730)$. $$\begin{array}{rl} P(X\leq t)&= \displaystyle\int_0^t \lambda\text{e}^{-\lambda .x} \; \text{d} x\\ &=\left [ -\text{e}^{-\lambda .x} \right ] _0^t\\ &=-\text{e}^{-\lambda \times 0} - \text{e}^{-\lambda .t} \\ &=1--\text{e}^{-\lambda .t} \end{array}$$ Alors $P(X\leq 730)=1- \text{e}^{-10^{-4} \times 730}=1- \text{e}^{-0,073}$.
L'affirmation 1 est donc fausse.
- Pour anticiper la charge de travail du service après-vente, des tests ont été effectués en vue d'estimer le temps de réparation d'un téléphone sous garantie. Ce temps, exprimé en minute, peut être modélisé par une variable aléatoire $T$ qui suit la loi normale d'espérance $\mu = 50$ et d'écart-type $\sigma = 7$.
AFFIRMATION 2 : La probabilité, arrondie au millième, que le temps de réparation T soit inférieur à 1 heure est $0,923$.
On calcule $P(T\leq 60)$:
2ND DISTR 2NORMALFRép( -10^(99) , \1,$\2$,$\3$)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(-10^{99},\1,\2,\3) \approx \4$$
L'affirmation 2 est donc vraie.
- Une amélioration technique a été apportée. Désormais, la probabilité qu'un téléphone soit réparable en moins d'une heure est estimée à $p = 0,97$. Un atelier du service après-vente prévoit de réparer $200$ téléphones portables. On s'intéresse aux échantillons constitués, aléatoirement, de $200$ téléphones portables à réparer.
AFFIRMATION 3 : Pour de tels échantillons, en arrondissant les bornes au millième, l'intervalle de fluctuation asymptotique au seuil de 95 % de la proportion de téléphones réparables en moins d'une heure est $[0,946~;~ 0,994]$.
La proportion $p$ est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times p $=\3 et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique ne sont pas sont réunies !
L'intervalle de fluctuation asymptotique au seuil de $95\% $ est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$
L'affirmation 3 est donc vraie.
- Un fabricant de processeurs pour téléphone portable certifie que, dans son stock, la probabilité qu'un processeur neuf soit défectueux est $p = 0,0001 $. On désigne par $Y$ la variable aléatoire correspondant au nombre de processeurs défectueux dans un lot de $200$ prélevés au hasard. Le stock est suffisamment important pour assimiler ce prélèvement à un tirage avec remise. Ainsi, la variable aléatoire $Y$ suit la loi binomiale de paramètres $n = 200$ et $p = 0,0001 $.
AFFIRMATION 4 : La probabilité, arrondie au millième, qu'il n'y ait aucun processeur défectueux dans un lot de $200$ processeurs est égale à $0,980$.
On calcule $P(Y=0)$.
2ND DISTR 0binomFdP( \1 , \2,\3)EXE
Avec une calculatrice de type TI $binomFdP(\1,\2,\3) \approx \4$
L'affirmation 4 est donc vraie.
- Vues: 22785