Baccalauréat STI2D et STL/SPCL - Polynésie juin 2019 - Exercice 2

Page 3 sur 8: Exercice 2

Exercice 2 6 points

Fonctions

Les parties A et B de cet exercice peuvent être traitées de manière indépendante.

Partie A

On considère la fonction $f$ définie sur $[0~;~4[$ par: $$f(x) = 10x + \ln( 4 - x) - \ln 4.$$ On note $\mathcal{C}_f$ sa courbe représentative dans un repère.

1. Calculer $f(0)$.
2. 1. Déterminer $\displaystyle\lim_{x \to 4}f(x)$.
   2. En déduire que la courbe $\mathcal{C}_f$ admet une asymptote dont on précisera une équation.
3. 1. On appelle $f'$ la fonction dérivée de $f$ sur l'intervalle $[0~;~4[$. Montrer que, pour tout $x$ appartenant à l'intervalle $[0~;~4[$, on a: $f'(x) = \dfrac{39 - 10x}{4 - x}$.
   2. Étudier le signe de $f'(x)$ pour tout $x$ appartenant à l'intervalle $[0~;~4[$.
   3. Justifier que la fonction $f$ atteint un maximum en 3,9. Donner une valeur approchée au dixième de ce maximum.

 

Partie B

Un constructeur de voitures électriques affirme que ses modèles peuvent atteindre la vitesse de $100$ km.h$^{-1}$ en moins de $3$ secondes. Pour vérifier cette affirmation, des journalistes ont testé une de ces voitures en réalisant l'essai suivant :

• dans un premier temps, augmentation de la vitesse de 0 à $35,3$ m.s$^{-1}$ (soit environ $127$ km.h$^{-1}$) en $3,9$ s ;
• dans un deuxième temps, stabilisation de la vitesse à $35,3$ m.s$^{-1}$.

L'évolution de la vitesse en fonction du temps est représentée par le graphique ci-dessous: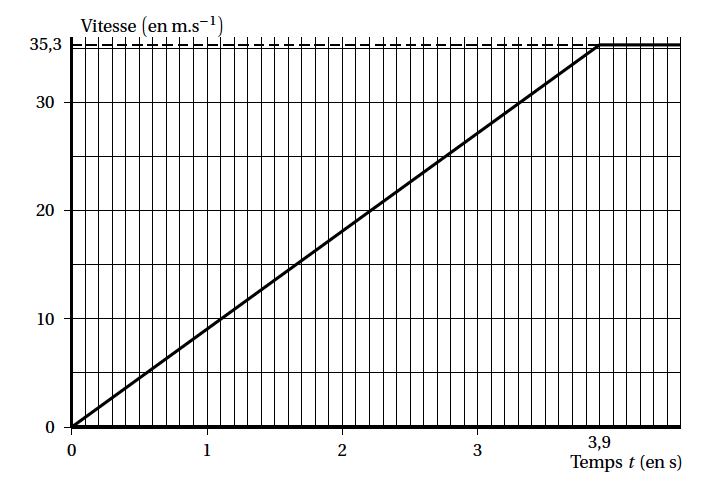

Durant la phase d'accélération, la vitesse de la voiture est modélisée par la fonction $f$ étudiée dans la partie A et définie par : $$f(t) = 10t + \ln(4 - t) - \ln 4 \quad \text{avec }\:t \in [0~;~3,9]$$ où $t$ est exprimé en seconde et $f(t)$ est exprimée en m.s$^{-1}$.

1. 1. Calculer $f(3)$.
   2. L'affirmation du constructeur est-elle vérifiée ?
2. La distance $D$, exprimée en mètre, parcourue durant la phase d'accélération est donnée par la formule : $D = \displaystyle\int_0^{3,9} f(t)\: \text{d}t$.
   1. On considère la fonction $F$ définie sur $[0~;~3,9]$ par: $$F(t) = 5 t^2 - t + (t - 4)\left [\ln ( 4 - t) - \ln 4 \right].$$ Montrer que la fonction $F$ est une primitive de $f$.
   2. Calculer la distance $D$ arrondie au dixième.