Baccalauréat S Amérique du Nord 2 juin 2017 - Exercice 4

Page 7 sur 10: Exercice 4

Exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Un particulier s'intéresse à l'ombre portée sur sa future véranda par le toit de sa maison quand le soleil est au zénith. Cette véranda est schématisée ci-dessous en perspective cavalière dans un repère orthonormé $\left(\text{O},\vec{\imath},\vec{\jmath},\vec{k}\right)$. Le toit de la véranda est constitué de deux faces triangulaires SEF et SFG.

• Les plans (SOA) et (SOC) sont perpendiculaires.
• Les plans (SOC) et (EAB) sont parallèles, de même que les plans (SOA) et (GCB).
• Les arêtes [UV) et [EF] des toits sont parallèles.

Le point K appartient au segment [SE], le plan (UVK) sépare la véranda en deux zones, l'une éclairée et l'autre ombragée. Le plan (UVK) coupe la véranda selon la ligne polygonale KMNP qui est la limite ombre-soleil.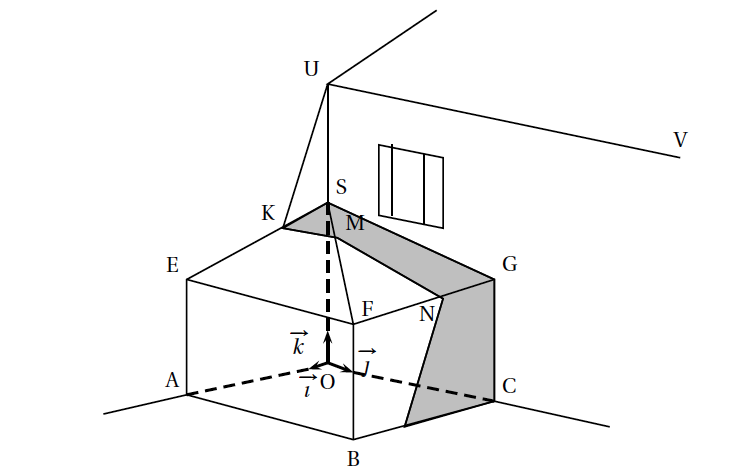

1. Sans calcul, justifier que :
   1. le segment [KM] est parallèle au segment [UV] ;
   2. le segment [NP] est parallèle au segment [UK].
2. Dans la suite de l'exercice, on se place dans le repère orthonormé $\left(\text{O},\vec{\imath},\vec{\jmath},\vec{k}\right)$. Les coordonnées des différents points sont les suivantes : A(4;0;0), B(4;5;0), C(0;5;0), E(4;0;2, 5), F(4;5;2,5), G(0;5;2,5), S(0;0;3,5), U(0;0;6) et V(0;8;6). On souhaite déterminer de façon exacte la section des faces visibles de la véranda par le plan (UV K) qui sépare les zones ombragée et ensoleillée.
   1. Au moment le plus ensoleillé, le point K a pour abscisse $1,2$. Vérifier que les coordonnées du point K sont (1,2;0;3,2).
   2. Montrer que le vecteur $ \vec{n}$ de coordonnées (7;0;3) est un vecteur normal au plan (UVK) et en déduire une équation cartésienne du plan (UVK).
   3. Déterminer les coordonnées du point N intersection du plan (UVK) avec la droite (FG).
   4. Expliquer comment construire la ligne polygonale sur le schéma de la véranda.
3. Afin de faciliter l'écoulement des eaux de pluie, l'angle du segment [SG] avec l'horizontale doit être supérieur à 7 °. Cette condition est-elle remplie ?