Baccalauréat S Amérique du Nord 2 juin 2017 - Correction Exercice 4

Page 8 sur 10: Correction Exercice 4

Correction de l'exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Un particulier s'intéresse à l'ombre portée sur sa future véranda par le toit de sa maison quand le soleil est au zénith. Cette véranda est schématisée ci-dessous en perspective cavalière dans un repère orthonormé $\left(\text{O},\vec{\imath},\vec{\jmath},\vec{k}\right)$. Le toit de la véranda est constitué de deux faces triangulaires SEF et SFG.

• Les plans (SOA) et (SOC) sont perpendiculaires.
• Les plans (SOC) et (EAB) sont parallèles, de même que les plans (SOA) et (GCB).
• Les arêtes [UV) et [EF] des toits sont parallèles.

Le point K appartient au segment [SE], le plan (UVK) sépare la véranda en deux zones, l'une éclairée et l'autre ombragée. Le plan (UVK) coupe la véranda selon la ligne polygonale KMNP qui est la limite ombre-soleil.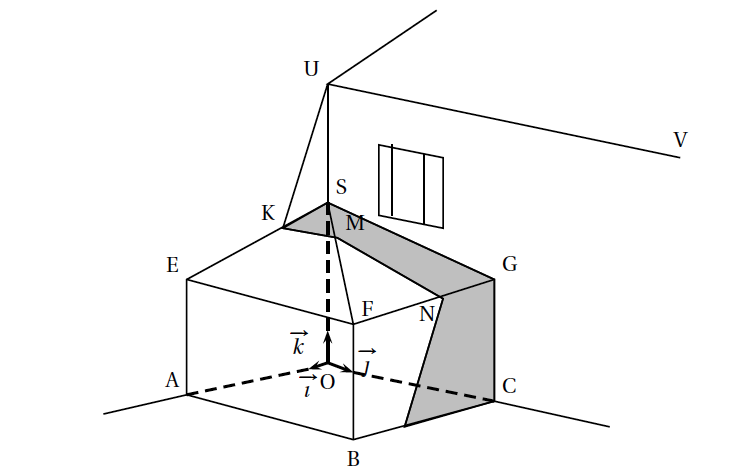

1. Sans calcul, justifier que :
   1. le segment [KM] est parallèle au segment [UV] ;
   La droite $(UV)$ du plan $(UVK)$ et la droite $(EF)$ du plan $(SEF)$ sont parallèles.
   Les plans $(UVK)$ et $(SEF)$ sont sécants selon la droite $(KM)$.
   D’après le théorème du toit les droites $(KM)$, $(UV)$ et $(EF)$ sont parallèles.
   $\quad$
   
   2. le segment [NP] est parallèle au segment [UK].
   Les plans $(SEA)$ et $(GCB)$ sont parallèles.
   Le plan $(UKV)$ coupe le plan $(SEA)$ selon la droite $(UK)$.
   Par conséquent le plan $(UKV)$ coupe le plan $(GCB)$ selon une droite qui parallèle à $(UK)$.
   Ainsi $(UK)$ et $(NP)$ sont parallèles.
   $\quad$
2. Dans la suite de l'exercice, on se place dans le repère orthonormé $\left(\text{O},\vec{\imath},\vec{\jmath},\vec{k}\right)$. Les coordonnées des différents points sont les suivantes : A(4;0;0), B(4;5;0), C(0;5;0), E(4;0;2, 5), F(4;5;2,5), G(0;5;2,5), S(0;0;3,5), U(0;0;6) et V(0;8;6). On souhaite déterminer de façon exacte la section des faces visibles de la véranda par le plan (UV K) qui sépare les zones ombragée et ensoleillée.
   1. Au moment le plus ensoleillé, le point K a pour abscisse $1,2$. Vérifier que les coordonnées du point K sont (1,2;0;3,2).
   On a $S(0;0;3,5)$ et $E(4;0;2,5)$.
   Ainsi $\vec{SE}(4;0;-1)$.
   Une représentation paramétrique de la droite $(SE)$ est donc :
   $\begin{cases}x=4t\\y=0\\z=3,5-t\end{cases} \qquad t\in \mathbb R$.
   On sait que l’abscisse du point $K$ est $1,2$ et qu’il appartient à la droite $(SE)$.
   On doit donc résoudre l’équation $4t=1,2$ soit $t=0,3$.
   En reportant cette valeur dans la représentation paramétrique de la droite $(SE)$ on trouve :
   $\begin{cases} x=1,2\\y=0\\z=3,2\end{cases}$
   Donc $K(1,2;0;3,2)$.
   $\quad$
   
   2. Montrer que le vecteur $ \vec{n}$ de coordonnées (7;0;3) est un vecteur normal au plan (UVK) et en déduire une équation cartésienne du plan (UVK).
   On a $\vec{UV}(0;8;0)$ et $\vec{UK}(1,2;0;-2,8)$
   Ces deux vecteurs du plan $(UVK)$ ne sont clairement pas colinéaires.
   $\vec{n}.\vec{UV}=0+0+0=0$
   $\vec{n}.\vec{UK}=8,4+0-8,4=0$
   Le vecteur $\vec{n}$ est donc orthogonal à deux vecteurs non colinéaires du plan $(UVK)$.
   Il est donc normal au plan $(UVK)$.
   $\quad$
   Une équation cartésienne de ce plan est de la forme $7x+3z+d=0$.
   On sait que les coordonnées du point $U(0;0;6)$ vérifient cette équation.
   Ainsi $0+18+d=0 \iff d=-18$
   Une équation cartésienne du plan $(UVK)$ est alors $7x+3z-18=0$.
   $\quad$
   
   3. Déterminer les coordonnées du point N intersection du plan (UVK) avec la droite (FG).
   $\vec{FG}(-4;0;0)$.
   Une représentation paramétrique de la droite $(FG)$ est donc :
   $\begin{cases} x=4-4k\\y=5\\z=2,5\end{cases} \qquad k\in\mathbb R$
   Le point $N$ appartient au plan $(UVK)$ et à la droite $(FG)$.
   Ses coordonnées sont donc solution du système suivant :
   $\begin{align*} \begin{cases} 7x+3z-18=0 \\x=4-4k\\y=5\\z=2,5\end{cases} &\iff \begin{cases} 28-28k+7,5-18=0\\x=4-4k\\y=5\\z=2,5\end{cases} \\
   &\iff \begin{cases} -28k+17,5=0\\x=4-4k\\y=5\\z=2,5\end{cases} \\
   &\iff \begin{cases} k=\dfrac{17,5}{28} \\x=4-4k\\y=5\\z=2,5\end{cases} \\
   &\iff \begin{cases} k=\dfrac{5}{8} \\x=1,5\\y=5\\z=2,5\end{cases}
   \end{align*}$
   Ainsi $N(1,5;5;2,5)$.
   $\quad$
   
   4. Expliquer comment construire la ligne polygonale sur le schéma de la véranda.
   On construit donc la droite parallèle à $(EF)$ passant par le point $K$. Elle coupe le segment $[SF]$ en $M$.
   On trace le segment $[MN]$.
   On trace la droite parallèle à la droite $(UK)$ passant par le point $N$. Elle coupe le segment $[BC]$ en $P$.
   On trace le segment $[NP]$.
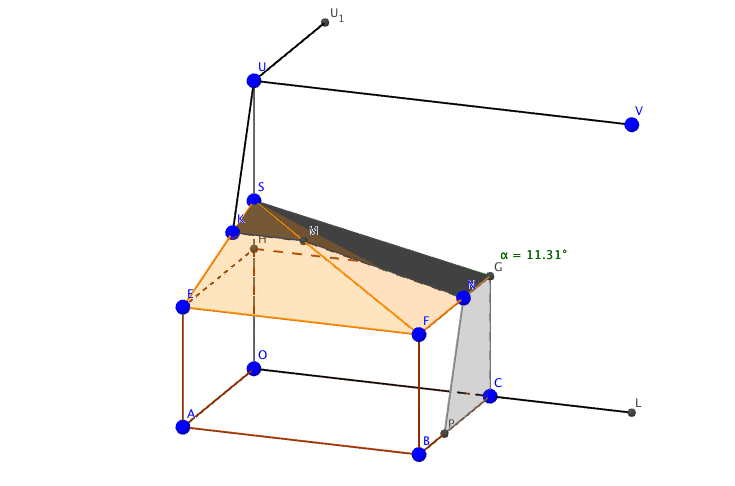
   $\quad$
3. Afin de faciliter l'écoulement des eaux de pluie, l'angle du segment [SG] avec l'horizontale doit être supérieur à 7 °. Cette condition est-elle remplie ?
On appelle $H$ le point du segment $[SO]$ tel que le triangle $SGH$ soit rectangle en $H$.
On a ainsi $SH=3,5-2,5=1$ et $HG=OC=5$.
Ainsi $\tan \widehat{SGH}=\dfrac{SH}{HG}=\dfrac{1}{5}$
Par conséquent $\widehat{SGH}\approx 11,3$°$>7$°.
La condition est donc bien remplie.
$\quad$