Baccalauréat STI 2D/STL spécialité SPCL Métropole- La Réunion 8 septembre 2016 - Correction Exercice 3
Page 6 sur 8
Correction de l'exercice 3 (3 points)
Pour chacune des 3 propositions suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse. Il est attribué un point par réponse exacte correctement justifiée. Une réponse non justifiée n'est pas prise en compte. Une absence de réponse n'est pas pénalisée.Indiquer sur la copie le numéro de la proposition, la réponse correspondante et la justification.
- Proposition 1 : $e^{\mathrm{i}\frac{\pi}4{}}+e^{\mathrm{i}\frac{3\pi}4{}}=\mathrm{i}\sqrt{2}$. $$\begin{array}{rl} e^{\mathrm{i}\frac{\pi}4{}}+e^{\mathrm{i}\frac{3\pi}4{}}&= \cos\left ( \frac{\pi}4{} \right ) + \mathrm{i} \sin\left ( \frac{\pi}4{} \right )+ \cos\left ( \frac{3\pi}4{} \right ) + \mathrm{i} \sin\left ( 3\frac{\pi}4{} \right ) \\ &= \dfrac{\sqrt 2 }{2} + \mathrm{i} \dfrac{\sqrt 2 }{2}-\dfrac{\sqrt 2 }{2} + \mathrm{i} \dfrac{\sqrt 2 }{2}\\ &=\mathrm{i}\sqrt 2 \end{array}$$ La proposition 1 est vraie.
- La durée de vie, en heures, d'un composant électronique est une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $\lambda = 5,5 \times 10^{-4}$ et dont la fonction de densité de probabilité est représentée ci-dessous.
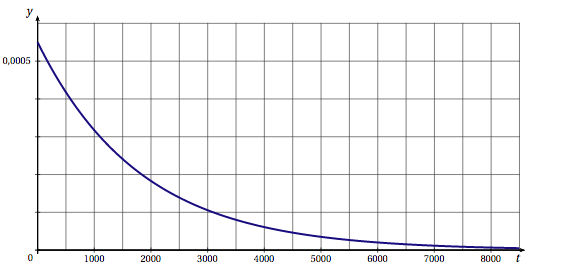
Proposition 2 : la probabilité, arrondie à 0,01 près, qu'un composant électronique pris au hasard ait une durée de vie inférieure à 1000 heures est 0,35. La variable aléatoire $T$ suit la loi exponentielle de paramètre $\lambda =5,5\times 10^{-4}$ d'où : $$\begin{array}{rl} P(T\leq 1000 ) &= \displaystyle \int_0^{10200}\lambda\text{e}^{-\lambda t}\;\text{d}t \\ &= \left [ -\text{e}^{-\lambda t}\right ]_0^{1000}\\ &=-\text{e}^{-1000 \lambda }-\left (-\text{e}^{0}\right )\\ &= 1- \text{e}^{-1000 \times 5,5\times 10^{-4} }\\ &= 1-\text{e}^{-0,55 }\\ &\approx 0, 423 \end{array}$$ La proposition 2 est fausse.
- Proposition 3 : la valeur moyenne de la fonction $f$ définie sur l'intervalle $\left[\dfrac{\pi}{2} ; \pi\right]$ par $f (x) = \cos(x)$ est $-\dfrac{2}{\pi}$.
On rappelle que la valeur moyenne $\mu$d'une fonction $f$ définie et continue sur un intervalle $[a ; b]$ est donnée par la formule :\[\mu = \dfrac{1}{b-a}\displaystyle\int_{a}^{b}f(x)\mathrm{d} x.\] La valeur moyenne de la fonction $f$ définie sur l'intervalle $\left[\dfrac{\pi}{2} ; \pi\right]$ par $f (x) = \cos(x)$ est : $$\begin{array}{rl} \mu &= \dfrac{1}{\pi -\dfrac{\pi}{2}}\displaystyle\int_{\dfrac{\pi}{2}}^{\pi }\cos x \mathrm{d} x \\ &= \left [ \sin x \right ]_{\dfrac{\pi}{2}} ^{\pi }\\ &=\dfrac{2}{\pi }\left ( \sin \pi-\sin\left (\dfrac{\pi}{2}\right )\right )\\ &= \dfrac{2}{\pi } ( 0-1)\\ &=- \dfrac{2}{\pi } \end{array}$$ La proposition 3 est vraie.
Exercice 4
- Vues: 22181
