Baccalauréat STI 2D/STL spécialité SPCL Nouvelle-Calédonie 27 novembre 2018 - Exercice 2

Page 3 sur 8: Exercice 2

Exercice 2 5 points

Probabilités

Les trois parties de cet exercice peuvent être traitées de façon indépendante. Dans cet exercice, les résultats seront arrondis au millième.
La société Héliocel fabrique des cellules photovoltaïques destinées à être assemblées pour former des panneaux solaires qui seront ensuite installés sur le toit d'habitations pour produire de l'électricité.

Partie A

On estime que 5 % des cellules fabriquées par Héliocel présentent un défaut et sont donc inutilisables.
On prélève au hasard un lot de $80$ cellules dans la production pour vérification. Le nombre de cellules produites est suffisamment important pour que l'on assimile ce prélèvement à un tirage avec remise de $80$ cellules. On appelle $X$ la variable aléatoire qui, à chaque lot de $80$ cellules, associe le nombre de cellules inutilisables.

1. La variable aléatoire $X$ suit une loi binomiale. Préciser ses paramètres.
2. Quelle est la probabilité qu'un lot ne contienne aucune cellule inutilisable ?
3. Un panneau solaire est constitué de $75$ cellules. Quelle est la probabilité d'avoir assez de cellules sans défaut dans un seul lot pour pouvoir fabriquer un panneau ?

 

Partie B

Après amélioration sur sa chaîne de fabrication, la société annonce une proportion de 3 % de cellules inutilisables. Afin de vérifier cette annonce, le responsable qualité prélève de manière aléatoire un échantillon de $180$ cellules et observe que $9$ cellules sont inutilisables. Cette observation remet-elle en cause l'annonce de la société ?

Partie C

Une famille décide d'installer 15 de ces panneaux solaires sur le toit de sa maison pour produire de l'électricité. La production électrique dépend de l'ensoleillement. On appelle $Y$ la variable aléatoire qui, à chaque journée, associe la production électrique (en kWh) fournie par ces 15 panneaux. On admet que la variable aléatoire $Y$ suit la loi normale d'espérance $\mu = 9$ et d'écart-type $\sigma = 3$.

1. Quelle est la probabilité que la production journalière de l'installation de cette famille soit comprise entre $6$ kWh et $12$ kWh ?
2. Parmi les trois fonctions de densité de probabilité représentées ci-dessous, laquelle peut être celle de la loi de $Y$ ? Justifier.
   
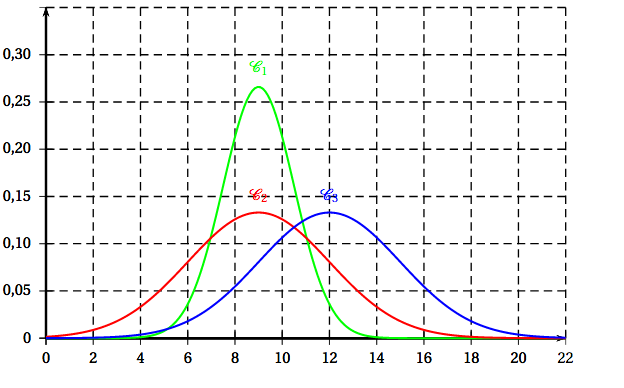
3. La consommation moyenne de cette famille est $13$ kWh/jour. Quelle est la probabilité que la production journalière de son installation soit supérieure à sa consommation moyenne quotidienne ?