Baccalauréat S Nouvelle-Calédonie Wallis et Futuna 28 novembre 2017
Exercice 1 4 points
Sofia souhaite se rendre au cinéma. Elle peut y aller à vélo ou en bus.
Partie A : En utilisant le bus
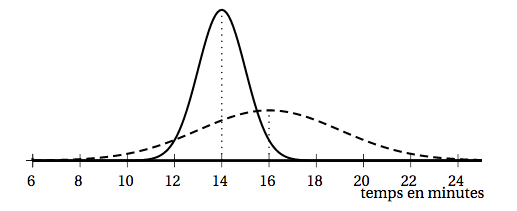
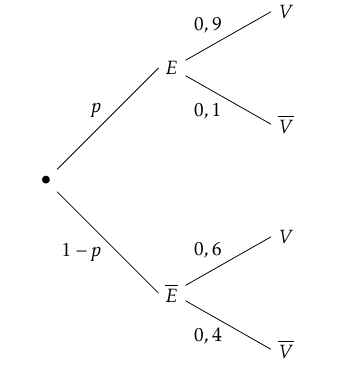
On suppose dans cette partie que Sofia utilise le bus pour se rendre au cinéma. La durée du trajet entre son domicile et le cinéma (exprimée en minutes) est modélisée par la variable aléatoire $T_B$ qui suit la loi uniforme sur $[12~;~15]$.
- Démontrer que la probabilité que Sofia mette entre $12$ et $14$ minutes est de $\dfrac23$.
- Donner la durée moyenne du trajet.
Partie B : En utilisant son vélo
On suppose à présent que Sofia choisit d'utiliser son vélo. La durée du parcours (exprimée en minutes) est modélisée par la variable aléatoire $T_v$ qui suit la loi normale d'espérance $\mu = 14$ et d'écart-type $\sigma=1,5$.
- Quelle est la probabilité que Sofia mette moins de $14$ minutes pour se rendre au cinéma ? Quelle est la probabilité que Sofia mette entre $12$ et $14$ minutes pour se rendre au cinéma ? On arrondira le résultat à $10^{-3}$.
- Démontrer que la probabilité, arrondie à $10^{-2}$, que Sofia mette entre $12$ et $14$ minutes est de $0,49$.
Partie C : En jouant aux dés
Sofia hésite entre le bus et le vélo. Elle décide de lancer un dé équilibré à $6$ faces. Si elle obtient $1$ ou $2$, elle prend le bus, sinon elle prend son vélo. On note :
- $B$ l'évènement « Sofia prend le bus » ;
- $V$ l'évènement « Sofia prend son vélo » ;
- $C$ l'évènement « Sofia met entre 12 et 14 minutes pour se rendre au cinéma ».
- Sachant que Sofia a mis entre $12$ et $14$ minutes pour se rendre au cinéma, quelle est la probabilité, arrondie à $10^{-2}$, qu'elle ait emprunté le bus ? $\quad$
Correction de l'exercice 1 (4 points)
Sofia souhaite se rendre au cinéma. Elle peut y aller à vélo ou en bus.
Partie A : En utilisant le bus
On suppose dans cette partie que Sofia utilise le bus pour se rendre au cinéma. La durée du trajet entre son domicile et le cinéma (exprimée en minutes) est modélisée par la variable aléatoire $T_B$ qui suit la loi uniforme sur $[12~;~15]$.
- Démontrer que la probabilité que Sofia mette entre $12$ et $14$ minutes est de $\dfrac23$. On veut calculer $p\left(12 \leq T_B \leq 14\right)=\dfrac{14-12}{15-12}=\dfrac{2}{3}$
- Donner la durée moyenne du trajet. La durée moyenne du trajet est $E\left(T_B\right)=\dfrac{12+15}{2}=13,5$ min $=13$min $30$s
$\quad$
$\quad$
Partie B : En utilisant son vélo
On suppose à présent que Sofia choisit d'utiliser son vélo. La durée du parcours (exprimée en minutes) est modélisée par la variable aléatoire $T_v$ qui suit la loi normale d'espérance $\mu = 14$ et d'écart-type $\sigma=1,5$.
- Quelle est la probabilité que Sofia mette moins de $14$ minutes pour se rendre au cinéma ? Quelle est la probabilité que Sofia mette entre $12$ et $14$ minutes pour se rendre au cinéma ? On arrondira le résultat à $10^{-3}$. On veut calculer $p\left(T_V\leq 14\right)=0,5$ car $\mu=14$.
- Démontrer que la probabilité, arrondie à $10^{-2}$, que Sofia mette entre $12$ et $14$ minutes est de $0,49$. D’après la calculatrice $p\left(12\leq Tv\leq 14\right)\approx 0,409$
$\quad$
$\quad$
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
Partie C : En jouant aux dés
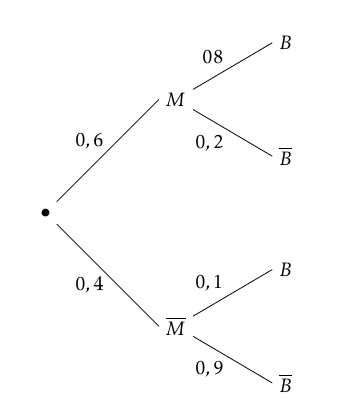
Sofia hésite entre le bus et le vélo. Elle décide de lancer un dé équilibré à $6$ faces. Si elle obtient $1$ ou $2$, elle prend le bus, sinon elle prend son vélo. On note :
- $B$ l'évènement « Sofia prend le bus » ;
- $V$ l'évènement « Sofia prend son vélo » ;
- $C$ l'évènement « Sofia met entre 12 et 14 minutes pour se rendre au cinéma ».
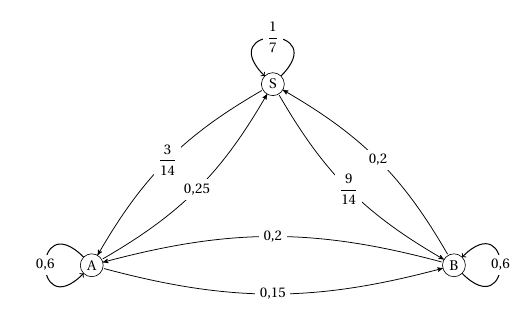
- Sachant que Sofia a mis entre $12$ et $14$ minutes pour se rendre au cinéma, quelle est la probabilité, arrondie à $10^{-2}$, qu'elle ait emprunté le bus ? La probabilité d’obtenir 1 ou 2 avec le dé est $\dfrac{2}{6}=\dfrac{1}{3}$.
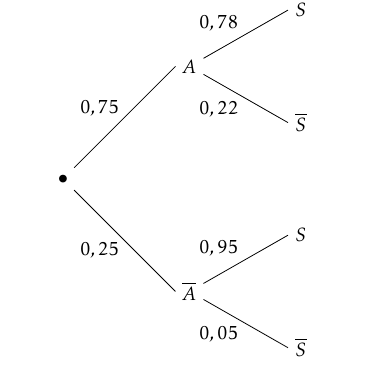
Un arbre pondéré représentant la situation est donc :
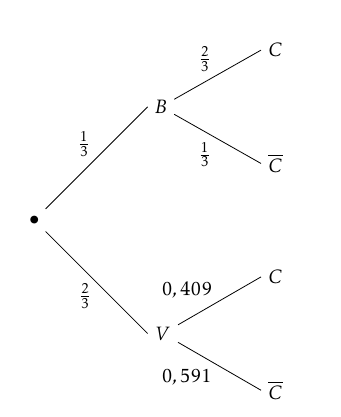 D’après la formule des probabilités totales on a :
D’après la formule des probabilités totales on a :$\begin{align*} p(C)&=p(B\cap C)+p(V\cap V)\\
&=\dfrac{1}{3}\times \dfrac{2}{3}+\dfrac{2}{3}\times 0,409 \\
&\approx 0,49
\end{align*}$
Exercice 2 (5 points)
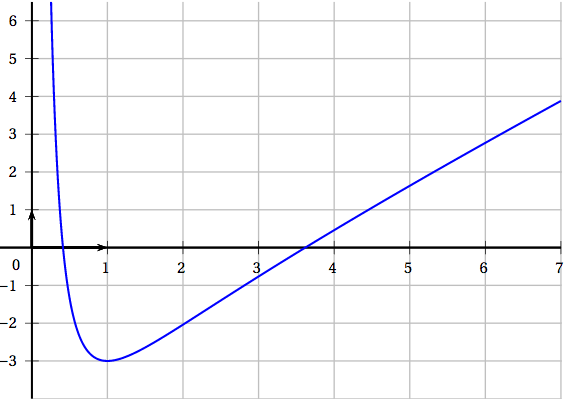
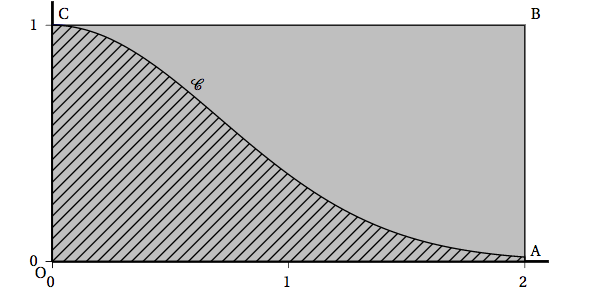
On considère la fonction $f$ définie sur $]0~;~+\infty[$ par $$f(x)=\dfrac{\big(\ln x\big)^2}x.$$ On note $\mathcal C$ la courbe représentative de $f$ dans un repère orthonormé.
- Déterminer la limite en $0$ de la fonction $f$ et interpréter graphiquement le résultat.
-
- Démontrer que, pour tout $x$ appartenant à $]0~;~+\infty[$, \[f(x)=4\left(\dfrac{\ln\big(\sqrt x\big)}{\sqrt x}\right)^2.\]
- En déduire que l'axe des abscisses est une asymptote à la courbe représentative de la fonction $f$ au voisinage de $+ \infty$.
- On admet que $f$ est dérivable sur $]0~;~+\infty[$ et on note $f'$ sa fonction dérivée.
- Démontrer que, pour tout $x$ appartenant à $]0~;~+\infty[$, \[f'(x)=\dfrac{\ln(x)\big(2-\ln(x)\big)}{x^2}.\]
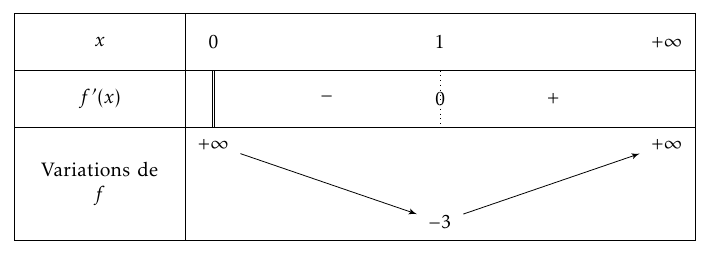
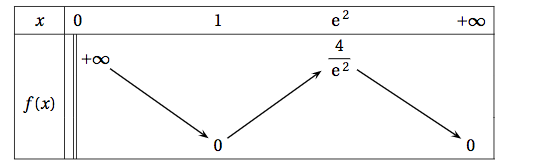
- Étudier le signe de $f'(x)$ selon les valeurs du nombre réel $x$ strictement positif.
- Calculer $f(1)$ et $f\big(\text{e}^2\big)$.
- Démontrer que l'équation $f(x) = 1$ admet une unique solution $\alpha$ sur $]0~;~+\infty[$ et donner un encadrement de $\alpha$ d'amplitude $10^{-2}$.
Correction de l'exercice 2 (5 points)
On considère la fonction $f$ définie sur $]0~;~+\infty[$ par $$f(x)=\dfrac{\big(\ln x\big)^2}x.$$ On note $\mathcal C$ la courbe représentative de $f$ dans un repère orthonormé.
- Déterminer la limite en $0$ de la fonction $f$ et interpréter graphiquement le résultat. $\lim\limits_{x \to 0^+} \ln x=-\infty$ donc $\lim\limits_{X \to 0^+} \left(\ln x\right)^2=+\infty$
-
- Démontrer que, pour tout $x$ appartenant à $]0~;~+\infty[$, \[f(x)=4\left(\dfrac{\ln\big(\sqrt x\big)}{\sqrt x}\right)^2.\]
- En déduire que l'axe des abscisses est une asymptote à la courbe représentative de la fonction $f$ au voisinage de $+ \infty$. $\lim\limits_{x \to +\infty} \sqrt{x}=+\infty$ et $\lim\limits_{X \to +\infty} \dfrac{\ln X}{X}=0$ donc $\lim\limits_{x \to +\infty} \dfrac{\ln\left(\sqrt{x}\right)}{\sqrt{x}}=0$
$\quad$ $\begin{align*} 4\left(\dfrac{\ln\left(\sqrt{x}\right)}{\sqrt{x}}\right)^2 &=4\left(\dfrac{\dfrac{1}{2}\ln x}{\sqrt{x}}\right)^2 \\
&=4\times \dfrac{\dfrac{1}{4}\left(\ln x\right)^2}{x} \\
&=f(x)
\end{align*}$
$\quad$
Ainsi $\lim\limits_{x \to +\infty} f(x)=0$, et on déduit donc que l'axe des abscisses est une asymptote à la courbe représentative de la fonction $f$ au voisinage de $+ \infty$. - On admet que $f$ est dérivable sur $]0~;~+\infty[$ et on note $f'$ sa fonction dérivée.
- Démontrer que, pour tout $x$ appartenant à $]0~;~+\infty[$, \[f'(x)=\dfrac{\ln(x)\big(2-\ln(x)\big)}{x^2}.\] $\begin{align*} f'(x)&=\dfrac{2x\times \dfrac{1}{x}\times \ln x-\left(\ln x\right)^2}{x^2} \\
- Étudier le signe de $f'(x)$ selon les valeurs du nombre réel $x$ strictement positif. $2-\ln(x)=0 \iff x=\text{e}^2$ et $2-\ln(x)>0 \iff 2>\ln(x)\iff \text{e}^2>x$
- Calculer $f(1)$ et $f\big(\text{e}^2\big)$.
&=\dfrac{2\ln x-\left(\ln x\right)^2}{x^2} \\
&=\dfrac{\ln(x)\left(2-\ln(x)\right)}{x^2}
\end{align*}$
$\quad$
Le signe de $f'(x)$ ne dépend que du signe de $\ln(x)\left(2-\ln(x)\right)$.
On obtient ainsi le tableau de signe suivant :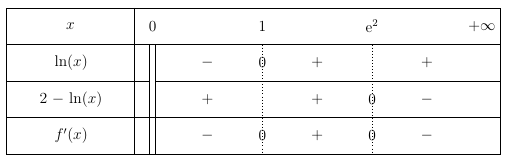
 $\ln(1)=0$ donc $f(1)=0$
$\ln(1)=0$ donc $f(1)=0$ - Démontrer que l'équation $f(x) = 1$ admet une unique solution $\alpha$ sur $]0~;~+\infty[$ et donner un encadrement de $\alpha$ d'amplitude $10^{-2}$. La fonction $f$ est continue (car dérivable) et strictement décroissante sur l’intervalle $]0;1]$.
$\lim\limits_{X \to 0^+} \dfrac{1}{x}=+\infty$ donc $\lim\limits_{X \to 0^+} f(x)=+\infty$.
$\quad$
$f\left(\text{e}^2\right)=\dfrac{\ln\left(\text{e}^2\right)^2}{\text{e}^2}=\dfrac{2^2}{\text{e}^2}=\dfrac{4}{\text{e}^2}$
$\quad$
$\lim\limits_{x \to 0^+}f(x)=+\infty$ et $f(1)=0$
Donc $1\in [0;+\infty[$
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires), l’équation $f(x)=1$ possède une unique solution $\alpha$ sur l’intervalle $]0;1]$.
Sur l’intervalle $[1;+\infty[$ on a $f(x)\leq \dfrac{4}{\text{e}^2}<1$. L’équation $f(x)=1$ ne possède donc pas de solution sur cet intervalle.
$\quad$
Cela signifie par conséquent que l’équation $f(x)=1$ possède une unique solution $\alpha$ sur $]0;+\infty[$ et $\alpha \in ]0,49;0,50[$ d’après la calculatrice.
$\quad$
Exercice 3 (3 points)
Les deux parties de cet exercice sont indépendantes.
Partie A
Soit la fonction $f$ définie sur l'ensemble des nombres réels par \[f(x) = 2\text{e}^x-\text{e}^{2x}\] et $\mathcal C$ sa représentation graphique dans un repère orthonormé. On admet que, pour tout $x$ appartenant à $[0~;~\ln(2)]$, $f(x)$ est positif. Indiquer si la proposition suivante est vraie ou fausse en justifiant votre réponse.
Proposition A :
L'aire du domaine délimité par les droites d'équations $x=0$ et $x = \ln (2)$, l'axe des abscisses et la courbe $\mathcal C$ est égale à $1$ unité d'aire.
Partie B
Soit $n$ un entier strictement positif. Soit la fonction $f_n$ définie sur l'ensemble des nombres réels par $$f_n(x) = 2n\text{e}^x-\text{e}^{2x}$$ et $\mathcal C_n$ sa représentation graphique dans un repère orthonormé. On admet que $f_n$ est dérivable et que $\mathcal C_n$ admet une tangente horizontale en un unique point $S_n$. Indiquer si la proposition suivante est vraie ou fausse en justifiant votre réponse.
Proposition B :
Pour tout entier strictement positif $n$, l'ordonnée du point $S_n$ est $n^2$.
Correction de l'exercice 3 (3 points)
Les deux parties de cet exercice sont indépendantes.
Partie A
Proposition A :
L'aire du domaine délimité par les droites d'équations $x=0$ et $x = \ln (2)$, l'axe des abscisses et la courbe $\mathcal C$ est égale à $1$ unité d'aire.
Fausse
La fonction $f$ est positive sur l’intervalle $\left[0;\ln(2)\right]$. On veut donc calculer :
$\begin{align*}I&=\displaystyle \int_0^{\ln(2)} f(x)\text{d}x \\
&=\left[2\text{e}^x-\dfrac{1}{2}\text{e}^{2x}\right]_0^{\ln 2} \\
&=2\times 2-\dfrac{1}{2}\times 2^2-\left(2-\dfrac{1}{2}\right) \\
&=\dfrac{1}{2}\\
&\neq 1
\end{align*}$
$\quad$
Partie B
Proposition B :
Pour tout entier strictement positif $n$, l'ordonnée du point $S_n$ est $n^2$.
Proposition B vraie
La fonction $f_n$ est dérivable sur $\mathbb{R}$ en tant que somme de fonctions dérivables sur cet intervalle.
$\begin{align*} {f_n}'(x)&=2n\text{e}^x-2\text{e}^{2x} \\
&=2\text{e}^x\left(n-\text{e}^x\right)
\end{align*}$
La fonction exponentielle est strictement positive donc ${f_n}'(x)=0 \iff n=\text{e}^x \iff x=\ln(n)$
$f\left(\ln(n)\right)=2n\times n-n^2=n^2$
$\quad$
Exercice 4 3 points
Les questions 1. et 2. de cet exercice pourront être traitées de manière indépendante.
On considère la suite des nombres complexes $\left(z_n\right)$ définie pour tout entier naturel $n$ par \[z_n = \dfrac{1 + \text{i}}{(1-\text{i})^n}.\] On se place dans le plan complexe d'origine O.
- Pour tout entier naturel $n$, on note $A_n$ le point d'affixe $z_n$.
- Démontrer que, pour tout entier naturel $n$, $\dfrac{z_{n+4}}{z_n}$ est réel.
- Démontrer alors que, pour tout entier naturel $n$, les points O, $A_n$ et $A_{n+4}$ sont alignés.
- Pour quelles valeurs de $n$ le nombre $z_n$ est-il réel ?
Correction de l'exercice 4 5 points
Les questions 1. et 2. de cet exercice pourront être traitées de manière indépendante.
On considère la suite des nombres complexes $\left(z_n\right)$ définie pour tout entier naturel $n$ par \[z_n = \dfrac{1 + \text{i}}{(1-\text{i})^n}.\] On se place dans le plan complexe d'origine O.
- Pour tout entier naturel $n$, on note $A_n$ le point d'affixe $z_n$.
- Démontrer que, pour tout entier naturel $n$, $\dfrac{z_{n+4}}{z_n}$ est réel. $z_{n+4}=\dfrac{1+\text{i}}{(1-\text{i})^n(1-\text{i})^4}=\dfrac{1+\text{i}}{-4(1-\text{i})^n}=\dfrac{-1}{4}z_n$
- Démontrer alors que, pour tout entier naturel $n$, les points O, $A_n$ et $A_{n+4}$ sont alignés. Un argument de $\dfrac{z_{n+4}}{z_n}$ est donc $\pi$.
Par conséquent $\dfrac{z_{n+4}}{z_n}=-\dfrac{1}{4}$.
$\quad$
Or $\left(\vec{OA_n},\vec{OA_{n+4}}\right)=$arg$\left(\dfrac{z_{n+4}}{z_n}\right)+2k\pi=\pi+2k\pi$
Les points $O,A_n$ et $A_{n+4}$ sont donc alignés.
$\quad$ - Pour quelles valeurs de $n$ le nombre $z_n$ est-il réel ? $|1+\text{i}|=\sqrt{2}$ donc $1+\text{i}=\sqrt{2}\left(\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}\text{i}\right)=\sqrt{2}\text{e}^{\text{i}\pi/4}$
De même $1-\text{i}=\sqrt{2}\text{e}^{-\text{i}\pi/4}$
Ainsi $z_n=\dfrac{\sqrt{2}\text{e}^{\text{i}\pi/4}}{\left(\sqrt{2}\text{e}^{-\text{i}\pi/4}\right)^n}=\sqrt{2}^{1-n}\text{e}^{\text{i}(n+1)\pi/4}$
$z_n$ est réel si, et seulement si, $n+1=4k$ avec $k\in \mathbb{Z}$
si, et seulement si, $n=4k-1$ avec $k\in \mathbb{Z}$
Exercice 5 5 points
Soit $\left(u_n\right)$ la suite définie par $u_0 = 3$, $u_1 = 6$ et, pour tout entier naturel $n$ : \[u_{n+2} = \dfrac{5}{4}u_{n+1} - \dfrac{1}{4}u_n.\] Le but de cet exercice est d'étudier la limite éventuelle de la suite $\left(u_n\right)$.
Partie A :
On souhaite calculer les valeurs des premiers termes de la suite $\left(u_n\right)$ à l'aide d'un tableur. On a reproduit ci-dessous une partie d'une feuille de calcul, où figurent les valeurs de $u_0$ et de $u_1$. $$ \begin{array}{ | c|c|c|}\hline &A &B\\ \hline 1 & n & u_n \\ \hline 2 &0 &3\\ \hline 3 &1 &6\\ \hline 4 &2 &\\ \hline 5 &3 &\\ \hline 6 &4 &\\ \hline 7 &5 &\\ \hline \end{array} $$
- Donner une formule qui, saisie dans la cellule B4, puis recopiée vers le bas, permet d'obtenir des valeurs de la suite $\left(u_n\right)$ dans la colonne B.
- Recopier et compléter le tableau ci-dessus. On donnera des valeurs approchées à $10^{-3}$ près de $u_n$ pour $n$ allant de 2 à 5.
- Que peut-on conjecturer à propos de la convergence de la suite $\left(u_n\right)$ ?
Partie B : Étude de la suite
On considère les suites $\left(v_n\right)$ et $\left(w_n\right)$ définies pour tout entier naturel $n$ par : \[v_n = u_{n + 1} - \dfrac{1}{4}u_n\quad \text{ et }\quad w_n = u_n - 7.\]
-
- Démontrer que $\left(v_n\right)$ est une suite constante.
- En déduire que, pour tout entier naturel $n$, $u_{n+1} = \dfrac{1}{4}u_n + \dfrac{21}{4}$.
-
- En utilisant le résultat de la question 1. b. , montrer par récurrence que, pour tout entier naturel $n$, $u_n < u_{n+1} < 15$.
- En déduire que la suite $\left(u_n\right)$ est convergente.
-
- Démontrer que $\left(w_n\right)$ est une suite géométrique dont on précisera le premier terme et la raison.
- En déduire que, pour tout entier naturel $n$, $u_n = 7 - \left(\dfrac{1}{4} \right)^{n-1}$.
- Calculer la limite de la suite $\left(u_n\right)$.
Correction de l'exercice 5 5 points
Soit $\left(u_n\right)$ la suite définie par $u_0 = 3$, $u_1 = 6$ et, pour tout entier naturel $n$ : \[u_{n+2} = \dfrac{5}{4}u_{n+1} - \dfrac{1}{4}u_n.\] Le but de cet exercice est d'étudier la limite éventuelle de la suite $\left(u_n\right)$.
Partie A :
On souhaite calculer les valeurs des premiers termes de la suite $\left(u_n\right)$ à l'aide d'un tableur. On a reproduit ci-dessous une partie d'une feuille de calcul, où figurent les valeurs de $u_0$ et de $u_1$. $$ \begin{array}{ | c|c|c|}\hline &A &B\\ \hline 1 & n & u_n \\ \hline 2 &0 &3\\ \hline 3 &1 &6\\ \hline 4 &2 &\\ \hline 5 &3 &\\ \hline 6 &4 &\\ \hline 7 &5 &\\ \hline \end{array} $$
- Donner une formule qui, saisie dans la cellule B4, puis recopiée vers le bas, permet d'obtenir des valeurs de la suite $\left(u_n\right)$ dans la colonne B. On peut saisir $=5/4*B3-B2/4$
- Recopier et compléter le tableau ci-dessus. On donnera des valeurs approchées à $10^{-3}$ près de $u_n$ pour $n$ allant de 2 à 5. On obtient le tableau suivant :
- Que peut-on conjecturer à propos de la convergence de la suite $\left(u_n\right)$ ? Il semblerait donc que la suite $\left(u_n\right)$ converge vers $7$.
$\quad$
$\begin{array}{|c|c|c|}
\hline
&\text{A}&\text{B}\\
\hline
1&n&u_n\\
\hline
2&0&3\\
\hline
3&1&6\\
\hline
4&2&\boldsymbol{6,75}\\
\hline
5&3&\boldsymbol{6,938}\\
\hline
6&4&\boldsymbol{6,984}\\
\hline
7&5&\boldsymbol{6,996}\\
\hline
\end{array}$
$\quad$
Partie B : Étude de la suite
On considère les suites $\left(v_n\right)$ et $\left(w_n\right)$ définies pour tout entier naturel $n$ par : \[v_n = u_{n + 1} - \dfrac{1}{4}u_n\quad \text{ et }\quad w_n = u_n - 7.\]
-
- Démontrer que $\left(v_n\right)$ est une suite constante. Pour tout entier naturel $n$ on a :
- En déduire que, pour tout entier naturel $n$, $u_{n+1} = \dfrac{1}{4}u_n + \dfrac{21}{4}$. Ainsi, pour tout entier naturel $n$ on a :
$\begin{align*} v_{n+1}&=u_{n+2}-\dfrac{1}{4}u_{n+1}\\
&=\dfrac{5}{4}u_{n+1}-\dfrac{1}{4}u_n-\dfrac{1}{4}u_{n+1}\\
&=u_{n+1}-\dfrac{1}{4}u_n\\
&=v_n
\end{align*}$
La suite $\left(v_n\right)$ est donc constante et $v_0=u_1-\dfrac{u_0}{4}=\dfrac{21}{4}$.
$\quad$
$\dfrac{21}{4}=u_{n+1}-\dfrac{1}{4}u_n \iff u_{n+1}=\dfrac{1}{4}u_n+\dfrac{21}{4}$.
$\quad$ -
- En utilisant le résultat de la question 1. b. , montrer par récurrence que, pour tout entier naturel $n$, $u_n < u_{n+1} < 15$. Initialisation : Si $n=0$. On a $u_0=3$ et $u_1=6$ donc $u_0<u_1<15$
- En déduire que la suite $\left(u_n\right)$ est convergente. La suite $\left(u_n\right)$ est croissante et majorée par $15$; elle est donc convergente.
La propriété est vraie au rang $0$
$\quad$
Hérédité : On suppose la propriété vraie au rang $n$ : $u_n<u_{n+1}<15$
Montrons qu’elle est encore vraie au rang $n+1$, c’est-à-dire que $u_{n+1}<u_{n+2}<15$
$\begin{align*} u_n<u_{n+1}<15 &\iff \dfrac{1}{4}u_n<\dfrac{1}{4}u_{n+1}<\dfrac{15}{4} \\
&\iff \dfrac{1}{4}u_n+\dfrac{21}{4}<\dfrac{1}{4}u_{n+1}+\dfrac{21}{4}<\dfrac{15}{4}+\dfrac{21}{4} \\
&\iff u_{n+1}<u_{n+2}<9<15
\end{align*}$
La propriété est donc vraie au rang $n+1$
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ on a $u_n<u_{n+1}<15$.
$\quad$
$\quad$ -
- Démontrer que $\left(w_n\right)$ est une suite géométrique dont on précisera le premier terme et la raison. Pour tout entier naturel $n$ on a :
- En déduire que, pour tout entier naturel $n$, $u_n = 7 - \left(\dfrac{1}{4} \right)^{n-1}$. Ainsi pour tout entier naturel $n$ on a $w_n=-4\times \left(\dfrac{1}{4}\right)^n=-\left(\dfrac{1}{4}\right)^{n-1}$
- Calculer la limite de la suite $\left(u_n\right)$. $-1<\dfrac{1}{4}<1$ donc $\lim\limits_{n \to +\infty} \left(\dfrac{1}{4}\right)^{n-1}=0$.
$\begin{align*} w_n&=u_{n+1}-7 \\
&=\dfrac{1}{4}u_n+\dfrac{21}{4}-7\\
&=\dfrac{1}{4}u_n-\dfrac{7}{4} \\
&=\dfrac{1}{4}\left(u_n-7\right) \\
&=\dfrac{1}{4}w_n
\end{align*}$
La suite $\left(w_n\right)$ est donc géométrique de raison $\dfrac{1}{4}$ et de premier terme $w_0=3-7=-4$
$\quad$
Or $w_n=u_n-7$ donc $u_n=w_n+7=7-\left(\dfrac{1}{4}\right)^{n-1}$
$\quad$
Par conséquent $\lim\limits_{n \to +\infty} u_n=7$.
Spécialité 5 points
Dans un territoire donné, on s'intéresse à l'évolution couplée de deux espèces : les buses (les prédateurs) et les campagnols (les proies). Des scientifiques modélisent, pour tout entier naturel $n$, cette évolution par : \[\left\{\begin{array}{rcl} b_0 &=& 1000 \\ c_0 &=& 1500 \\ b_{n+1} &=&\ - 0,3 b_n + 0,5c_n\\ c_{n+1} &=&- 0,5b_n +1,3c_n \end{array}\right.\] où $b_n$ représente approximativement le nombre de buses et $c_n$ le nombre approximatif de campagnols le $1^\text{er}$ juin de l'année $2000 + n$ (où $n$ désigne un entier naturel).
- On note $A$ la matrice $\begin{pmatrix} 0,3 & 0,5 \\ -0,5 & 1,3\end{pmatrix}$ et, pour tout entier naturel $n$, $U_n$ la matrice colonne $\begin{pmatrix} b_n \\ c_n \end{pmatrix}$.
- Vérifier que $U_1 = \begin{pmatrix} 1050 \\ 1450 \end{pmatrix}$ et calculer $U_2$.
- Vérifier que, pour tout entier naturel $n$, $U_{n+1} = AU_n$.
- On admet que $P$ a pour inverse une matrice $Q$ de la forme $\begin{pmatrix} 1 & 0 \\ a & 1\end{pmatrix}$ où $a$ est un réel.
- Déterminer la valeur de $a$ en justifiant.
- On admet que $A = PTQ$. Démontrer que, pour tout entier $n$ non nul, on a \[A^n=PT^nQ.\]
- Démontrer à l'aide d'un raisonnement par récurrence que, pour tout entier $n$ non nul, \[T^n=\begin{pmatrix} 0,8^n & 0,5n\times 0,8^{n - 1 } \\ 0 & 0,8^n \end{pmatrix}.\]
- Lucie exécute l'algorithme ci-dessous et obtient en sortie $N = 40$. Quelle conclusion Lucie peut-elle énoncer pour les buses et les campagnols ? $$\begin{array}{|rl|} \hline \text{Initialisation: }& N \text{prend la valeur } 0 \\ & B \text{ prend la valeur 1000} \\ & C \text{ prend la valeur 1500} \\ \text{Traitement :} & \text{Tant que } B > 2 \text{ ou } C > 2 \\ & \qquad N \text{ prend la valeur } N + 1 \\ & \qquad R \text{ prend la valeur }B \\ & \qquad B \text{ prend la valeur } - 0,3R + 0,5C \\ & \qquad C \text{ prend la valeur }- 0,5R + 1,3C \\ &\text{ Fin Tant Que} \\ \text{Sortie :} & \text{Afficher } N \\ \hline \end{array} $$
- On admet que, pour tout entier naturel $n$ non nul, on a \[U_n = \begin{pmatrix} 1000 \times 0,8^n +\dfrac{625}2n \times 0,8^n \\[.4cm] 1500 \times 0,8^n + \dfrac{625}2n \times 0,8^n \end{pmatrix} \] et \[n \leqslant 10 \times 1,1^n.\]
- En déduire les limites des suites $\left(b_n\right)$ et $\left(c_n\right)$.
- Des mesures effectuées dans des territoires comparables montrent que la population de campagnols reste toujours supérieure à au moins $50$ individus. À la lumière de ces informations, le modèle proposé dans l'exercice vous paraît-il cohérent ?
Correction de l'exercice de Spécialité 5 points
Dans un territoire donné, on s'intéresse à l'évolution couplée de deux espèces : les buses (les prédateurs) et les campagnols (les proies). Des scientifiques modélisent, pour tout entier naturel $n$, cette évolution par : \[\left\{\begin{array}{rcl} b_0 &=& 1000 \\ c_0 &=& 1500 \\ b_{n+1} &=&\ - 0,3 b_n + 0,5c_n\\ c_{n+1} &=&- 0,5b_n +1,3c_n \end{array}\right.\] où $b_n$ représente approximativement le nombre de buses et $c_n$ le nombre approximatif de campagnols le $1^\text{er}$ juin de l'année $2000 + n$ (où $n$ désigne un entier naturel).
- On note $A$ la matrice $\begin{pmatrix} 0,3 & 0,5 \\ -0,5 & 1,3\end{pmatrix}$ et, pour tout entier naturel $n$, $U_n$ la matrice colonne $\begin{pmatrix} b_n \\ c_n \end{pmatrix}$.
- Vérifier que $U_1 = \begin{pmatrix} 1050 \\ 1450 \end{pmatrix}$ et calculer $U_2$. On a $\begin{cases} b_1=0,3\times 1~000+0,5\times 1~500\\c_1=-0,5\times 1~000+1,3\times 1~500\end{cases}$ soit $\begin{cases} b_1=1~050\\c_1=1~450\end{cases}$
- Vérifier que, pour tout entier naturel $n$, $U_{n+1} = AU_n$. Pour tout entier naturel $n$ on a :
Ainsi $U_1=\begin{pmatrix}1~050\\1~450\end{pmatrix}$
$\quad$
$\begin{cases} b_{n+1}=0,3b_n+0,5c_n\\c_{n+1}=-0,5b_n+1,3c_n\end{cases} \iff \begin{pmatrix}b_{n+1}\\c_{n+1}\end{pmatrix}=\begin{pmatrix}0,3&0,5\\-0,5&1,3\end{pmatrix}\times \begin{pmatrix}b_n\\c_n\end{pmatrix}$ $\iff U_{n+1}AU_n$.
$\quad$ - On admet que $P$ a pour inverse une matrice $Q$ de la forme $\begin{pmatrix} 1 & 0 \\ a & 1\end{pmatrix}$ où $a$ est un réel.
- Déterminer la valeur de $a$ en justifiant. $Q$ est la matrice inverse de $P$ donc
- On admet que $A = PTQ$. Démontrer que, pour tout entier $n$ non nul, on a \[A^n=PT^nQ.\] Montrons par récurrence sur $n$ que $A^n=PT^nQ$.
- Démontrer à l'aide d'un raisonnement par récurrence que, pour tout entier $n$ non nul, \[T^n=\begin{pmatrix} 0,8^n & 0,5n\times 0,8^{n - 1 } \\ 0 & 0,8^n \end{pmatrix}.\]
$\begin{align*} PQ=\begin{pmatrix}1&0\\0&1\end{pmatrix} &\iff \begin{pmatrix}1&0\\1+a&1\end{pmatrix}=\begin{pmatrix}1&0\\0&1\end{pmatrix} \\
&\iff 1+a=0 \\
&\iff a=-1
\end{align*}$
$\quad$
Initialisation : il est admis que $A=PTQ$. La propriété est donc vraie au rang $1$.
$\quad$
Hérédité : On suppose la propriété vraie au rang $n$ : $A^n=PT^nQ$
Montrons qu’elle est vraie au rang suivant c’est-à-dire $A^{n+1}=PT^{n+1}Q$
$\begin{align*} A^{n+1}&=A^nA\\
&=PT^nQPTQ \\
&=PT^nTQ\\
&=PT^{n+1}Q
\end{align*}$
La propriété est donc vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $1$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ non nul on a $A^n=PT^nQ$.
$\quad$
c. Initialisation : Si $n=1$ on a :
$\begin{pmatrix}0,8&0,5\times 1\times 1\\0&0,8\end{pmatrix}=\begin{pmatrix}0,8&0,5\\0&0,8\end{pmatrix}=T$
La propriété est donc vraie au rang $1$
$\quad$
Hérédité : On suppose que la propriété est vraie au rang $n$ : $T^n=\begin{pmatrix}0,8^n&0,5n\times 0,8^{n-1}\\0&0,8^n\end{pmatrix}$.
Montrons qu’elle est vraie au rang suivant, c’est-à-dire que $T^{n+1}=\begin{pmatrix}0,8^{n+1}&0,5(n+1)\times 0,8^{n}\\0&0,8^{n+1}\end{pmatrix}$
$\begin{align*} T^{n+1}&=T^nT \\
&=\begin{pmatrix}0,8^n&0,5n\times 0,8^{n-1}\\0&0,8^n\end{pmatrix} \times \begin{pmatrix}0,8&0,5\\0&0,8\end{pmatrix} \\
&=\begin{pmatrix} 0,8^{n+1}+0&0,5\times 0,8^{n}+0,5n\times 0,8^n\\0&0,8^{n+1}\end{pmatrix} \\
&=\begin{pmatrix}0,8^{n+1}&0,5\times 0,8^{n}(1+n)\\0&0,8^{n+1}\end{pmatrix}
\end{align*}$
La propriété est donc vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $1$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ non nul on a :$T^n=\begin{pmatrix}0,8^n&0,5n\times 0,8^{n-1}\\0&0,8^n\end{pmatrix}$.
$\quad$ Initialisation : Si $n=1$ on a : - Lucie exécute l'algorithme ci-dessous et obtient en sortie $N = 40$. Quelle conclusion Lucie peut-elle énoncer pour les buses et les campagnols ? $$\begin{array}{|rl|} \hline \text{Initialisation: }& N \text{prend la valeur } 0 \\ & B \text{ prend la valeur 1000} \\ & C \text{ prend la valeur 1500} \\ \text{Traitement :} & \text{Tant que } B > 2 \text{ ou } C > 2 \\ & \qquad N \text{ prend la valeur } N + 1 \\ & \qquad R \text{ prend la valeur }B \\ & \qquad B \text{ prend la valeur } - 0,3R + 0,5C \\ & \qquad C \text{ prend la valeur }- 0,5R + 1,3C \\ &\text{ Fin Tant Que} \\ \text{Sortie :} & \text{Afficher } N \\ \hline \end{array} $$ L’algorithme permet de dire qu’en 2040 le nombre de buses et celui de campagnols seront inférieurs ou égaux à $2$ (ce qui est très bas).
- On admet que, pour tout entier naturel $n$ non nul, on a \[U_n = \begin{pmatrix} 1000 \times 0,8^n +\dfrac{625}2n \times 0,8^n \\[.4cm] 1500 \times 0,8^n + \dfrac{625}2n \times 0,8^n \end{pmatrix} \] et \[n \leqslant 10 \times 1,1^n.\]
- En déduire les limites des suites $\left(b_n\right)$ et $\left(c_n\right)$. Pour tout entier naturel $n$ non nul on a :
- Des mesures effectuées dans des territoires comparables montrent que la population de campagnols reste toujours supérieure à au moins $50$ individus. À la lumière de ces informations, le modèle proposé dans l'exercice vous paraît-il cohérent ? Les mesures effectuées permettent de dire que, pour tout entier naturel $n$ non nul, on a $b_n \geq 50$ et $c_n \geq 50$ ce qui contredit le fait que les limites respectives des suites sont nulles.
$b_n=1~000\times 0,8n+\dfrac{625}{2}n\times 0,8^n$ et $c_n=1~500\times 0,8^n+\dfrac{625}{2}n\times 0,8^n$
On a $-1<0,8<1$ donc $\lim\limits_{n \to +\infty} 0,8^n=0$
On a admis que, pour tout entier naturel $n$ non nul on a :
$n \leq 10 \times 1,1^n \iff n \times 0,8^n \leq 10 \times 0,88^n$
Or $-1<0,88<1$ donc $\lim\limits_{n \to +\infty} 0,88^n=0$
Ainsi $\lim\limits_{n \to +\infty} b_n=0$ et $\lim\limits_{n \to +\infty} c_n=0$
$\quad$
Le modèle proposé ne paraît donc pas cohérent.
$\quad$
$\begin{pmatrix}0,8&0,5\times 1\times 1\\0&0,8\end{pmatrix}=\begin{pmatrix}0,8&0,5\\0&0,8\end{pmatrix}=T$
La propriété est donc vraie au rang $1$
$\quad$
Hérédité : On suppose que la propriété est vraie au rang $n$ : $T^n=\begin{pmatrix}0,8^n&0,5n\times 0,8^{n-1}\\0&0,8^n\end{pmatrix}$.
Montrons qu’elle est vraie au rang suivant, c’est-à-dire que $T^{n+1}=\begin{pmatrix}0,8^{n+1}&0,5(n+1)\times 0,8^{n}\\0&0,8^{n+1}\end{pmatrix}$
$\begin{align*} T^{n+1}&=T^nT \\
&=\begin{pmatrix}0,8^n&0,5n\times 0,8^{n-1}\\0&0,8^n\end{pmatrix} \times \begin{pmatrix}0,8&0,5\\0&0,8\end{pmatrix} \\
&=\begin{pmatrix} 0,8^{n+1}+0&0,5\times 0,8^{n}+0,5n\times 0,8^n\\0&0,8^{n+1}\end{pmatrix} \\
&=\begin{pmatrix}0,8^{n+1}&0,5\times 0,8^{n}(1+n)\\0&0,8^{n+1}\end{pmatrix}
\end{align*}$
La propriété est donc vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $1$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ non nul on a :$T^n=\begin{pmatrix}0,8^n&0,5n\times 0,8^{n-1}\\0&0,8^n\end{pmatrix}$.
$\quad$
$\quad$
- Vues: 49593