Baccalauréat S Antilles Guyane16 juin 2017 - Exercice 3
Exercice 3 5 points
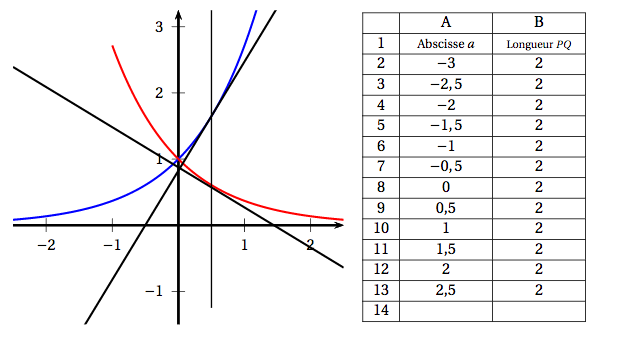
Soient $f$ et $g$ les fonctions définies sur l'ensemble $\mathbb R$ des nombres réels par \[f(x) = \text{e}^x\qquad \text{ et }\qquad g(x) = \text{e}^{- x}.\] On note $\mathcal{C}_f$ la courbe représentative de la fonction $f$ et $\mathcal{C}_g$ celle de la fonction $g$ dans un repère orthonormé du plan. Pour tout réel $a$, on note $M$ le point de $\mathcal{C}_f$ d'abscisse $a$ et $N$ le point de $\mathcal{C}_g$ d'abscisse $a$. La tangente en $M$ à $\mathcal{C}_f$ coupe l'axe des abscisses en $P$, la tangente en $N$ à $\mathcal{C}_g$ coupe l'axe des abscisses en $Q$. À l'aide d'un logiciel de géométrie dynamique, on a représenté la situation pour différentes valeurs de $a$ et on a relevé dans un tableur la longueur du segment $[PQ]$ pour chacune de ces valeurs de $a$.
Les questions 1 et 2 peuvent être traitées de manière indépendante.
- Démontrer que la tangente en $M$ à $\mathcal{C}_f$ est perpendiculaire à la tangente en $N$ à $\mathcal{C}_g$.
-
- Que peut-on conjecturer pour la longueur $PQ$ ?
- Démontrer cette conjecture.
- Vues: 32960
