Baccalauréat S Antilles Guyane 18 juin 2019 - Correction Exercice 1
Correction de l'exercice 1 (6 points)
Partie A
Soit $a$ et $b$ des nombres réels. On considère une fonction $f$ définie sur $[0~;~+\infty[$ par \[f(x) = \dfrac{a}{1 + \text{e}^{-bx}}.\] La courbe $\mathcal{C}_f$ représentant la fonction $f$ dans un repère orthogonal est donnée ci-dessous. La courbe $\mathcal{C}_f$ passe par le point A(O ; 0,5). La tangente à la courbe $\mathcal{C}_f$ au point A passe par le point B(10; 1). 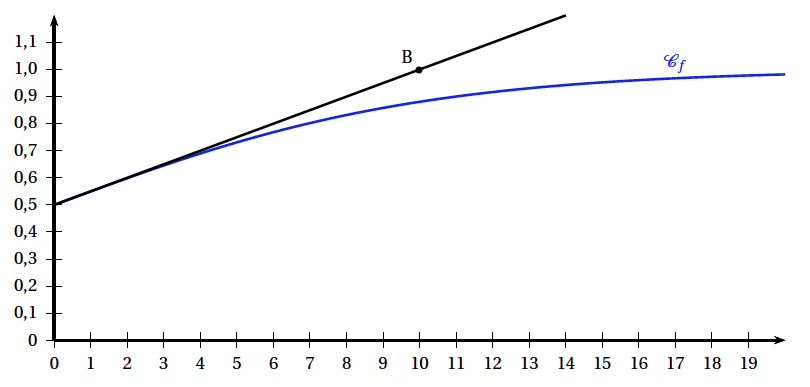
- Justifier que $a = 1$. On obtient alors, pour tout réel $x \geqslant 0$, \[f(x) = \dfrac{1}{1 + \text{e}^{-bx}}.\] Le point $A(0;0,5)$ appartient à la courbe $\mathscr{C}_f$.
- On admet que la fonction $f$ est dérivable sur $[0~;~+\infty[$ et on note $f'$ sa fonction dérivée. Vérifier que, pour tout réel $x \geqslant 0$ \[f'(x) = \dfrac{b\text{e}^{-bx}}{\left(1 + \text{e}^{-bx}\right)^2}.\] Pour tout réel $x\geq 0$ on a $f(x)=\dfrac{1}{1+\text{e}^{-bx}}$
- En utilisant les données de l'énoncé, déterminer $b$. Le coefficient directeur de la tangente à la courbe $C_f$ passe également par le point $B(10;1)$.
Donc
$\begin{align*} f(0)=0,5&\iff \dfrac{a}{1+1} =0,5 \\
&\iff a=1\end{align*}$
$\quad$
Donc :
$\begin{align*} f'(x)&=-\dfrac{-b\text{e}^{-bx}}{\left(1+\text{e}^{-bx}\right)^2 }\\
&=\dfrac{b\text{e}^{-bx}}{\left(1+\text{e}^{-bx}\right)^2 }\end{align*}$
$\quad$
Son coefficient directeur est donc $a=\dfrac{1-0,5}{10-0}=0,05$.
On a également $a=f'(0)$.
Or $f'(0)=\dfrac{b}{(1+1)^2}=\dfrac{b}{4}$
Par conséquent $\dfrac{b}{4}=0,05\iff b=0,2$
$\quad$
Partie B
La proportion d'individus qui possèdent un certain type d'équipement dans une population est modélisée par la fonction $p$ définie sur $[0~;~+\infty[$ par \[p(x) = \dfrac{1}{1 + \text{e}^{-0,2x}}.\] Le réel $x$ représente le temps écoulé, en année, depuis le 1erjanvier 2000. Le nombre $p(x)$ modélise la proportion d'individus équipés après $x$ années. Ainsi, pour ce modèle, $p(0)$ est la proportion d'individus équipés au 1er janvier 2000 et $p(3,5)$ est la proportion d'individus équipés au milieu de l'année 2003.
- Quelle est, pour ce modèle, la proportion d'individus équipés au 1er janvier 2010? On en donnera une valeur arrondie au centième.
-
- Déterminer le sens de variation de la fonction $p$ sur $[0~;~+\infty[$. Au 1er janvier 2010 on a $x=10$
- Calculer la limite de la fonction $p$ en $+\infty$. La fonction $p$ correspond à la fonction $f$ pour $b=0,2$.
- Interpréter cette limite dans le contexte de l'exercice. $\lim\limits_{x\to +\infty} -0,2x=-\infty$ et $\lim\limits_{X \to -\infty} \text{e}^X=0$.
Or $p(10)=\dfrac{1}{1+\text{e}^{-2}}\approx 0,88$.
Ainsi, environ 88% des individus sont équipés au 1er janvier 2010.
$\quad$
La fonction $p$ est donc dérivable sur l’intervalle $[0;+\infty[$ et $p'(x)=\dfrac{\text{e}^{-0,2x}}{\left(1+\text{e}^{-0,2x}\right)^2}$.
La fonction carré est positive et la fonction exponentielle est strictement positive sur $\mathbb R$.
Par conséquent, pour tout réel $x\geq 0$ on a $p'(x)>0$ et la fonction $p$ est strictement croissante sur $[0;+\infty[$.
$\quad$
Donc $\lim\limits_{x \to +\infty} \text{e}^{-0,2x}=0$ et $\lim\limits_{x \to +\infty}p(x)=1$.
$\quad$ - On considère que, lorsque la proportion d'individus équipés dépasse 95 %, le marché est saturé. Déterminer, en expliquant la démarche, l'année au cours de laquelle cela se produit. On veut résoudre l’inéquation
- On définit la proportion moyenne d'individus équipés entre 2008 et 2010 par \[m = \dfrac{1}{2}\displaystyle\int_8^{10} p(x)\:\text{d}x.\]
- Vérifier que, pour tout réel $x \geqslant 0$, \[p(x) = \dfrac{\text{e}^{0,2x}}{1 + \text{e}^{0,2x}}.\] Pour tout réel $x\geq 0$ on a :
- En déduire une primitive de la fonction $p$ sur $[0~;~+\infty[$. Pour tout réel $x$ on a $p(x)=\dfrac{1}{0,2}\times \dfrac{0,2\text{e}^{0,2x}}{1+\text{e}^{0,2x}}$.
- Déterminer la valeur exacte de $m$ et son arrondi au centième. Ainsi :
$\begin{align*} p(x)&=\dfrac{1}{1+\text{e}^{-0,2x}} \\
&=\dfrac{1}{1+\dfrac{1}{\text{e}^{0,2x}}} \\
&=\dfrac{1}{\dfrac{\text{e}^{0,2x}+1}{\text{e}^{0,2x}}} \\
&=\dfrac{\text{e}^{0,2x}}{1+\text{e}^{0,2x}}\end{align*}$
$\quad$
On a donc une expression de la forme $\dfrac{u’}{u}$.
Une primitive de la fonction $p$ sur cet intervalle est donc la fonction $P$ définie sur l’intervalle $[0;+\infty[$ par $P(x)=\dfrac{\ln\left(1+\text{e}^{0,2x}\right)}{0,2}$.
$\quad$
$\begin{align*} m&=\displaystyle \dfrac{1}{2}\int_8^{10}p(x)\text{d}x \\
&=\dfrac{1}{2}\left(P(10)-P(8)\right)\\
&=\dfrac{1}{2}\times \dfrac{1}{0,2}\left(\ln\left(1+\text{e}^{2}\right)-\ln\left(1+\text{e}^{1,6}\right)\right)\\
&=\dfrac{1}{0,4}\ln\dfrac{1+\text{e}^{2}}{1+\text{e}^{1,6}}\\
&\approx 0,86\end{align*}$
$\quad$
$\begin{align*} p(x)>0,95 &\iff \dfrac{1}{1+\text{e}^{-0,2x}}>0,95 \\
&\iff 1+\text{e}^{-0,2x}<\dfrac{1}{0,95} \\
&\iff \text{e}^{-0,2x}<\dfrac{0,05}{0,95} \\
&\iff -0,2x<\ln \dfrac{1}{19} \\
&\iff x>-5\ln \dfrac{1}{19}\end{align*}$
Or $-5\ln \dfrac{1}{19} \approx 14,72$.
C’est au cours de l’année 2014, entre août et septembre, que le marché sera saturé.
$\quad$
- Vues: 80250
