Baccalauréat STI2D NOUVELLE CALÉDONIE Mars 2014 2013 - Correction Exercice 4
Exercice 4 7 points
Dans tout l'exercice, on désigne par $\mathbb R$ l'ensemble des nombres réels.
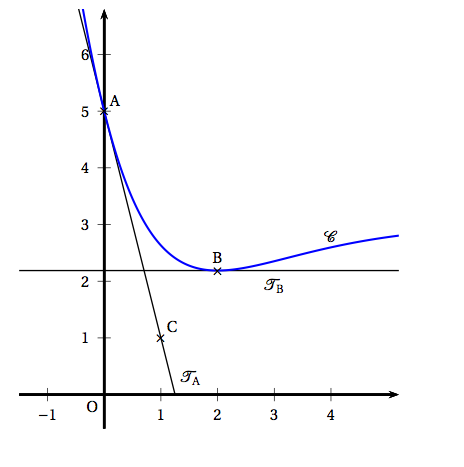
On donne ci-dessous une petite partie de la courbe représentative $\mathcal{C}$ d'une fonction $f$ définie et dérivable sur $\mathbb R$, dans un repère orthonormé du plan. On note $f'$ la fonction dérivée de $f$. La courbe $\mathcal{C}$ passe par le point $A (0 ; 5)$ et par le point $B$ d'abscisse 2. La tangente $T_A$ à la courbe au point $A$ passe par le point $C(1 ; 1)$ et la tangente $T_B$ au point $B$ est horizontale.
Partie A
Dans ce questionnaire à choix multiples, aucune justification n'est demandée. Pour chacune des questions, une seule des réponses proposées est correcte.
Une bonne réponse rapporte $0,5$ point.
Une mauvaise réponse ou l'absence de réponses n'enlève ni ne rapporte aucun point. On notera sur la copie le numéro de la question et la réponse choisie.
- La valeur de $f(0)$ est :
- $- 4$
- $4$
- $1,2$
- autre réponse
La courbe $\mathcal{C}$ passe par le point $A(0;5)$ donc $f(0)=5$
- La valeur de $f'(0)$ est :
- $- 4$
- $4$
- $1,2$
- autre réponse
Le nombre dérivé $f'(0)$ est égal au coefficient directeur de la tangente $T_A$ à la courbe au point $A(0;5)$ or cette tangente passe également par le point $C(1;1)$ d'où $f'(0)=\dfrac{y_C-y_A}{x_C-x_A}$ . Soit $f'(0)=\dfrac{1-5}{1-0}=-4$
- La valeur de $f'(2)$ est :
- $0$
- $2,1$
- $3 $
- autre réponse
La tangente $T_B$ à la courbe au point $B$ d'abscisse 2 est parallèle à l'axe des abscisses donc $f'(2)=0;$
- Un encadrement de $\displaystyle\int_{0}^2 f(x) \, dx$ par des entiers naturels est :
- $3 \leqslant \displaystyle\int_{0}^2 f(x) \, dx \leqslant 4$
- $5 \leqslant \displaystyle\int_{0}^2 f(x) \, dx \leqslant 7$
- $2 \leqslant \displaystyle\int_{0}^2 f(x) \, dx \leqslant 5$
- $0 \leqslant \displaystyle\int_{0}^2 f(x) \, dx \leqslant 2$
L'intégrale $\displaystyle\int_{0}^2 f(x) \, d x$ est égale à l'aire, exprimée en unités d'aire, du domaine limité par la courbe $\mathcal{C}$ l'axe des abscisses et les droites d'équations $x=0$ et $x=2$. Or cette aire est visiblement supérieure à 5 unités d'aire. $5 \leqslant \displaystyle\int_{0}^2 f(x) \,d x \leqslant 7$
Partie B
La fonction $f$ représentée dans la PARTIE A est définie sur $\mathbb R$ par $f(x) = \left(- x^2 - 2x + 2\right)e^{- x} + 3$.
- On admet que la limite de la fonction $f$ en $+ \infty$ est 3. Déterminer la limite de $f$ en $- \infty$.
- On désigne par $f'$ la fonction dérivée de la fonction $f$ et on admet que pour tout nombre réel $x$ appartenant à $\mathbb R$, $f'(x) = \left(x^2 - 4\right)e^{- x}$.
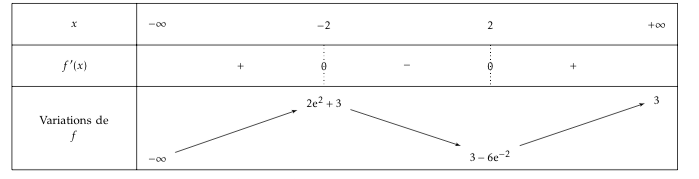
- Étudier le signe de $f'(x)$ suivant les valeurs de $x$. La fonction exponentielle étant strictement positive sur $\mathbb R$, on déduit que pour tout réel $x ; e^{- x}>0$, et ainsi $f'(x)$ a le signe de $x^2-4$ $x^2-4$ est un trinôme du second degré qui a pour racines $-2$ et $2$; il a donc le signe de $a=1$ à l'extérieur des racines et celui de $-a$ à l'intérieur.
- En déduire le tableau de variation de la fonction $f$.

- On considère la fonction $F$ définie sur $\mathbb R$ par $F(x) = \left(x^2 + 4x + 2\right)e^{- x} + 3x$. Vérifier que la fonction $F$ est une primitive de la fonction $f$ sur $\mathbb R$. Ici $F(x) = \left(x^2 + 4x + 2\right)e^{- x} + 3x$ est du type $F=u+v$, ainsi $F' =u'+v'$.
- On considère le domaine $\mathcal{D}$ du plan limité par la courbe $\mathcal{C}$ l'axe des abscisses et les droites d'équations $x = 0$ et $x = 2$.
- Calculer la valeur exacte de l'aire $\mathcal{A}$, exprimée en unités d'aire, du domaine $\mathcal{D}$. Sur l'intervalle $[0;2]$ la fonction $f$ est strictement décroissante et $f(2)=3-6 e^{-2} \approx 2,19$ donc $f$ est positive sur l'intervalle $[0;2]$.
- Donner une valeur approchée de $\mathcal{A}$ au centième.
Par conséquent, l'aire $\mathcal{A}$, exprimée en unités d'aire, du domaine $\mathcal{D}$ est égale à l'intégrale de la fonction $f$ sur l'intervalle $[0;2]$ :
$\displaystyle\int_{0}^2 f(x) \,d x =F(2)-F(0)$.
$F(2)-F(0)= 14 e^{-2} + 6-2=14 e^{-2} +4$$\mathcal{A}=14 e^{-2} +4$ unités d'aire.$\mathcal{A}\approx 5,89$ unités d'aire.
Au voisinage de $-\infty$ , une fonction polynôme à la même limite que son monôme de plus haut degré.
$ \lim\limits_{x \to -\infty}- x^2 - 2x + 2= \lim\limits_{x \to -\infty}- x^2 =-\infty$
$\left.\begin{array}{l} \lim\limits_{x \to -\infty}\left(- x^2 - 2x + 2\right)e^{- x}=-\infty\\ \lim\limits_{x \to -\infty}~3=3 \end{array}\right\}$ par somme on obtient: $\lim\limits_{x \to -\infty}~f(x)= -\infty$
où $u(x)= \left(x^2 + 4x + 2\right)e^{- x} $ , donc $u=ab$ d'où $u'=a'b+b'a$.
$a(x)= \left(x^2 + 4x + 2\right)$ et $b(x)=e^{- x}$
Alors $a'(x)= \left(2x+4\right)$ et $b'(x)=-e^{- x}$
Puis $u'(x)=\left(2x+4\right) e^{- x}+ \left(-e^{- x}\right)\left(x^2 + 4x + 2\right)=e^{- x}\left(2x+4 -x^2 - 4x - 2\right)=e^{- x}\left( -x^2 - 2x+ 2\right)$ et $v'(x)=3$, et donc $F'(x)=u'(x)+v'(x)=e^{- x}\left( -x^2 - 2x+ 2\right)+3=f(x)$
- Vues: 19213
