Baccalauréat S Antilles-Guyane 20 juin 2016 - Correction Exercice 3
Page 6 sur 10
Correction de l'exercice 3 (5 points)
Partie A
On considère la fonction $f$ définie pour tout réel $x$ par $f(x)=x\text{e}^ {1-x^2}$.
- Calculer la limite de la fonction $f$ en $+\infty$.
Indication: on pourra utiliser que pour tout réel $x$ différent de $0$, $f(x)=\frac{\text{e}}{x}\times\frac{x^2}{\text{e}^ {x^2}}$.
On admettra que la limite de la fonction $f$ en $-\infty$ est égale à 0. - $f(x)=x\text{e}^{1-x^2}=x\text{e}\times \dfrac{1}{\text{e}^{x^2}}=\dfrac{\text{e}}{x}\times \dfrac{x^2}{\text{e}^{x^2}}$
$\lim\limits_{x \to +\infty} x^2=+\infty$ et $\lim\limits_{X \to +\infty} \dfrac{\text{e}^X}{X}=+\infty$ par conséquent $\lim\limits_{X \to +\infty} \dfrac{X}{\text{e}^X}=0$
Donc $\lim\limits_{x \to +\infty} \dfrac{x^2}{\text{e}^{x^2}}=0$.
De plus $\lim\limits_{x \to +\infty} \dfrac{\text{e}}{x}=0$.
Donc $\lim\limits_{x \to +\infty} f(x)=0$
$\quad$- On admet que $f$ est dérivable sur $\mathbb R$ et on note $f'$ sa dérivée.
Démontrer que pour tout réel $x$, \[ f'(x)=\left(1-2x^2\right)\text{e}^ {1-x^2}. \] $\begin{align*} f'(x)&=\text{e}^{1-x^2}+x\times (-2x)\text{e}^{1-x^2} \\ - En déduire le tableau de variations de la fonction $f$. La fonction exponentielle est strictement positive. Le signe de $f'(x)$ ne dépend donc que de celui de $1-2x^2$.
&=\left(1-2x^2\right)\text{e}^{1-x^2}
\end{align*}$
$\quad$
$1-2 x^2 $ est un trinôme du second degré qui a pour racines $-\frac{\sqrt 2}{2}$ et $\frac{\sqrt 2}{2}$; il a donc le signe de $a=-2$ à l'extérieur des racines et celui de $-a$ à l'intérieur.et $1-2x^2>0 \iff \dfrac{1}{2}>x^2 \iff x \in \left[-\dfrac{\sqrt{2}}{2};\dfrac{\sqrt{2}}{2}\right]$
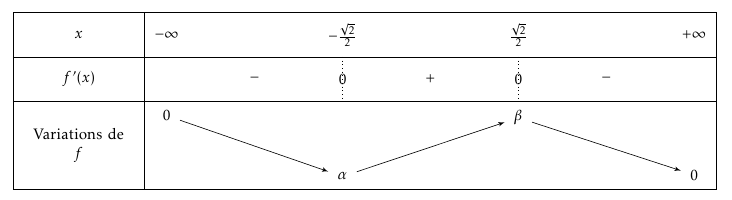
On obtient ainsi le tableau de variations suivant :
où $\alpha=f\left(-\dfrac{\sqrt{2}}{2}\right)=-\dfrac{\sqrt{2}}{2}\text{e}^{0,5}$ et $\beta =f\left(-\dfrac{\sqrt{2}}{2}\right)=\dfrac{\sqrt{2}}{2}\text{e}^{0,5}$ - On admet que $f$ est dérivable sur $\mathbb R$ et on note $f'$ sa dérivée.
Partie B
On considère la fonction $g$ définie pour tout réel $x$ par $g(x)=\text{e}^ {1-x}$.
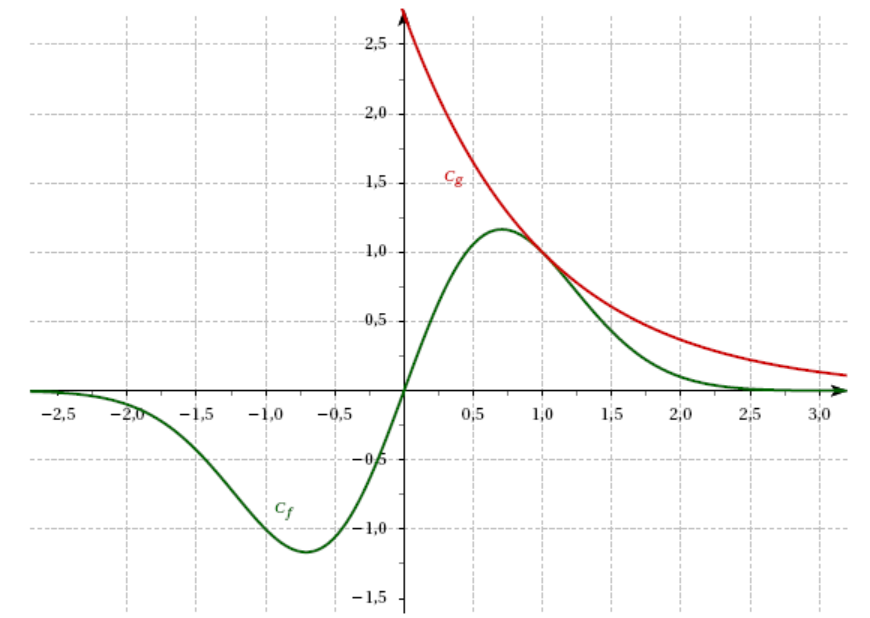
Sur le graphique ci-dessous, on a tracé dans un repère les courbes représentatives $\mathcal{C}_f$ et $\mathcal{C}_g$ respectivement des fonctions $f$ et $g$.
Le but de cette partie est d'étudier la position relative de ces deux courbes.
- Après observation du graphique, quelle conjecture peut-on émettre ? Il semblerait que $\mathscr{C}_g$ soit toujours au-dessus de $\mathscr{C}_f$.
- Justifier que, pour tout réel $x$ appartenant à $]-\infty~;~0]$, $f(x)<g(x)$. Pour tout $x\in]-\infty;0]$, $f(x) \leqslant 0$ et $g(x)>0$.
- Dans cette question, on se place dans l'intervalle $]0~;~+\infty[$.
On pose, pour tout réel $x$ strictement positif, $\Phi(x)=\ln x-x^2+x$.- Montrer que, pour tout réel $x$ strictement positif, \[ f(x)\leqslant g(x)\text{ équivaut à }\Phi(x)\leqslant 0. \] On admet pour la suite que $f(x)=g(x)$ équivaut à $\Phi(x)=0$. Pour tout $x\in]-\infty;0]$, $f(x) \leqslant 0$ et $g(x)>0$.
- On admet que la fonction $\Phi$ est dérivable sur $]0~;~+\infty[$. Dresser le tableau de variation de la fonction $\Phi$. (Les limites en $0$ et $+\infty$ ne sont pas attendues.)
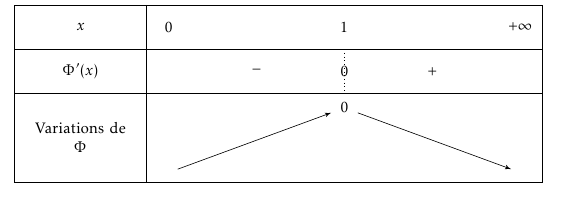
- En déduire que, pour tout réel $x$ strictement positif, $\Phi(x)\leqslant 0$. D’après le tableau de variations, pour tout réel $x >0$ on a $\Phi(x) \leqslant 0$.En effet $\Phi$ présente un maximum en $1$ qui vaut $0$
Donc sur cet intervalle $f(x)< g(x)$.
$\quad$
$\begin{align*} f(x) \leqslant g(x) &\iff x\text{e}^{1-x^2}\leqslant \text{e}^{1-x} \\
&\iff x \leqslant \dfrac{\text{e}^{1-x}}{\text{e}^{1-x^2}} \\
&\iff x \leqslant \text{e}^{x^2-x} \\
&\iff \ln x \leqslant x^2-x \\
&\iff \Phi(x) \leqslant 0
\end{align*}$
$\quad$
b. $\Phi'(x)=\dfrac{1}{x}-2x+1 = \dfrac{-2x^2+x+1}{x}$
Pour tout $x\in ]0;+\infty[$, le signe de $\Phi'(x)$ ne dépend que de celui de $-2x^2+x+1$
$\Delta = 1^2-4\times (-2)=9 >0$
$-2 x^2+x+1$ est un trinôme du second degré qui a pour racines $-\frac{1}{2}$ et $1$; il a donc le signe de $a=-2$ à l'extérieur des racines et celui de $-a$ à l'intérieur.
On obtient donc le tableau de variations suivant :
$\quad$ -
- La conjecture émise à la question 1. de la partie B est-elle valide ? D’après la question 3.a. pour tout réel $x$ strictement positif, $f(x) \leqslant g(x) \iff \Phi(x) \leqslant 0$.
- Montrer que $\mathcal{C}_f$ et $\mathcal{C}_g$ ont un unique point commun, noté $A$. Sur $]-\infty;0]$, $f(x) < g(x)$ : les deux courbes n’ont pas de point commun sur cet intervalle.
- Montrer qu'en ce point $A$, ces deux courbes ont la même tangente. $f'(1)=(1-2)\text{e}^0=-1$ et $g'(1)=-\text{e}^0=-1$
Ainsi, $\mathscr{C}_f$ est bien toujours en dessous de $\mathscr{C}_g$ sur $]0;+\infty[$.
On a prouvé que pour tout $x \leqslant 0$, $f(x)\leqslant g(x)$.
Donc $\mathscr{C}_f$ est bien toujours en dessous de $\mathscr{C}_g$ sur $]-\infty;0]$.
La conjecture de la question 1. est donc valide.
$\quad$
Sur $]0;+\infty[$, $f(x)=g(x) \iff \Phi(x)=0 \iff x=1$
$\mathscr{C}_g$ et $\mathscr{C}_f$ ont donc un unique point commun : le point $A$ d’abscisse $1$.
$g(1)=\text{e}^0=1$.
$\quad$
Les deux tangentes en $A$ ont donc le même coefficient directeur. Puisqu’elles passent par le point $A$ cela signifie donc qu’elles sont confondues.
$\quad$
$\quad$
Donc sur cet intervalle $f(x)< g(x)$.
$\quad$
Partie C
- Trouver une primitive $F$ de la fonction $f$ sur $\mathbb R$. Une primitive de $f$ sur $\mathbb R$ est la fonction $F$ définie sur $\mathbb R$ par $F(x)=-\dfrac{1}{2}\text{e}^{1-x^2}$
- En déduire la valeur de $\displaystyle\int_0^1\left(\text{e}^ {1-x}-x\text{e}^ {1-x^2}\right)\text{d}x$. $\begin{align*} \displaystyle \int_0^1\left(\text{e}^{1-x}-x\text{e}^{1-x^2}\right)\mathrm{d}x &= \big[-\text{e}^{1-x}-F(x)\big]_0^1 \\
- Interpréter graphiquement ce résultat. Ce résultat correspond à l’aire du domaine compris entre $\mathscr{C}_g$, $\mathscr{C}_f$ et les droites d’équation $x=0$ et $x=1$.
$\quad$
&=-1+\dfrac{1}{2}-\left(-\text{e}+\dfrac{1}{2}\text{e}\right) \\
&=\dfrac{1}{2}\left(\text{e}-1\right)
\end{align*}$
$\quad$
$\quad$
- Vues: 34071