Baccalauréat S Antilles-Guyane 20 juin 2016 - Exercice 4
Page 7 sur 10
Exercice 4 5 points
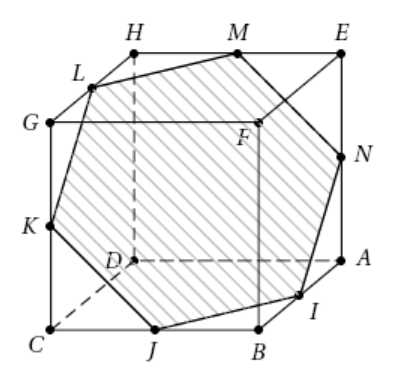
$ABCDEFGH$ est un cube d'arête égale à 1.
L'espace est muni du repère orthonormé $(D~;\vec{DC},\vec{DA},\vec{DH})$.
Dans ce repère, on a:
$D(0~;~0~;~0)$, $C(1~;~0~;~0)$, $A(0~;~1~;~0)$,
$H(0~;~0~;~1)$ et $E(0~;~1~;~1)$.
Soit $I$ le milieu de $[AB]$.
Soit $\mathcal{P}$ le plan parallèle au plan $(BGE)$ et passant par le point $I$.
On admet que la section du cube par le plan $\mathcal{P}$ représentée ci-dessus est un hexagone dont les sommets $I$, $J$, $K$, $L$, $M$, et $N$ appartiennent respectivement aux arêtes $[AB]$, $[BC]$, $[CG]$, $[GH]$, $[HE]$ et $[AE]$.
-
- Montrer que le vecteur $\vec{DF}$ est normal au plan $(BGE)$.
- En déduire une équation cartésienne du plan $\mathcal{P}$.
- Montrer que le point $N$ est le milieu du segment $[AE]$.
-
- Déterminer une représentation paramétrique de la droite $(HB)$.
- En déduire que la droite $(HB)$ et le plan $\mathcal{P}$ son sécants en un point $T$ dont on précisera les coordonnées.
- Calculer, en unités de volume, le volume du tétraèdre $FBGE$.
- Vues: 24818