Baccalauréat S Liban 5 juin 2017 - Exercice 3
Page 5 sur 10
Exercice 3 3 points
Soit $k$ un réel strictement positif. On considère les fonctions $f_k$ définies sur $\mathbb R$ par : \[f_k(x) = x + k\text{e}^{- x}.\] On note $\mathcal{C}_k$ la courbe représentative de la fonction $f_k$ dans un plan muni d'un repère orthonormé. On a représenté ci-dessous quelques courbes $\mathcal{C}_k$ pour différentes valeurs de $k$. 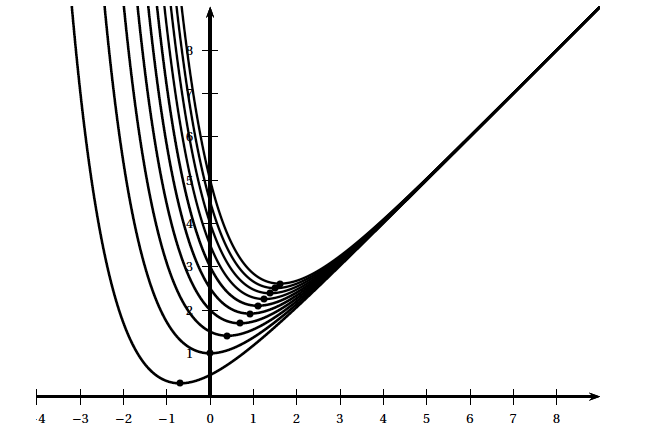
Pour tout réel $k$ strictement positif, la fonction $f_k$ admet un minimum sur $\mathbb R$. La valeur en laquelle ce minimum est atteint est l'abscisse du point noté $A_k$ de la courbe $\mathcal{C}_k$. il semblerait que, pour tout réel $k$ strictement positif, les points $A_k$ soient alignés. Est-ce le cas ?
- Vues: 34636
