Rédigé par Luc Giraud le 20 juillet 2019. Publié dans Cours en TS.

Limites - Limites et opérations

Page 3 sur 5: Limites et opérations

Page 3 sur 5

Opérations sur les limites

Dans les théorèmes admis ci-dessous, présentés sous forme de tableaux,$u$ et $v$ sont des fonctions définies sur un même intervalle $I$ et $\bigcirc$ désigne $+\infty ,-\infty$ ou un nombre réel $a$; $L$ et $L'$ sont des nombres réels.

somme

Comment déterminer $\displaystyle\lim_{x \to \bigcirc}[u(x)+v(x)]$? $$\begin{array}{ |c|c|c|c|c|c|c| } \hline \text{ Si } \displaystyle\lim_{x \to \bigcirc}u(x)& L\in \mathbb{R} & L & L & +\infty & +\infty & -\infty \\ \hline \text{ et } \displaystyle\lim_{x \to \bigcirc} v(x) & L'\in \mathbb{R} & +\infty & -\infty & +\infty & -\infty & -\infty \\ \hline \text{ alors }\displaystyle\lim_{x \to \bigcirc}[u(x)+v(x)] & L+L' & +\infty & -\infty & +\infty & ? & -\infty \\ \hline \end{array} $$ Les points d'interrogation ( ?) signalent les cas indéterminés. Ce sont des cas pour lesquels une étude spécifique doit être menée pour déterminer une éventuelle limite.

Cas du produit d'une fonction par une constante

On suppose que la constante $k$ n'est pas nulle. Comment déterminer $\displaystyle\lim_{x \to \bigcirc}[ku(x) ]$?

$$\begin{array}{ |c|c|c|c|c|c| } \hline \text{ Si }\displaystyle\lim_{x \to \bigcirc}u(x) & L\in \mathbb{R} & +\infty & +\infty & -\infty & -\infty \\ \hline \text{ alors } \displaystyle\lim_{x \to \bigcirc} [ku(x)] & kL & +\infty \text{ si } k>0 & -\infty \text{ si } k < 0 & -\infty \text{ si } k > 0 & +\infty \text{ si } k < 0 \\ \hline \end{array} $$

Cas du produit de deux fonctions

Comment déterminer $\displaystyle\lim_{x \to \bigcirc}[u(x)\times v(x) ]$? $$\begin{array}{ |c|c|c|c|c|c| } \hline \text{ Si } \displaystyle\lim_{x \to \bigcirc}u(x)& L\in \mathbb{R} & L\neq 0 & 0 & +\infty \text{ ou } -\infty \\ \hline et \displaystyle\lim_{x \to \bigcirc} v(x) & L' & +\infty \text{ ou } -\infty& +\infty \text{ ou } -\infty& +\infty \text{ ou } -\infty \\ \hline alors \displaystyle\lim_{x \to \bigcirc} [u(x)\times v(x)] & LL' & \pm\infty & \textbf{?} & \pm\infty \\ \hline \end{array}$$ $ \pm \infty$ correspond soit à $+\infty$, soit à $-\infty$. Le signe + ou - s'obtient de façon évidente dans chaque exemple.

Cas de l'inverse :

Comment déterminer $\displaystyle\lim_{x \to \bigcirc} \dfrac{1}{u(x)} $?
$$ \begin{array}{ |c|c|c|c|c| } \hline \text { Si } \displaystyle\lim_{x \to \bigcirc}u(x)& L\neq 0 & 0 & +\infty \text{ ou } -\infty \\ \hline alors \displaystyle\lim_{x \to \bigcirc} \dfrac{1}{u(x)} & \dfrac{1}{L} &\text{ voir le théorème ci dessous } & 0 \\ \hline \end{array} $$

Si $\displaystyle\lim_{x \to \bigcirc}u(x)=0$ et si au voisinage de $\bigcirc$ on a $u(x)>0$, alors on a $\displaystyle\lim_{x \to \bigcirc} \dfrac{1}{u(x)} =+\infty$
Si $\displaystyle\lim_{x \to \bigcirc}u(x)=0$ et si au voisinage de $\bigcirc$ on a $u(x)<0$, alors on a $\displaystyle\lim_{x \to \bigcirc} \dfrac{1}{u(x)} =-\infty$

Cas du quotient :

Sur tout intervalle où le quotient $\dfrac{u(x)}{v(x)}$ est défini, on remarque que $\dfrac{u(x)}{v(x)}=u(x)\times \dfrac{1}{v(x)}$ et on utilise les théorèmes de l'inverse $\dfrac{1}{v(x)}$ et la limite d'un produit.

Limite d'une fonction composée

Soit $g$ et $h$ deux fonctions telles que: $$x\stackrel{g}{ \mapsto}y\stackrel{h}{ \mapsto}z=h(y)=h(g(x))=h \circ g(x)$$ Si $\displaystyle\lim_{x \to a}g(x)=b$ et si $\displaystyle\lim_{y \to b}h(y)=c$, alors $\displaystyle\lim_{x \to a}h(g(x))=c$

Un exemple ?
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=\sqrt{3x^2+5}$. Cherchons $\displaystyle\lim_{x \to-\infty}f(x)$.

On a $\displaystyle\lim_{x \to-\infty}3x^2+5=+\infty$ et $\displaystyle\lim_{y \to +\infty}\sqrt{y}=+\infty$ donc par composée: $\displaystyle\lim_{x\to-\infty}\sqrt{3x^2+5}=+\infty$

Limites et ordre

Compatibilité avec l'ordre : Soit $a$ un réel, $+\infty$ ou $-\infty$. Soit $f$ et $g$ deux fonctions telles que $\lim\limits_{x \to a}f(x)=l$ et $\lim\limits_{x \to a}g(x)=l'$.
Si $f(x)< g(x)$ alors $l \leq l'$

Théorème des gendarmes: Soit trois fonctions $f$, $g$ et $h$ telles que $f(x)\leq g(x) \leq h(x)$ au voisinage de $a$ (réel ou $\pm\infty$). Si les fonctions $f$ et $h$ ont la m\^eme \emph{limite finie} $l$ au voisinage de $a$, alors $g$ a pour limite $l$ au voisinage de $a$.

À connaître On démontre ce théorème dans le cas particulier de $+\infty$ .
Soit $I$ un intervalle ouvert contenant $l$, on doit montrer que $I$ contient tous les réels $g(x)$ pour $x$ assez grand. Par hypothèse,

$\lim\limits_{x \to +\infty}f(x)=l$ donc $I$ contient tous les réels $f(x)$ pour $x$ assez grand, plus précisément, il existe un réel $A$ tel que si $x>A$ alors $f(x)\in I$.
$\lim\limits_{x \to +\infty}h(x)=l$ donc $I$ contient tous les réels $h(x)$ pour $x$ assez grand, plus précisément, il existe un réel $B$ tel que si $x>B$ alors $h(x)\in I$.

Posons $N=\text{max}(A;B)$ alors pour $x>N$, on a $f(x)\in I$ et $h(x)\in I$.\par Dire que $f(x)\leq g(x) \leq h(x)$ au voisinage de $+\infty$, signifie qu'il existe un réel $C$ tel que pour $x>C$, on a $f(x)\leq g(x) \leq h(x)$.

Posons $M=\text{max}(N;C)$ alors pour $x>M$, on a $f(x)\in I$, $h(x)\in I$ et $f(x)\leq g(x) \leq h(x)$.

On en déduit que pour $x>M$, on a $g(x)\in I$; c'est-à-dire que $I$ contient les réels $g(x)$ pour $x$ assez grand.

Soit $f$ la fonction définie sur $\mathbb{R}^*$ par $f(x)=x\sin\left(\dfrac{1}{x}\right)$.\par Pour tout $x>0$, on a $-x\leq f(x) \leq x$

Comme $\displaystyle{\lim_{x \to 0^+}x= \lim_{x \to 0^+}(-x)=0}$, on en déduit que $\displaystyle\lim_{x \to 0^+}f(x)=0$.

De même pour $x<0$, on obtient $\displaystyle\lim_{x \to 0^-}f(x)=0$.

Donc $\displaystyle\lim_{x \to 0}f(x)=0$.

Corollaire du théorème des gendarmes
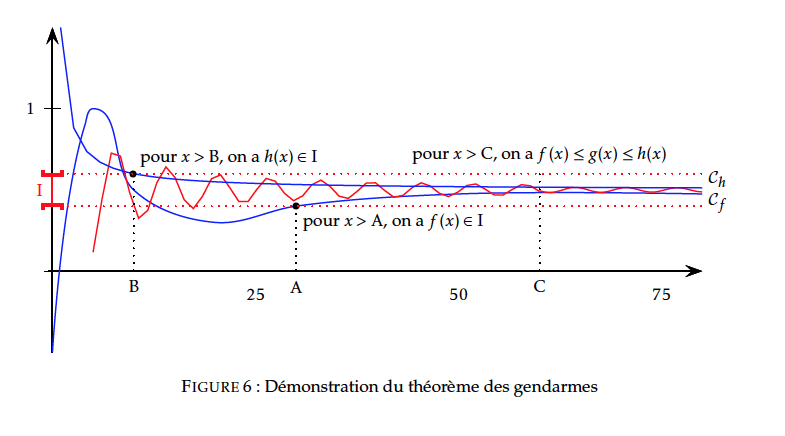
Soit deux fonctions $f$ et $g$ telles que $f\leq g $ au voisinage de $a$ (réel ou $\pm\infty$),

si $\lim\limits_{x\to a}f(x)=+\infty$ alors $\lim\limits_{x\to a}g(x)=+\infty$;
si $\lim\limits_{x\to a}g(x)=-\infty$ alors $\lim\limits_{x\to a}f(x)=-\infty$.

Vues: 12279

Imprimer