Lois normales - Théorème de Moivre - Laplace
Page 2 sur 7
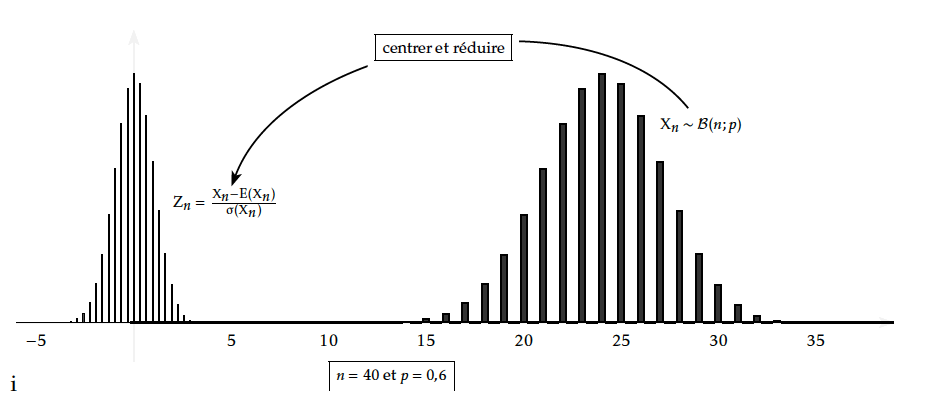
Observation du diagramme associé à la variable aléatoire $Y_n=X_n-np$
Consulter le fichier binomiale n p .ggb
Rappels de 1 S $a$ et $b$ étant des réels fixés, $X$ désignant une variable aléatoire,
- $E(aX+b)=aE(X)$
- $V(a.X+b)=a^2V(X)$
$E(Y_n)=E(1.X_n+\left (-np\right ))=1.E(X_n)+\left (-np\right )=np-np=0$
$V(Y_n)=1^2V(X_n)=V(X_n)=npq$.
$Y_n$ est dite centrée.
La deuxième opération à effectuer semble être de « réduire »l'étalement de $Y_n$ autour de 0.
Observation du diagramme associé à la variable aléatoire $Z_n=\dfrac{Y_n}{\sqrt{npq}}=\dfrac{X_n-np}{\sqrt{npq}}$
$E(Z_n)=\dfrac{1}{\sqrt{npq}}E(Y_n)=0$.\\ $V(Z_n)=\left (\dfrac{1}{\sqrt{npq}}\right )^2V(Y_n)=\dfrac{1}{npq}\times npq=1$.
$Z_n$ est dite centrée et réduite.
Consulter le fichier centrer et réduire une binomiale.ggb
Conjecture
Après avoir remplacé $Z_n$ par une loi continue dont la fonction densité est une fonction en escalier, on observe que cette dernière loi peut être elle-même approchée par une loi continue appelée loi normale $\mathcal{N}(0;1)$.
Théorème de Moivre-Laplace (admis)
Soit $p\in]0;1[$. Pour tout entier $n\geq 1$, soit $X_n\sim\mathcal B(n;p)$ et la variable aléatoire centrée réduite $Z_n=\dfrac{X_n-np}{\sqrt{npq}} $ correspondante .
Alors $Z_n$ converge en loi vers la variable aléatoire $X$ qui suit la loi $\mathcal{N}(0;1)$.
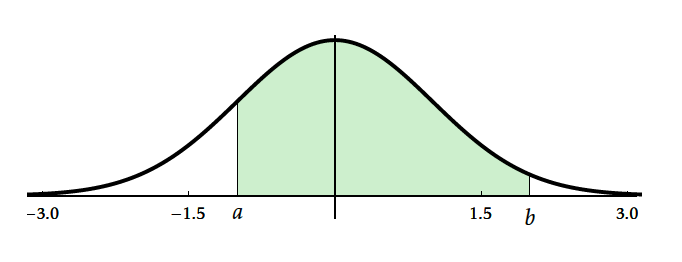
Autrement dit quels que soient $a$ et $b$ deux réels, $a\leq b$. On a \[ \displaystyle\lim_{n\to+\infty} P(a\leq Z_n \leq b)=P(a\leq X\leq b)=\displaystyle\int_a^bf(x)\;dx \quad\text{où}\quad f(x)=\dfrac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2} } \text{ pour tout } x \in \mathbb{R} \]
Alors $Z_n$ converge en loi vers la variable aléatoire $X$ qui suit la loi $\mathcal{N}(0;1)$.
Autrement dit quels que soient $a$ et $b$ deux réels, $a\leq b$. On a \[ \displaystyle\lim_{n\to+\infty} P(a\leq Z_n \leq b)=P(a\leq X\leq b)=\displaystyle\int_a^bf(x)\;dx \quad\text{où}\quad f(x)=\dfrac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2} } \text{ pour tout } x \in \mathbb{R} \]
Ce théorème signifie que, pourvu que $n$ soit suffisamment grand, on peut estimer $P(a\leq Z_n\leq b)$ par $P(a\leq X\leq b)$.
</>Il est admis, voir le TP 8 pour une approche empirique.
</>Il est admis, voir le TP 8 pour une approche empirique.
La loi $\mathcal{N}(0;1)$
- Sur $\mathbb{R} : f(x)=\dfrac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2} }$
- Sur $\mathbb{R} : f(-x)=f(x)$ donc $\mathcal{C}_f$ est symétrique par rapport à l'axe $(O;\vec{j})$
- $f(0)=\dfrac{1}{\sqrt{2\pi}}\approx 0,339$
- On admet $\displaystyle\lim_{b\to +\infty}\int_0^b f(x) \;dx=0,5$; on note $\displaystyle \int_0^{+\infty} f(x) \;dx=0,5$
- On admet $\displaystyle\lim_{a\to -\infty}\int_a^0 f(x) \;dx=0,5$; on note $\displaystyle \int_{-\infty}^0 f(x) \;dx=0,5$
- On admet $\displaystyle\lim_{a\to -\infty\\b\to +\infty}\int_a^b f(x) \;dx=1$; on note $\displaystyle \int_{-\infty}^{+\infty} f(x) \;dx=1$
La seule connaissance de $F(t)=P(X\leq t)$ pour tout $t\in \mathbb{R}$ suffit pour déterminer $P(X\in I)$ pour n'importe quel intervalle de $\mathbb{R}$.
Ici $F$ est appelée $\Pi$. On admet que pour tout $t\in \mathbb{R}$ :
- $ \Pi (t) = P \big( T \leq t\big) = \displaystyle\int _{-\infty }^t f (x) \, {\rm d}x$
- $ \Pi (t) = P \big( T \leq t\big) =0,5+\displaystyle\int _{0 }^t f (x) \, {\rm d}x \qquad \qquad $ même si $t$ est négatif.
- $\Pi(t)$ est l'aire du domaine hachuré ci-dessous.
- Pour obtenir $\Pi(t)$ on utilisait autrefois une table; aujourd'hui on utilise la calculatrice : 0,5+normalFRép(0,t) ( même si $t$ est négatif.)
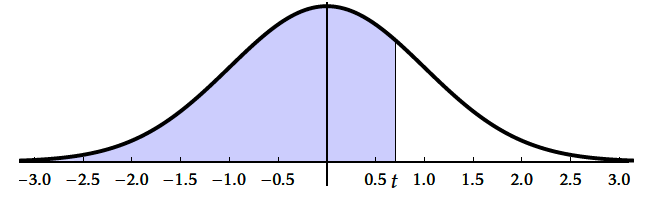
Table de $pi(t)$
- Vues: 22988
