Lois normales - Algorithmes
Algorithme : méthodes de Monte-Carlo
Le but de ces méthodes est de calculer des intégrales par des méthodes probabilistes.
Ces méthodes fonctionnent également pour des fonctions discontinues, ce qui explique son intérêt.
Pour simplifier, on calcule des intégrales de fonctions positives sur l'intervalle $[0;1]$ uniquement.
Méthode du rejet
On suppose qu'on connaît un majorant $M$ d'une fonction $f$ sur l'intervalle $[0;1]$.
Comme $\displaystyle\int_0^1 f(x)dx$ est l'aire du domaine $D=\left\{x\in[0;1], y\in[0;M],y\leq f(x)\right\}$, on tire aléatoirement un grand nombre de points dans le rectangle $[0;1]\times[0;M]$ (les coordonnées suivants des lois uniformes).
On fait ensuite le quotient entre les points situés dans $D$ et le nombre total de points. On obtient ainsi une approximation de $\displaystyle\int_0^1 f(x)dx$.
Programmer et tester cette méthode ($M$ et $n$ seront demandés à l'utilisateur)
Méthode de l'espérance
On simule $n$ (grand) valeurs $x_i, 1\leq i\leq n$ suivant une loi uniforme sur $[0;1]$. Alors $\displaystyle\dfrac{\displaystyle\sum_1^n f(x_i)}{n}$ est une bonne approximation de $\displaystyle\int_0^1 f(x)dx$
Programmer et tester cette méthode ($n$ sera demandé à l'utilisateur)
Algorithmique : Méthodes de calcul approché d'une intégrale
Exercice
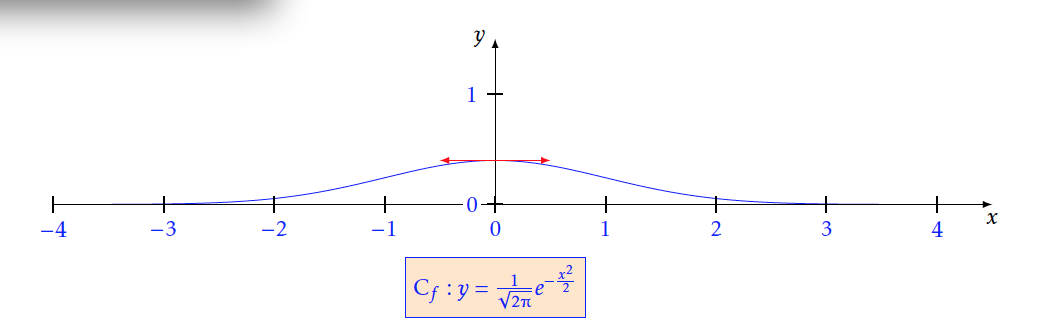
Soit $f$ la fonction définie sur $\mathbb{R}$par: $f(x) = \frac{1}{\sqrt {2\pi } }e^{ - \frac{{{x^2}}}{2}}$ On note $C_f$ le graphe représentatif de $f$ dans un rep ère $(O;I,J)$ du plan.
Partie A
- Démontrer que, pour tout $x$ de , $f(-x) = f(x)$. Que peut-on en déduire pour $C_f$ ?\\ $f(-x) = \frac{1}{{\sqrt {2\pi } }}{e^{ - \frac{{{(-x)^2}}}{2}}}= \frac{1}{{\sqrt {2\pi } }}{e^{ - \frac{{{x^2}}}{2}}}=f(x)$\\ On a pour tout $x \in \mathbb{R} ; f(-x)=f(x)$, ceci prouve que la fonction $f$ est paire , donc$C_f$ la représentation graphique de $f$ est symétrique par rapport à l'axe des ordonnées.
- Etudier le sens de variation de $f$ sur $\mathbb{R}{^ + }$.
$f$ est dérivable sur $\mathbb{R}$ et $f'(x)= \frac{1}{{\sqrt {2\pi } }}{(-x)e^{ - \frac{{{x^2}}}{2}}}=-xf(x)$
La fonction exponentielle étant strictement positive sur $\mathbb{R}$, $f'(x)$ a le signe de $-x$.
Donc pour tout $x>0$ on a $f'(x)<0$, ce qui prouve que la fonction $f$ est strictement décroissante sur $\mathbb{R} ^{+}$. - Construire $C_f$ dans le repère précédent. Figure
- Soit $ b$ un réel strictement positif. On cherche un encadrement de l'aire A du domaine compris entre $C_f$, l'axe $[0x)$ et les droites d'équation $x = 0$ et $x =b$.
- A l'aide d'un logiciel de géométrie dynamique, effectuer une conjecture sur cette aire pour $b = 3$.
- Avec $n=6$
- Avec $n=12$
- Avec $n=40$
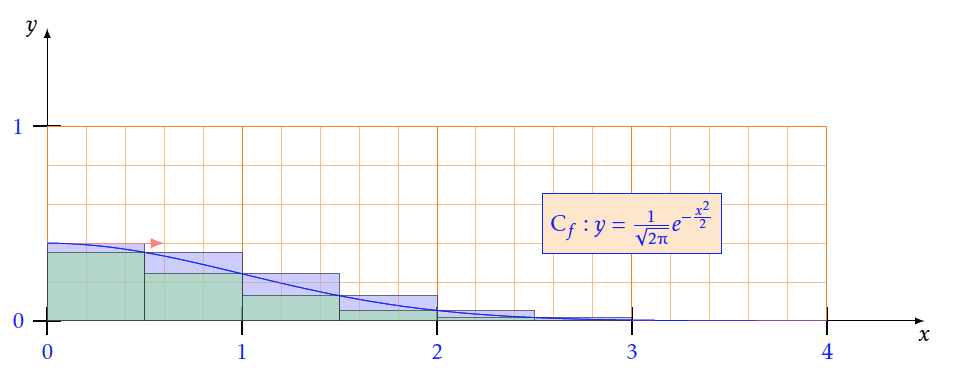
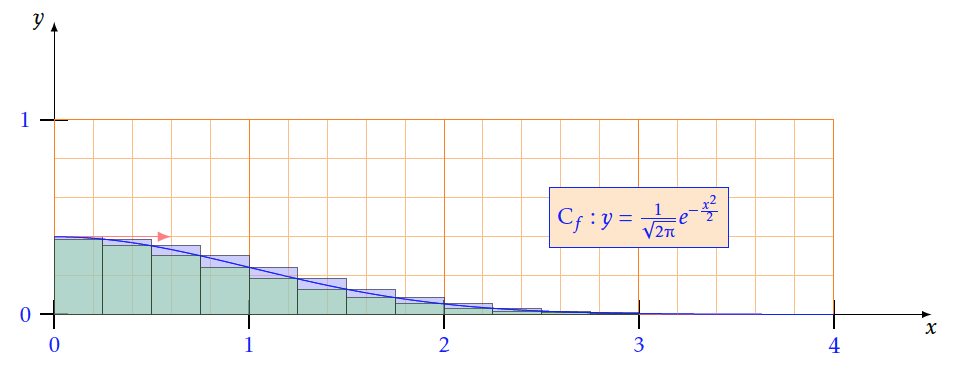
- Soit $f$ une fonction décroissante positive sur un intervalle $[a ; b]$ avec a$ < $b et n un entier$>$0. On définit $h=\frac{b-a}{n}$et on note I =$\displaystyle\int_a^bf\left(x\right)dx$ .Montrer que $h\sum\limits_{k = 1}^n {f(a + kh)} \le I \le h\sum\limits_{k = 0}^n {f(a + kh)} $
Posons $x_0=a$, $x_1=a+h$ et pour tout $k$ entier de $[0,n]$; $x_k=a+kh$ ;
on a $a=x_0< x_1 < \ldots< x_n=b$ $f$ est décroissante sur $[a,b]$, donc sur $[x_k;x_{k+1}]$;
Donc pour tout $x \in [x_k;x_{k+1}]$, on a $f\left (x_k\right )\geq f(x)\geq f\left (x_{k+1}\right )$
soit encore $f\left (x_{k+1}\right )\leq f(x)\leq f\left (x_{k}\right )$
On intègre sur l'intervalle $[x_k;x_{k+1}] $; on obtient $\displaystyle \int_{x_k}^{x_{k+1}} f\left (x_{k+1}\right )\,dx \leq \displaystyle \int_{x_k}^{x_{k+1}} f\left (x\right )\,dx\leq \displaystyle \int_{x_k}^{x_{k+1}} f\left (x_{k}\right )\,dx$
soit :$$h f\left (x_{k+1}\right ) \leq \displaystyle \int_{x_k}^{x_{k+1}} f\left (x\right )\,dx\leq h f\left (x_{k}\right )$$ Pour $k=0$ on a : $h f\left (x_{1}\right ) \leq \displaystyle \int_{x_0}^{x_{1}} f\left (x\right )\,dx\leq h f\left (x_{0}\right )$
Pour $k=1$ on a : $h f\left (x_{2}\right ) \leq \displaystyle \int_{x_1}^{x_{2}} f\left (x\right )\,dx\leq h f\left (x_{1}\right )$
Pour $k=2$ on a : $h f\left (x_{3}\right ) \leq \displaystyle \int_{x_2}^{x_{3}} f\left (x\right )\,dx\leq h f\left (x_{2}\right )$
$\cdots \cdots \cdots \cdots \cdots \cdots \cdots $
Pour $k=n-1$ on a : $h f\left (x_{n}\right ) \leq \displaystyle \int_{x_{n-1}}^{x_{n}} f\left (x\right )\,dx\leq h f\left (x_{n-1}\right )$
On ajoute membre à membres ces $n$ inégalités de même sens, et on utilise la relation de Chasles :
$$h\left [f\left (x_{1}\right )+f\left (x_{2}\right )+\cdots+f\left (x_{n}\right )\right ]\leq\displaystyle \int_{x_{0}}^{x_{n}} f\left (x\right )\,dx\leq h\left [f\left (x_{0}\right )+f\left (x_{1}\right )+\cdots+f\left (x_{n-1}\right )\right]$$ soit encore $h\sum\limits_{k = 1}^n {f(a + kh)} \le I \le h\sum\limits_{k = 0}^n {f(a + kh)} $ - En déduire un algorithme permettant d'encadrer I. $$\begin{array} {|l |l|}\hline \text{Valeur approchée d'une intégrale } & \\ & \\ \text{ Variables : } & n, k \text{ deux entiers naturels, }\\ & Som_{inf}, Som_{sup} \text{ deux réels, }\\ \text{Entrées :}& \text{ Saisir } a.\\ & \text{ Saisir } b.\\ & a \text{ et } b \text{ nombres réels, les bornes de l'intégrale} \\ & \text{ Saisir } n.\\ & n \text{ entier ,le nombre de rectangles utilisé pour faire l'approximation} \\ & \text{ Saisir } f.\\ & f \text{ fonction ,la fonction à intégrer sur [a;b]} \\ \text{Initialisation :}& \\ & Som_{inf} \text{ prend la valeur } 0.\\ & Som_{sup} \text{ prend la valeur } 0.\\ \text{ Traitement : } & \\ & h \text{ prend la valeur } \dfrac{b-a}{n}\\ & \text{ Pour } k \text{ variant de 1 à } n\\ & \quad \text{ Faire } \\ & \quad Som_{inf} \text{ prend la valeur } Som_{inf}+h\times f(a+kh).\\ & \quad Som_{sup} \text{ prend la valeur } Som_{sup}+h\times f(a+(k-1)h).\\& \text{ Fin Pour } \\ \text{ Sortie : } & \text{ Afficher } Som_{inf}\\ & \text{ Afficher } Som_{sup} \\ \hline \end{array}$$
- Transcrire cet algorithme en langage machine pour la fonction $f$ définie dans l'énoncé :
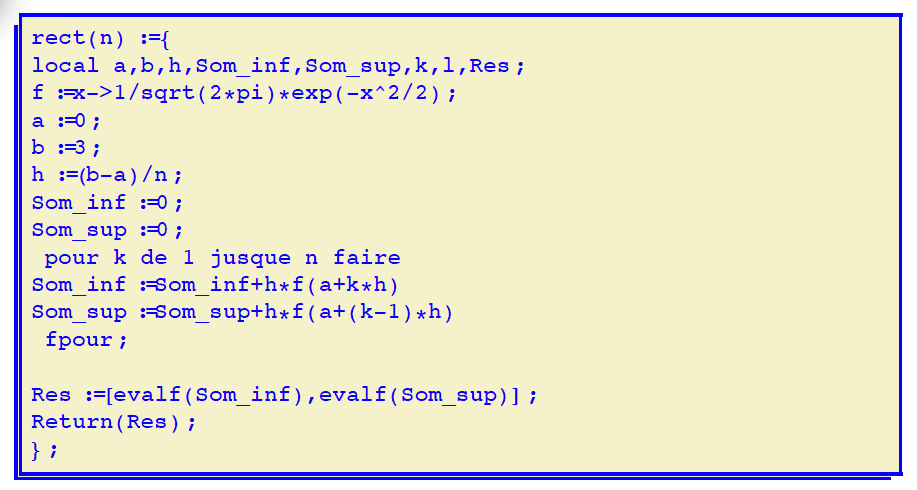
Son utilisation :rect(100);renvoie :[0.492731448412,0.504566761372]seq(rect(100*k),k=1..5);[0.492731448412,0.504566761372],[0.495691024443,0.501608680922],[0.496677439013,0.500622543333],[0.497170625526,0.500129453766],[0.497466530786,0.499833593378] - Quelle conjecture peut-on formuler sur l'aire du domaine compris entre $C_f$ et l'axe [Ox) ?
Cette aire vaut 1 unité d'aire ...( cf cours de probabilité)
Partie B
Dans la suite de l'exercice, on utilisera l'algorithme suivant, algorithme permettant de calculer la valeur approchée d'une intégrale sous la forme d'une fonction:
$$\begin{array} {|l |l|}\hline \text{Fonction Valeur approchée d'une intégrale } & \\ \text{Une approximation de l'intégrale par la méthode Simpson } & \\ & \\ \text{ Variables : } & n \text{ un entier naturel, }\\ & a, b \text{ deux réels, }\\ \text{Entrées :}& \\ & f \text{ fonction ,la fonction à intégrer sur [a;b]} \\ \text{Initialisation :}& \\ & S \text{ prend la valeur } 0.\\ & m \text{ prend la valeur } a.\\ \text{ Traitement : } & \\ & h \text{ prend la valeur } \dfrac{b-a}{n}\\ & \text{ Tant que } m < b\\ & \quad \text{ Faire } \\ & \quad S \text{ prend la valeur } S+S+(f(m)+4*f(m+h/2)+f(m+h))*(h/6).\\ & \quad m \text{ prend la valeur } m+h.\\ \text{ Sortie : } & \text{ Afficher } S.\\ \hline \end{array}$$
Avec XCAS : rect(n):={ local a,b,h,Som_inf,Som_sup,k,l,Res;
f:=x->1/sqrt(2*pi)*exp(-x^2/2);
a:=0; b:=3; h:=(b-a)/n;
Som_inf:=0; Som_sup:=0;
pour k de 1 jusque n
faire
Som_inf:=Som_inf+h*f(a+k*h)
Som_sup:=Som_sup+h*f(a+(k-1)*h)
fpour;
Res:=[evalf(Som_inf),evalf(Som_sup)]; Return(Res); };
Son utilisation : rect(100); renvoie : [0.492731448412,0.504566761372] seq(rect(100*k),k=1..5); renvoie :[0.492731448412,0.504566761372],[0.495691024443,0.501608680922],[0.496677439013,0.500622543333],[0.497170625526,0.500129453766],[0.497466530786,0.499833593378]
Exercice
- On considère la fonction $F$ définie sur $\mathbb{R}^+$ par : $F\left(t\right)=\displaystyle\int_0^t\dfrac{1}{\sqrt{2\pi{}}}e^{-\dfrac{x^2}{2}}dx$ Montrer que, pour tout réel $\alpha{}$ de ]0 ; 1], ,il existe un seul réel positif $b$ tel que $F\left(b\right)=0,5-\frac{\alpha{}}{2}$; $b$ est noté $u_{\alpha{}}$ .
- En utilisant l'algorithme donné précédemment, construire un algorithme permettant, pour un nombre $\alpha{}$donné de ]0 ; 1], de déterminer une valeur approchée de ${u_\alpha }$. $$\begin{array} {|l |l|}\hline \text{Approximation de } u_{\alpha} & \\ \text{Une approximation ... } & \\ & \\ \text{Entrées :}& \\ & \text{ Saisir } \alpha \text{ un réel de ]0;1] } \\ & \text{ Saisir } h \text{ le pas dans la méthode d'intégration } \\ & \text{ Saisir } f \text{ la fonction à intégrer sur [a;b] } \\ \text{Initialisation :}& \\ & b \text{ prend la valeur } 0.\\ & h \text{ prend la valeur } 0.01\\ \text{ Traitement : } & \\ & h \text{ prend la valeur } \dfrac{b-a}{n}\\ & \text{ Tant que } Simpson(0,b,0.01) < 0.5-alpha/2 \\ & \quad \text{ Faire } \\ & \quad S \text{ prend la valeur } S+S+(f(m)+4*f(m+h/2)+f(m+h))*(h/6).\\ & \quad b \text{ prend la valeur } b+h.\\ \text{ Sortie : } & \text{ Afficher } b.\\ \hline \end{array}$$
Déjà comme $\alpha \in ]0;1]$; on a $0,5-\frac{\alpha{}}{2} \in \left [0;\dfrac{1}{2}\right[$.
Il s'agit donc ici de déterminer un antécédent $b$ du nombre $0,5-\frac{\alpha{}}{2}$, on utilise ici le théorème de la bijection !
La fonction $f:x\mapsto \frac{1}{\sqrt{2\pi{}}}e^{-\frac{x^2}{2}}$ est continue sur $\mathbb{R}$, donc la fonction $F$ définie sur $\mathbb{R}^+$ par $F\left(t\right)=\int_0^t\frac{1}{\sqrt{2\pi{}}}e^{-\frac{x^2}{2}}dx$ est la primitive de $f$ qui s'annule en 0.
Ainsi $F$ est dérivable sur $\mathbb{R}^+$ et $F'(x)=f(x)$,
la fonction exponentielle étant strictement positive sur $\mathbb{R}$, on a donc :
$\forall x \in \mathbb{R}; F'(x)>0$
Par ailleurs $\lim\limits_{x\rightarrow +\infty}F(x)=\dfrac{1}{2}$
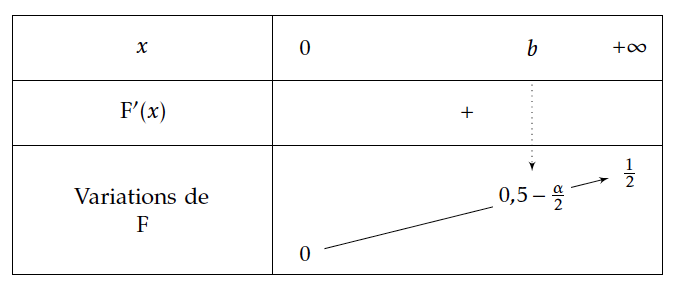
$F$ est donc continue car dérivable , strictement croissante sur $[0;+\infty[$,
donc $F$ réalise une bijection de $[0;+\infty[$ sur $\left[F(0);\lim\limits_{x\rightarrow +\infty}F(x)\right[$ soit sur $\left[0;\dfrac{1}{2}\right[$.
Or $0,5-\frac{\alpha{}}{2} \in \left [0;\dfrac{1}{2}\right[$,
donc l'équation $F(x)=0,5-\frac{\alpha{}}{2}$ a une solution unique $b$ dans $[0;+\infty[$.
- Vues: 23857
