Lois normales - Propriétés de la loi $\mathcal{N}(0;1)$
Propriétés de la loi $\mathcal{N}(0;1)$
Des propriétés faciles à mémoriser ...
|

|
|
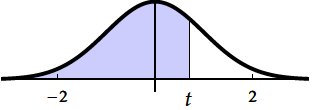
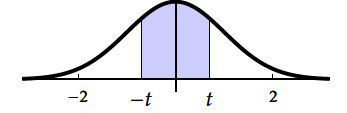
$$\begin{array}{|c|c|c| }P(X\leq t)=\Pi(t) & 1-P(X\leq t)=P(X\leq -t)=\Pi(-t) & P(-t\leq X\leq t) =\displaystyle\int_{-t}^t f(x)\;dx \\ & 1-\Pi(t)=\Pi(-t) & P(X\leq t)-P(X\leq -t)=\Pi(t)-\Pi(-t) \\ & & P(X\leq t)-P(X\leq -t)=\Pi(t)-\left [1-\Pi(t)\right ] \\ & & P(-t\leq X\leq t)=2\Pi(t)-1 \\ \end{array}$$
Espérance et variance
La fonction $x\mapsto e^{-\frac{x^2}{2}}$ ne peut pas se mettre sous la forme $u'e^{u}$ .
alors que $xe^{-\frac{x^2}{2}}=-\underbrace{\left (-x\right ) e^{-\frac{x^2}{2}}}_{\text{ Je reconnais } u'e^u }$
Donc $\displaystyle\int _a^b xe^{-\frac{x^2}{2}}\;dx =\left [-e^{-\frac{x^2}{2}}\right ]_a^b=-e^{-\frac{b^2}{2}}+e^{-\frac{a^2}{2}}$, avec $\displaystyle\lim_{a\to -\infty}e^{-\frac{a^2}{2}}=0$ et $\displaystyle\lim_{b\to +\infty}e^{-\frac{b^2}{2}}=0$
Donc $\displaystyle\lim_{a\to -\infty \\ b\to +\infty}\int _a^b xe^{-\frac{x^2}{2}}\;dx=0$ et ainsi $E(X)=0\times \dfrac{1}{\sqrt{2\pi}}=0$.
On admet $V(X)=1$ , donc $\sigma(X)=1$.
Un théorème
Déjà comme $\alpha \in ]0;1[$; on a $1-\alpha \in \left ]0;1\right[$.
Il s'agit donc ici de déterminer un antécédent $ u_{\alpha}$ du nombre $1-\alpha$, on utilise ici le théorème de la bijection !
La fonction $f:x\mapsto \frac{1}{\sqrt{2\pi{}}}e^{-\frac{x^2}{2}}$ est continue sur $\mathbb{R}$, donc la fonction $a$ définie sur $\mathbb{R}^+$ par $a\left(t\right)=\displaystyle\int_{-t}^t\frac{1}{\sqrt{2\pi{}}}e^{-\frac{x^2}{2}}dx$ est dérivable sur $\mathbb{R}^+$, en effet la fonction $F$ définie sur $\mathbb{R}^+$ par $F\left(t\right)=\displaystyle\int_{0}^t\frac{1}{\sqrt{2\pi{}}}e^{-\frac{x^2}{2}}dx$ est la primitive de $f$ sur $\mathbb{R}^+$ qui s'annule en 0.
Ainsi $F$ est dérivable sur $\mathbb{R}^+$ et $F'(x)=f(x)$,
On a ensuite $a\left(t\right)=\displaystyle\int_{-t}^t\frac{1}{\sqrt{2\pi{}}}e^{-\frac{x^2}{2}}dx=2\displaystyle\int_{0}^t\frac{1}{\sqrt{2\pi{}}}e^{-\frac{x^2}{2}}dx=2\;F(t)$
En dérivant, il vient : $a'(t)= 2\;F'(t)=2\;f(t)$ la fonction exponentielle étant strictement positive sur $\mathbb{R}$, on a donc :
$\forall t \in \mathbb{R}^+; a'(t)>0$
Par ailleurs $\lim\limits_{t\rightarrow +\infty}F(t)=\dfrac{1}{2}$, donc $\lim\limits_{t\rightarrow +\infty}a(t)=1$
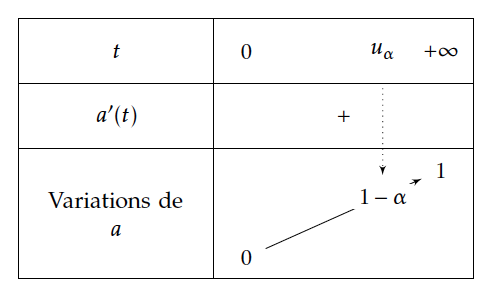
$a$ est donc continue car dérivable , strictement croissante sur $[0;+\infty[$,
donc $a$ réalise une bijection de $[0;+\infty[$ sur $\left[a(0);\lim\limits_{t\rightarrow +\infty}a(t)\right[$ soit sur $\left[0;1\right[$.
Or $1-\alpha \in \left [0;1\right[$,\enc{ donc l'équation $a(t)=1-\alpha$ a une solution unique $u_{\alpha}$ dans $[0;+\infty[$.}
- Pour $\alpha =0,05$ : $2\Pi(t)-1=0,05$ équivaut à $\Pi(t)=\dfrac{1,95}{2}=0,975\approx \Pi(1,96)$ \enc{$u_{0,05}\approx 1,96$}
- Pour $\alpha =0,01$ : $2\Pi(t)-1=0,01$ équivaut à $\Pi(t)=\dfrac{1,99}{2}=0,995\approx \Pi(2,58)$ \enc{$u_{0,01}\approx 2,58$}
Les lois $\mathcal{N}(\mu;\sigma^2)$ d'espérance $\mu >0$ et d'écart-type $\sigma>0$
Définition
La loi $\mathcal{N}(\mu;\sigma^2)$ possède une densité $f_{\mu,\sigma}$ définie sur $\mathbb{R}$ par $f_{\mu,\sigma}(x)=\frac{1}{\sigma\sqrt { 2\Pi }}e^{ - \frac{ 1 }{2}\left (\dfrac{x-\mu}{\sigma} \right )^2}$
Sur la calculatrice $Y_1=normalFdp(X,\mu,\sigma)$ On a $P(a\leq X_{\mu,\sigma}\leq b)\approx normalFr\text{é}p(a,b,\mu,\sigma)$
Un résultat à savoir
- $P(\mu-\sigma\leq X_{\mu,\sigma}\leq \mu+\sigma)\approx 0,683$
- $P(\mu-2\sigma\leq X_{\mu,\sigma}\leq \mu+2\sigma)\approx 0,954$
- $P(\mu-3\sigma\leq X_{\mu,\sigma}\leq \mu+3\sigma)\approx 0,997$
$X_{\mu,\sigma} \in\left [\mu-3\sigma;[\mu-3\sigma\right ] $ équivaut à $-3\leq \dfrac{X-\mu}{\sigma}\leq 3$ ( car $\sigma>0$)
- $P\left (X_{\mu,\sigma} \in\left [\mu-3\sigma; \mu+3\sigma\right ]\right ) =P\left (-3\leq \dfrac{X-\mu}{\sigma}\leq 3\right )=2\Pi(3)-1\approx 2\times0,998\,65-1=0,9973$.
- $P\left (X_{\mu,\sigma} \in\left [\mu-2\sigma; \mu+2\sigma\right ]\right ) =P\left (-2\leq \dfrac{X-\mu}{\sigma}\leq 2\right )=2\Pi(2)-1\approx 2\times0,9772-1=0,9544$.
- $P\left (X_{\mu,\sigma} \in\left [\mu-\sigma; \mu+\sigma\right ]\right ) =P\left (-1\leq \dfrac{X-\mu}{\sigma}\leq 1\right )=2\Pi(1)-1\approx 2\times0,8413-1=0,6826$.
$P\left (X_{\mu,\sigma} \in\left [\mu-3\sigma; \mu+3\sigma\right ]\right )\approx 0,99 $
$P\left (X_{\mu,\sigma} \in\left [\mu-2\sigma; \mu+2\sigma\right ]\right )\approx 0,95$
$P\left (X_{\mu,\sigma} \in\left [\mu-\sigma; \mu+\sigma\right ]\right )\approx 0,68 $
Retour sur l'exemple introductif
Soit $Y$ la variable aléatoire qui compte le nombre de boules vertes tirées lors des 870 tirages avec remise: $Y$ suit la loi $\mathcal{B}(870;0,791)$ d'espérance mathématique $870\times 0,791\approx 688$ et d'écart-type $\sqrt{870\times 0,791\times 0,209}\approx 12$.
$P(Y\leq 339)=P\left (\dfrac{Y- 688}{12}\leq \dfrac{339-688}{12}\right )\approx P\left (\dfrac{Y- 688}{12}\leq-29\right ).$
On approche $\dfrac{Y- 688}{12}$ par la loi $\mathcal{N}(0;1)$ donc $P(Y\leq 339)\approx \Pi(-29)\approx 0$.
On est contraint de remettre en cause le choix des jurés.
$P(X_{688,12}\leq 339)\approx P\left (\dfrac{X_{688,12}- 688}{12}\leq -29\right )=\Pi(-29).$
Tout se passe comme si on approchait $Y$ par $X_{688,12}$.
- Vues: 22989
