Baccalauréat STI2D NOUVELLE CALÉDONIE 2013 - Exercice 3

Page 5 sur 8: Exercice 3

Exercice 3 7 points

Fonctions logarithmes

Partie A

---

$f$ est une fonction définie et dérivable sur l'intervalle $]0 ; +\infty[$. $f'$ désigne la fonction dérivée de $f$.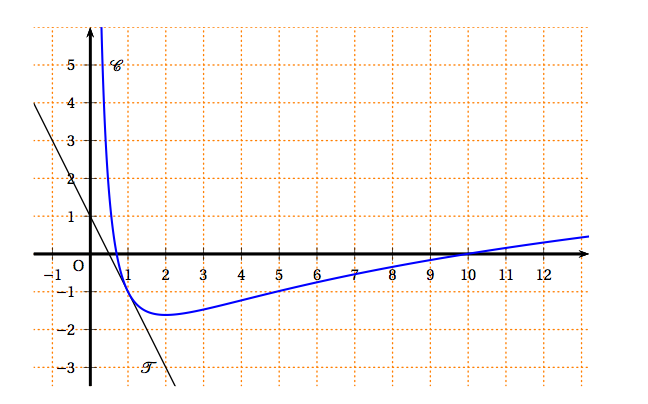

• $\mathcal{C}$ est la représentation graphique de la fonction $f$ dans un repère orthonormal.
• $T$ est la tangente à $\mathcal{C}$ au point de coordonnées $(1 ; -1)$. $T$ passe par le point de coordonnées $(0;1)$.

---

1. 1. Par lecture graphique, déterminer $f(1)$.
   2. Déterminer $f'(1)$.
   3. Donner une équation de $T$.
2. On sait que $f(x)$ est de la forme $f(x) = 2\ln x+ \dfrac{a}{x} + b$ où $a$ et $b$ sont des nombres réels.
   1. Calculer $f'(x)$.
   2. Déterminer alors les valeurs de $a$ et $b$.

---

Partie B

---

Soit la fonction $f$ définie et dérivable sur $]0 ; +\infty[$ par $f(x) = 2\ln x + \dfrac{4}{x} - 5$.

1. 1. Déterminer $\displaystyle\lim_{x \to + \infty} f(x)$.
   2. On admet que $\displaystyle\lim_{x \to 0} f(x) = + \infty$. Que peut-on en déduire graphiquement ?
2. 1. Pour tout nombre réel $x$ appartenant à $]0 ; +\infty[$, vérifier que $f'(x) = \dfrac{2x - 4}{x^2}$.
   2. Étudier le signe de $f'(x)$ sur $]0 ; +\infty[$.
3. Établir le tableau de variations de $f$ sur $]0 ; +\infty[$.
4. En précisant votre démarche, donner le nombre de solution(s) de l'équation $f(x) = 0$, pour $x$ appartenant à $]0 ; +\infty[$.
5. 1. Donner le signe de $f(x)$ pour $x$ appartenant à $[1 ; 3]$.
   2. On admet que la fonction $F$ définie pour $x$ appartenant à $]0 ; +\infty[$ par $F(x) = (2x + 4) \ln x - 7x$ est une primitive de $f$. Déterminer l'aire $\mathcal{A}$ du domaine limité par la courbe $\mathcal{C}$, l'axe des abscisses et les droites d'équation $x = 1$ et $x = 3$ en unités d'aires. On donnera la valeur exacte puis une valeur approchée à $10^{-2}$ près de $\mathcal{A}$.