Baccalauréat STI2D NOUVELLE CALÉDONIE 2013 - Correction Exercice 3
Page 6 sur 8
Correction de l'exercice 3 (7 points)
Partie A
$f$ est une fonction définie et dérivable sur l'intervalle $]0 ; +\infty[$. $f'$ désigne la fonction dérivée de $f$. 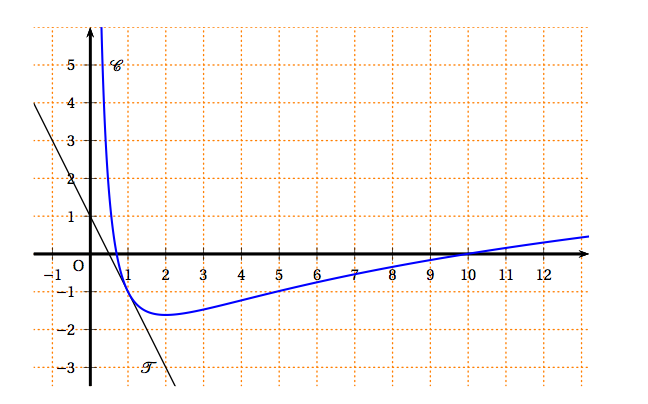
- $\mathcal{C}$ est la représentation graphique de la fonction $f$ dans un repère orthonormal.
- $T$ est la tangente à $\mathcal{C}$ au point de coordonnées $(1 ; -1)$. $T$ passe par le point de coordonnées $(0;1)$.
-
- Par lecture graphique, déterminer $f(1)$. On lit $f(1) \approx - 1$.
- Déterminer $f'(1)$. $f'(1)$ est le coefficient directeur de la tagente $T$ à $\mathcal{C}$ au point de coordonnées $(1 ; -1)$.
- Donner une équation de $T$.
- Méthode 1 : Son coefficient directeur est égal à $- 2$ et son ordonnée à l'origine 1 ; l'équation de $\mathcal{T}$ est donc $y = - 2x + 1$.
- Méthode 2 :
La tangente $\1$ à $\2$ au point d'abscisse $a= \3$ a pour équation : $$y=\6'(\3)(x-\3)+\6(\3)$$ Ici $a= \3$, on calcule successivement :
- $\6\left(\3 \right)=\4$
- $\6'\left (\3\right )=\5$
Ainsi $\1:y=\5\left (x-\3\right )+\4$
l'équation de $\mathcal{T}$ est donc $y = - 2x + 1$.
$f(1)=- 1$.
On lit $f'(1) = \dfrac{y_B-y_A}{x_B-x_A}=\dfrac{-2}{1} = - 2$.$f'(1)=- 2$. - On sait que $f(x)$ est de la forme $f(x) = 2\ln x+ \dfrac{a}{x} + b$ où $a$ et $b$ sont des nombres réels.
- Calculer $f'(x)$. $f'(x) = 2\times\dfrac{1}{x} - \dfrac{a}{x^2} = \dfrac{2x - a}{x^2}$.
- Déterminer alors les valeurs de $a$ et $b$. On sait que $f'(1) = - 2$ soit $\dfrac{2\times 1 - a}{1^2} = - 2 \iff 2 - a = - 2 \iff a = 4$.
Donc $f(x) = 2\ln x + \dfrac{4}{x} + b$. mais on sait que $f(1) = - 1$, soit $2\ln 1 + \dfrac{4}{1} + b = - 1 \iff b = - 1 - 4 = - 5$.Finalement : $f(x) = 2\ln x + \dfrac{4}{x} - 5$.
Partie B
Soit la fonction $f$ définie et dérivable sur $]0 ; +\infty[$ par $f(x) = 2\ln x + \dfrac{4}{x} - 5$.
-
- Déterminer $\displaystyle\lim_{x \to + \infty} f(x)$. On sait que $\displaystyle\lim_{x \to + \infty} \ln x = + \infty$ et que $\displaystyle\lim_{x \to + \infty} \dfrac{4}{x}$, d'où par somme de limites $\displaystyle\lim_{x \to + \infty} f(x) = + \infty$.
- On admet que $\displaystyle\lim_{x \to 0} f(x) = + \infty$. Que peut-on en déduire graphiquement ? $\displaystyle\lim_{x \to 0} f(x) = + \infty$ signifie que l'axe des ordonnées est asymptote verticale à $\mathcal{C}$ au voisinage de zéro.
-
- Pour tout nombre réel $x$ appartenant à $]0 ; +\infty[$, vérifier que $f'(x) = \dfrac{2x - 4}{x^2}$. On a $f'(x) = 2 \times \dfrac{1}{x} - \dfrac{4}{x^2} = \dfrac{2x - 4}{x^2}$.
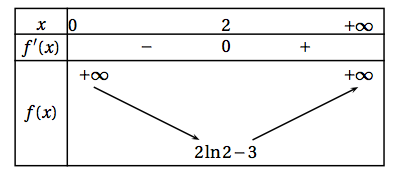
- Étudier le signe de $f'(x)$ sur $]0 ; +\infty[$.
- Établir le tableau de variations de $f$ sur $]0 ; +\infty[$. Comme $x^2 > 0$ si $x \in ]0~;~ +\infty[$, le signe de $f'(x)$ est celui de $2x - 4$ qui est positif si $x > 2$.
- $f'(x) > 0$ sur $]2~;~+ \infty[$ ;
- $f'(x) < 0 sur ]0~;~2[$ ;
- $f'(2) = 0$.
- En précisant votre démarche, donner le nombre de solution(s) de l'équation $f(x) = 0$, pour $x$ appartenant à $]0 ; +\infty[$. Comme $2\ln 2 - 3 \approx - 1,62$ est inférieur à zéro, la fonction décroissant de plus l'infini à $2\ln 2 - 3$ s'annule une fois sur l'intervalle ]0~;~2[, puis croissant de $2\ln 2 - 3$ à plus l'infini s'annule une autre fois sur l'intervalle $]2~;~+ \infty[$. L'équation $f(x) = 0$, pour $x$ appartenant à $]0~;~ +\infty[$ a donc deux solutions $\alpha$ et $\beta$.
-
- Donner le signe de $f(x)$ pour $x$ appartenant à $[1 ; 3]$. On a $f(1) = 2 \times 0 \dfrac{4}{1} - 5 = - 1$ et $f(3) = 2 \ln 3 + \dfrac{4}{3} - 5 = 2\ln 3 - \dfrac{11}{3} \approx - 1,47$.
- On admet que la fonction $F$ définie pour $x$ appartenant à $]0 ; +\infty[$ par $F(x) = (2x + 4) \ln x - 7x$ est une primitive de $f$. Déterminer l'aire $\mathcal{A}$ du domaine limité par la courbe $\mathcal{C}$, l'axe des abscisses et les droites d'équation $x = 1$ et $x = 3$ en unités d'aires. On donnera la valeur exacte puis une valeur approchée à $10^{-2}$ près de $\mathcal{A}$. On a vu que sur l'intervalle [1~;~3], $f$ est négative, donc l'aire $\mathcal{A}$ du domaine limité par la courbe $\mathcal{C}$, l'axe des abscisses et les droites d'équation $x = 1$ et $x = 3$ est égale à $$\begin{array}{ll}\mathcal{A} = & \displaystyle\int_{1}^3 -f(x)\:\text{d}x \\ &= - \left[F(3) - F(1) \right] \\ &= F(1) - F(3) \\ &= (2\times 1 + 4) \ln 1 - 7\times 1 - \left[(2\times 3 + 4) \ln 3 - 7\times 3 \right] \\ &= - 7 - 10\ln 3 + 21 \\ &= 14 - 10\ln 3 ~\text{(unités d'aire).} \end{array}$$
Donc sur l'intervalle $[1~;~3]$, $f$ ne prend que des valeurs négatives.On a $\mathcal{A} = 14 - 10\ln 3 \approx 3,01$~unités d'aire.
Conclusion :
Exercice 4
- Vues: 17377
