Bac STI2D Antilles Guyane 22 juin 2015 - Correction Exercice 2
Correction de l'exercice 2 (5 points)
Exercice 2 5 points
Les trois parties de cet exercice peuvent être traitées de manière indépendante.
Dans cet exercice, ln désigne la fonction logarithme népérien.
Partie A
On considère la fonction $f$ définie sur $]0~;~+ \infty[$ par : \[f(x) = ax + b\ln (x) + 1\] où $a$ et $b$ sont deux nombres réels. $C_f$ est la représentation graphique de la fonction $f$ dans un repère orthonormé. Les points A et E sont deux points de la courbe $C_f$. Le point A a pour coordonnées $(1~;~2)$ et le point E a pour abscisse 4. La tangente à $C_f$ au point E est horizontale. 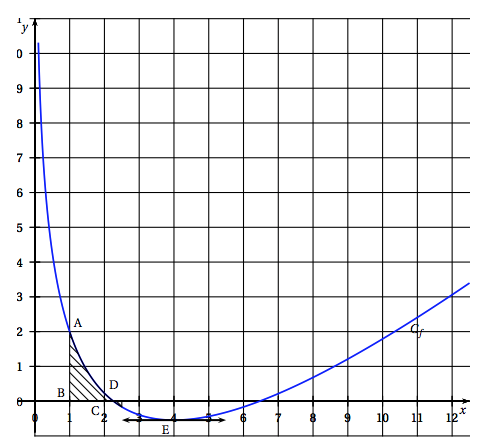
- Déterminer $f(1)$ et $f'(4)$ où $f'$ désigne la fonction dérivée de $f$. Comme $A(1; 2)\in C_f$; on déduit que $f(1)= 2$
- Calculer $f'(x)$ puis exprimer $f'(4)$ en fonction de $a$ et $b$. Ayant $f(x) = ax + b\ln (x) + 1$, on déduit : $$f'(x)= a+b\times \dfrac{1}{x}$$ En effet $\left(\ln x\right)'= \dfrac{1}{x}$
- Déterminer les valeurs de $a$ et $b$. $$f(2)=1\iff a+b\ln 1 + 1 =2 \iff a+1 = 2\iff a = 1$$ $$f'(4) = 0\iff a +\dfrac{b}{4}= 0 \iff \dfrac{b}{4}= -1\iff b =-4$$
La tangente à $C_f$ au point d'abscisse 4 est horizontale, donc $f'(4)=0$.
$$f'(4)= a+\dfrac{b}{4}$$
$a = 1$ et $b =-4$
Partie B
Soit la fonction $f$ définie sur $]0~;~+ \infty[$ par: \[f(x) = x - 4\ln (x) + 1\]
- Déterminer $\displaystyle\lim_{x \to 0} f(x)$ en justifiant la réponse. Donner une interprétation graphique du résultat. $\left.\begin{array}{l} \lim\limits_{x \to 0}~x+1=1\\ \lim\limits_{x \to 0}~-\ln x=+\infty \end{array}\right\}$ par somme on obtient: $\lim\limits_{x \to 0}f(x)=+\infty$ Comme $\lim\limits_{x \to 0}f(x)=+\infty$ on déduit que la droite d'équation $x=0$ est asymptote verticale à $C_f$
- Déterminer $\displaystyle\lim_{x \to + \infty} f(x)$ en justifiant la réponse (on pourra factoriser l'expression de $f(x)$ par $x$). On écrit $f(x) = x\left(1+ \dfrac{1}{x}- \dfrac{\ln x}{x}\right)$ On utilise la limite de référence : $\displaystyle\lim_{x \to + \infty}\dfrac{\ln x}{x}= 0$
- Calculer la dérivée $f'$ de $f$. En déduire le tableau des variations de $f$. $$\begin{array}{rl}f'(x)&= 1-\dfrac{4}{x}\\ &=\dfrac{x}{x}-\dfrac{4}{x}\\ &=\dfrac{x-4}{x} \end{array}$$ On étudie alors le signe de la dérivée sur $]0~;~+ \infty[$
- Calculer la dérivée $G'$ de $G$. $$G(x) = x\ln (x) - x=x\left( \ln x -1\right)$$ $G=uv$ , donc $G'=u'v+v'u$ $$\begin{array}{rl}G'(x)&= 1\left( \ln x -1\right) +x\times \dfrac{4}{x} \\ &= \ln x -1 +1 \\ &=\ln x \end{array}$$
- En déduire une primitive $F$ de la fonction $f$ donnée dans la partie B sur $]0~;~+ \infty[$. On a $$\begin{array}{rl}f(x)&= x - 4\ln (x) + 1\\ &= x+1- 4\ln x \\ &=x+1-4G'(x) \end{array}$$ Une primitive de $f$ est donc la fonction $F$ définie sur $]0~;~+ \infty[$ par : $$\begin{array}{rl} F(x)&= \dfrac{x^2}{2}+x-4G(x)\\ &= \dfrac{x^2}{2}+x-4\left(x\ln (x) - x\right)\\ &= \dfrac{x^2}{2}+5x-4x\ln (x) \end{array}$$
- Déterminer la valeur exacte de l'aire de la pièce en unité d'aire ; puis en donner une valeur arrondie à $10^{-2}$. D'après le grahique $C_f$ est située au desssus de l'axe des abscisses sur $[1; 2]$ , ainsi $f$ est continue et positive sur $[1; 2]$. L' aire de la piéce exprimée en unités d'aires vaut donc : $$\begin{array}{rl} A&= \int_1^2 f(x) dx\\ &= F(2)-F(1)\\ F(2)&= \dfrac{2^2}{2}+5\times 2-4\times 2\ln 2\\ &= 12-8\ln 2\\ F(1)&= \dfrac{1^2}{2}+5\times 1-4 \ln 1\\ &= \dfrac{11}{2}\\ &\\ A&= 12-8\ln 2- \dfrac{11}{2}\\ A&= \dfrac{13}{2}-8\ln 2 \\ \end{array}$$
$\left.\begin{array}{l} \lim\limits_{x \to +\infty}~1+ \dfrac{1}{x}=1\\ \lim\limits_{x \to +\infty}~- \dfrac{\ln x}{x}=0 \end{array}\right\}$ par somme on obtient: $\lim\limits_{x \to+\infty}1+ \dfrac{1}{x}- \dfrac{\ln x}{x}=1$
$\left.\begin{array}{l} \lim\limits_{x \to +\infty}~x=+\infty\\ \lim\limits_{x \to +\infty}~1+ \dfrac{1}{x}- \dfrac{\ln x}{x}=1 \end{array}\right\}$ par produit on obtient: $\lim\limits_{x \to+\infty}f(x)=+\infty$
$\lim\limits_{x \to+\infty}f(x)=+\infty$
On peut par exemple faire un tableau de signes:
$$\begin{array}{|l|cccccr|} \hline x &0& & & 4 & & &+\infty\\
\hline \text{ Signe de } x& 0& & + & & + && \\ \hline \text{ Signe de } x-4 && & - & 0 & + &&\\ \hline \text{ Signe de } f'(x) & \| && - & 0 &+ & & \\ \hline \end{array}$$
On peut aussi plus simplement remarquer que sur $]0~;~+ \infty[$, on a $x> 0$, et donc $f'(x)$ a le signe de $x-4$, on dresse alors le tableau de variations de $f$ : 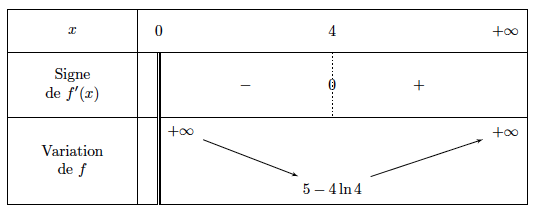
Partie C
Une entreprise fabrique des pièces de carrosserie de voiture.
La forme d'une pièce est donnée sur la figure ci-contre et correspond à la zone hachurée sur le graphique de la page précédente. On souhaite déterminer la mesure de l'aire de la pièce en unité d'aire. Le point D est le point de la courbe $C_f$ d'abscisse 2. Les points B et C ont pour coordonnées respectives $(1~;~0)$ et $(2~;~0)$. 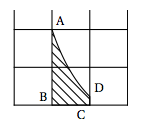
Soit la fonction $G$ définie sur $]0~;~+ \infty[$ par : \[G(x) = x\ln (x) - x.\]
- Vues: 25122
