Baccalauréat S Centres étrangers 12 juin 2013 - Correction de l'Exercice 3
Exercice 3 5 points
On considère la fonction $g$ définie pour tout réel $x$ de l'intervalle $[0 ; 1]$ par :
\[g(x) = 1 + \mathrm{e}^{-x}.\]
On admet que, pour tout réel $x$ de l'intervalle $[0 ; 1]$, $g(x) >0$.
On note $\mathscr{C}$ la courbe représentative de la fonction $g$ dans un repère orthogonal, et $\mathscr{D}$ le domaine plan compris d'une part entre l'axe des abscisses et la courbe $\mathscr{C}$, d'autre part entre les droites d'équation $x = 0$ et $x = 1 $.
La courbe $\mathscr{C}$ et le domaine $\mathscr{D}$ sont représentés ci-dessous.
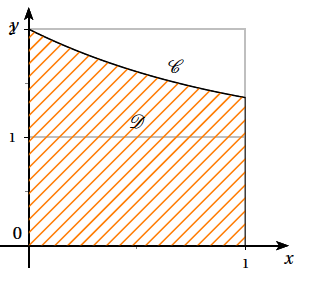
Le but de cet exercice est de partager le domaine $\mathscr{D}$ en deux domaines de même aire, d'abord par une droite parallèle à l'axe des ordonnées (partie A), puis par une droite parallèle à l'axe des abscisses (partie B).
Partie A
Soit $a$ un réel tel que $0\leqslant a\leqslant 1$. On note $\mathscr{A}_{1}$ l'aire du domaine compris entre la courbe $\mathscr{C}$, l'axe $(Ox)$,les droites d'équation $x = 0$ et $x =a$ , puis $\mathscr{A}_{2}$ celle du domaine compris entre la courbe $\mathscr{C}$, $(Ox)$ et les droites d'équation $x = a$ et $x = 1$. $\mathscr{A}_{1}$ et $\mathscr{A}_{2}$ sont exprimées en unités d'aire.
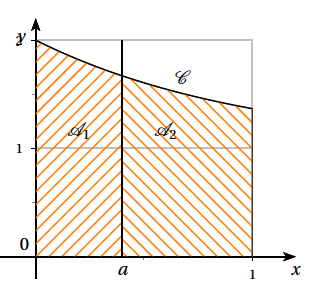
-
- Démontrer que $\mathscr{A}_{1}= a - \mathrm{e}^{-a} + 1$. $\mathscr{A}_1 = \displaystyle \int_0^a g(x)\text{d}x = \left[ x-\text{e}^{-x}\right]_0^a = a - \text{e}^{-a} + 1$
- Exprimer $\mathscr{A}_{2}$ en fonction de $a$. $\mathscr{A}_2 = \displaystyle \int_a^1 g(x)\text{d}x = \left[ x-\text{e}^{-x}\right]_a^1 = 1 - \text{e}^{-1} – a + \text{e}^{-a}$
$~$
$~$ - Soit $f$ la fonction définie pour tout réel $x$ de l'intervalle $[0 ; 1]$ par :
\[f(x) =2x - 2\,\mathrm{e}^{- x} + \dfrac{1}{\mathrm{e}}.\]
- Dresser le tableau de variation de la fonction $f$ sur l'intervalle $[0 ; 1]$. On précisera les valeurs exactes de $f(0)$ et $f(1)$. La fonction $f$ est une somme de fonctions dérivables sur $[0;1]$. Elle l’est donc aussi.
- Démontrer que la fonction $f$ s'annule une fois et une seule sur l'intervalle $[0 ; 1]$. en un réel $\alpha$. Donner la valeur de $\alpha$ arrondie au centième.
- $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = \left[\2 ; \3\right]$.
- $\1$ est strictement décroissante sur l' intervalle $I = \left[\2 ; \3\right]$.
- $\1\left(\2\right)=\4$ et $\1\left(\3\right)=\5$
$f’(x) = 2 + 2\text{e}^{-x} > 0$ puisque la fonction exponentielle est toujours positive.
D'après le théorème de la bijection :$0,452 < \alpha < 0,453$ donc $\alpha \approx 0,45$
$\6$ est compris entre $\5$ et $\4$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left[\2 ; \3\right]$ . - En utilisant les questions précédentes, déterminer une valeur approchée du réel $a$ pour lequel les aires $\mathscr{A}_{1}$ et $\mathscr{A}_{2}$ sont égales. $$\begin{array}{l} \text{Les} 2 \text{ aires sont égales} &\Leftrightarrow a - \text{e}^{-a} + 1 = 1 - \text{e}^{-1} – a + \text{e}^{-a} \\ & \Leftrightarrow 2a – 2\text{e}^{-a} + \text{e}^{-1} = 0 \\ & \Leftrightarrow f(a) = 0 \end{array} $$
Une valeur approchée de la solution est donc $0,45$.
$~$
Partie B
Soit $b$ un réel positif.
Dans cette partie, on se propose de partager le domaine $\mathscr{D}$ en deux domaines de même aire par la droite d'équation $y=b$. On admet qu'il existe un unique réel $b$ positif solution.
- Justifier l'inégalité $b<1 + \dfrac{1}{\mathrm{e}}$. On pourra utiliser un argument graphique. Il faut que $b < g(1)$ car sinon la portion de $\mathscr{D}$ au-dessus de la droite est inférieure à $(2-g(1)) \times (1-0) = 2-(1+\text{e}^{-1} )= 1 - \text{e}^{-1}$ (aire du rectangle incluant cette portion).
- Déterminer la valeur exacte du réel $b$. On veut que $\displaystyle \int_0^1 g(x)\text{d}x – b\times(1-0) = b \times (1-0) \Leftrightarrow \int_0^1 g(x) \text{d}x = 2b$
L’aire de la portion de $\mathscr{D}$ sous la droite est donc supérieure à $g(1) \times (1-0) = 1 + \text{e}^{-1}$.
Par conséquent :
$$ \begin{array}{l} b &= \dfrac{1}{2} \int_0^1 g(x)\text{d}x \\ & = \dfrac{1}{2} \left[ x - \text{e}^{-x} \right]_0^1 \\ &=\dfrac{1}{2}((1 - \text{e}^{-1} + 1) \\ &=\dfrac{1}{2}(2-\text{e}^{-1}) \end{array} $$
- Vues: 22757
