Baccalauréat S Polynésie 14 juin 2017 - Correction Exercice 1
Correction de l'exercice 1 (6 points)
La société Fibration fournit des abonnements Internet et des abonnements de téléphone mobile. Un client de la société Fibration souscrit soit un abonnement Internet, soit un abonnement de téléphone mobile, il ne cumule pas les deux. En cas de difficulté, la société Fibration propose à ses clients une ligne d'assistance téléphonique : le client doit d'abord signaler s'il est client Internet ou s'il est client mobile puis son appel est mis en attente de réponse par un opérateur.
Les parties A, B et C sont indépendantes.Si nécessaire, les résultats seront arrondis à $10^{-3}$.
Partie A - Durée d'attente
- Dans cette question, on s'intéresse à la durée d'attente d'un client Internet lorsqu'il contacte l'assistance téléphonique avant de joindre un opérateur. Une étude permet de modéliser cette durée d'attente en minutes par la variable aléatoire $D_1$ qui suit la loi exponentielle de paramètre $0,6$.
- Quelle est la durée d'attente moyenne que peut espérer un client Internet qui appelle cette ligne d'assistance ? La variable aléatoire $D_1$ suit la loi exponentielle de paramètre $0,6$.
- Calculer la probabilité que la durée d'attente d'un client Internet choisi au hasard soit inférieure à $5$ minutes. On veut calculer :
Par conséquent $E\left(D_1\right)=\dfrac{1}{0,6}\approx 1,667$
Le temps d’attente moyen est d’environ $1,667$ minutes soit environ $1$minute $40,02$ secondes.
$\quad$
$$\begin{array}{rl} P\left(D_1\leqslant 5\right)&=1-\text{e}^{-0,6\times 5} \\
&=1-\text{e}^{-3}\\
&\approx 0,950
\end{array}$$
La probabilité que la durée d’attente d’un client Internet choisi au hasard soit inférieure à $5$ minutes est environ $0,950$.
$\quad$ - Dans cette question, on s'intéresse à la durée d'attente d'un client mobile lorsqu'il contacte l'assistance téléphonique avant de joindre un opérateur. On modélise cette durée d'attente en minutes par la variable aléatoire $D_2$ qui suit une loi exponentielle de paramètre $\lambda$,\: $\lambda$ étant un réel strictement positif.
- Sachant que $P\left(D_2 \leqslant 4\right) = 0,798$, déterminer la valeur de $\lambda$. La variable aléatoire $D_2$ suit une loi exponentielle de paramètre $\lambda$.
- En prenant $\lambda = 0,4$, peut-on considérer que moins de 10 % des clients mobile choisis au hasard attendent plus de 5 minutes avant de joindre un opérateur ? $P\left(D_2\geqslant 5\right)=\text{e}^{-0,4\times 5} \approx 0,135 > 0,1$.
$\begin{align*} P\left(D_2\leqslant 4\right)=0,798 &\iff 1-\text{e}^{-4\lambda}=0,798 \\
&\iff -\text{e}^{-4\lambda}=0,798-1\\
&\iff \text{e}^{-4\lambda}=0,202 \\
&\iff -4\lambda = \ln (0,202) \\
&\iff \lambda =\dfrac{\ln(0,202)}{-4}
\end{align*}$
$\quad$
On peut donc pas considérer que moins de $10\%$ des clients mobile choisis au hasard attendent plus de $5$ minutes avant de joindre un opérateur.
$\quad$
Partie B - Obtention d'un opérateur
Si la durée d'attente avant l'obtention d'un opérateur dépasse 5 minutes, l'appel prend automatiquement fin. Sinon, l'appelant obtient un opérateur. On çhoisit au hasard un client qui appelle la ligne d'assistance. On admet que la probabilité que l'appel émane d'un client Internet est $0,7$. De plus, d'après la partie A, on prend les données suivantes : Si l'appel provient d'un client Internet alors la probabilité d'obtenir un opérateur est égale à $0,95$. Si l'appel provient d'un client mobile alors la probabilité d'obtenir un opérateur est égale à $0,87$.
- Déterminer la probabilité que le client joigne un opérateur. On appelle :
- Un client se plaint que son appel a pris fin après $5$ minutes d'attente sans avoir obtenu d'opérateur. Est-il plus probable que ce soit un client Internet ou un client mobile ? On a : $p\left(\overline{A}\right)=1-0,926=0,074$
– $I$ l’événement “L’appel provient d’un client Internet”;
– $M$ l’événement “l’appel provient d’un client mobile”;
– $A$ le client a joint un opérateur de l’assistance téléphonique.
On obtient ainsi l’arbre pondéré suivant :
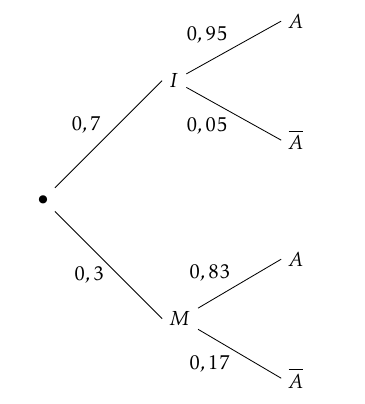
D’après la formule des probabilités totale, on a :
$\begin{align*} p(A)&=p(I\cap A)+p(M\cap A) \\
&=0,7\times 0,95+0,3\times 0,87 \\
&=0,926
\end{align*}$
La probabilité que le client joigne un opérateur est $0,926$.
$\begin{align*} p_{\overline{A}}(M)&=\dfrac{p\left(\overline{A}\cap M\right)} {p\left(\overline{A}\right)} \\
&=\dfrac{0,3\times 0,13}{0,074}\\
&\approx 0,527
\end{align*}$
et
$\begin{align*} p_{\overline{A}}(I)&=\dfrac{p\left(\overline{A}\cap I\right)} {p\left(\overline{A}\right)} \\
&=\dfrac{0,7\times 0,05}{0,074}\\
&\approx 0,473
\end{align*}$
On constate donc que $p_{\overline{A}}(M) > p_{\overline{A}}(I)$.
Il est donc plus probable que ce soit un client mobile.
$\quad$
Partie C - Enquête de satisfaction
On a $n=1~303 \geqslant 30$ et $p=0,85$ donc $np=1~107,55\geqslant 5$ et $n(1-p)=195,45\geqslant 5$
Un intervalle de fluctuation asymptotique au niveau de confiance de $95\%$ est :
$\begin{align*} I_{1~303}&=\left[0,85-1,96\sqrt{\dfrac{0,85\times 0,15}{1~303}};0,85+1,96\sqrt{\dfrac{0,85\times 0,15}{1~303}}\right] \\
&\approx [0,830;0,869]
\end{align*}$
La fréquence observée est $f=\dfrac{1~150}{1~303} \notin I_{1~303}$.
Cela remet en cause l’annonce de la société au risque de $5\%$.
Le taux de satisfaction de l’échantillon est cependant supérieur à celui annoncé par la société.
$\quad$
- Vues: 22231
