Baccalauréat S Amérique du Nord 28 mai 2019 - Exercice 4
Page 7 sur 10
Exercice 4 5 points
On relie les centres de chaque face d'un cube ABCDEFGH pour former un solide IJKLMN comme sur la figure ci-dessous. 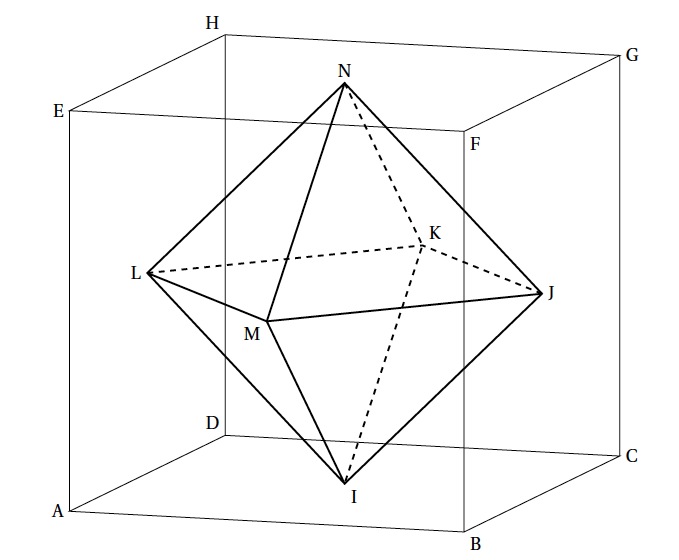
Plus précisément, les points I, J, K, L, M et N sont les centres respectifs des faces carrées ABCD, BCGF, CDHG, ADHE, ABFE et EFGH (donc les milieux des diagonales de ces carrés).
- Sans utiliser de repère (et donc de coordonnées) dans le raisonnement mené, justifier que les droites (IN) et (ML) sont orthogonales.
-
- Donner les coordonnées des vecteurs $ \vec{\text{NC}} $ et $ \vec{\text{ML}} $.
- En déduire que les droites (NC) et (ML) sont orthogonales.
- Déduire des questions précédentes une équation cartésienne du plan (NCI).
-
- Montrer qu'une équation cartésienne du plan (NJM) est : $x - y + z = 1 $.
- La droite (DF) est-elle perpendiculaire au plan (NJM)? Justifier.
- Montrer que l'intersection des plans (NJM) et (NCI) est une droite dont on donnera un point et un vecteur directeur. Nommer la droite ainsi obtenue en utilisant deux points de la figure.
Dans la suite, on considère le repère orthonormé $\left(\text{A}~;~\vec{\text{AB}}~;~\vec{\text{AD}}~;~\vec{\text{AE}}\right) $ dans lequel, par exemple, le point N a pour coordonnées $\left(\dfrac{1}{2}~;~\dfrac{1}{2}~;~1\right) $.
- Vues: 61066
