Baccalauréat S Métropole 20 juin 2013 - Correction Exercice 2
Page 4 sur 10
Correction de l'exercice 2 (7 points)
Sur le graphique ci-dessous, on a tracé , dans le plan muni d'un repère orthonormé $\left(\text{O},~\vec{i},\vec{j}\right)$, la courbe représentative $ \mathcal{C}$ d'une fonction $f$ définie et dérivable sur l'intervalle $]0;+\infty[$.
On dispose des informations suivantes:
- Les points $A, B, C$ ont pour coordonnées respectives (1, 0), (1, 2), (0, 2);
- la courbe $ \mathcal{C}$ passe par le point $B$ et la droite $(BC)$ est tangente à $ \mathcal{C}$ en $B$;
- il existe deux réels positifs $a$ et $b$ tels que pour tout réel strictement positif $x$, $f(x)=\dfrac{a+b\ln x }{x}$
-
- En utilisant le graphique, donner les valeurs de $f(1)$ et $f'(1)$.
Le point $B(1,2)$ est un point de $ \mathcal{C}$, donc $f(1)=2$
La tangente à $ \mathcal{C}$ au point $B$ d'abscisse 1 est horizontale , donc $f'(1)=0$.
$f(1)=2$ et $f'(1)=0$. - Vérifier que pour tout réel strictement positif $x, f'(x)=\dfrac{(b-a)-b\ln x }{x^2} $
$f=\dfrac{u}{v}$, donc $f'=\dfrac{u'v-v'u}{v^2}$
ici $u(x)=a+b\ln x$ et $v(x)=x$
on a donc $u'(x)=\dfrac{b}{x}$ et $v'(x)=1$
puis $f'(x)=\dfrac{\dfrac{b}{x}\times x -1\times \left (a+b\ln x\right )}{x^2}=\dfrac{b-a-b\ln x }{x^2} $
$f'(x)=\dfrac{(b-a)-b\ln x }{x^2} $. - En déduire les réels $a$ et $b$.
$f(1)=2 $ donc $\dfrac{a+b \ln 1}{1}=2$ donc $ a=2$, en effet $\ln 1=0$.
$f'(1)=0$ donc $ \dfrac{(b-a)-b\ln 1 }{1^2}=0 $ donc $ b-a=0 $ donc $ b=a=2$
$a=2$ et $b=2$ ainsi $f(x)=\dfrac{2+2\ln x }{x}$
- En utilisant le graphique, donner les valeurs de $f(1)$ et $f'(1)$.
-
- Justifier que pour tout réel $x$ appartenant à l'intervalle $]0;+\infty[$ , $f'(x)$ a le même signe que $-\ln x $.
D'après la question 1. $f'(x)=\dfrac{(b-a)-b\ln x }{x^2} =\dfrac{-2 \ln x }{x^2}$, on a remplacé $a$ et $b$ par 2.
Comme on travaille sur $]0;+\infty[$, on a $x^2>0$ et 2>0 ,
donc $f'(x)$ a le signe de $-\ln x$. - Déterminer les limites de $f$ en 0 et en $+\infty$.
On pourra remarquer que pour tout réel $x$ strictement positif, $f(x)=\dfrac{2}{x} +\dfrac{2\ln x}{x}$
- Limite en $0^+$ : sur $]0;+\infty[;f(x)=\dfrac{2+2\ln x }{x}=\left (2+2\ln x\right )\times \dfrac{ 1}{x}$
$\left.\begin{array}{l} \lim\limits_{x \to 0^+} (2+2\ln x)=-\infty\\ \lim\limits_{x \to 0^+}~\dfrac{1}{x}=+\infty \end{array}\right\}$ par produit on obtient: $\lim\limits_{x \to 0^+}~f(x)=-\infty$ - Limite en $+\infty$ : sur $]0;+\infty[;f(x)=\dfrac{2+2\ln x }{x}=\dfrac{2}{x} +\dfrac{2\ln x}{x}$
$\left.\begin{array}{l} \lim\limits_{x \to +\infty}~\dfrac{2}{x}=0\\ \lim\limits_{x \to +\infty}~\dfrac{2\ln x}{x}=0 \end{array}\right\}$ par somme on obtient: $\lim\limits_{x \to +\infty}~f(x)=0$
On a utilisé la limite de référence :$\lim\limits_{x \to +\infty}~\dfrac{ \ln x}{x}=0$
$\lim\limits_{x \to +\infty}~f(x)=0$
- Limite en $0^+$ : sur $]0;+\infty[;f(x)=\dfrac{2+2\ln x }{x}=\left (2+2\ln x\right )\times \dfrac{ 1}{x}$
- En déduire le tableau de variation de la fonction $f$. On sait que la dérivée a le signe de $-\ln x $ sur $]0;+\infty[$.
$f'(x)>0 \Leftrightarrow -\ln x > 0 \Leftrightarrow \ln x < 0 \Leftrightarrow0< x<1.$
$f'(x)=0 \Leftrightarrow x=1.$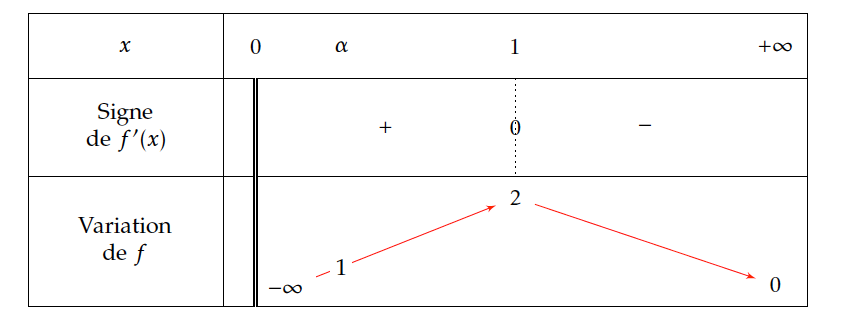
- Justifier que pour tout réel $x$ appartenant à l'intervalle $]0;+\infty[$ , $f'(x)$ a le même signe que $-\ln x $.
-
- Démontrer que l'équation $f(x)=1$ admet une unique solution $\alpha$ sur l'intervalle $]0,1]$.
$\left.\begin{array}{ll} &\bullet \quad f \text{ est continue sur } I=]0;1] \text{ (elle est dérivable sur )} I ;\\ &\bullet \quad f \text{ est strictement croissante sur } I ;\\ &\bullet \quad f(1)=2 ;\\ &\bullet \quad \lim\limits_{x \to 0^+} f(x)=-\infty.\\\end{array}\right\}$ . Comme $1 \in ]-\infty;2]$ l'équation $f(x)=1$ admet une unique solution $\alpha$ dans $I$
Ainsi l'équation $f(x)=1$ admet une unique solution $\alpha$ dans $I$ - Par un raisonnement analogue, on démontre qu'il existe un unique réel $\beta$ de l'intervalle $]1;+\infty[$ tel que $f(\beta )=1$.
Déterminer l'entier $n$ tel que $n< \beta<n+ 1$
soit $f(5)>f(\beta)>f(6)$
comme $f$ est strictement décroissante sur $[1;+\infty[$; on déduit $5<\beta< 6$
$5<\beta< 6$
- Démontrer que l'équation $f(x)=1$ admet une unique solution $\alpha$ sur l'intervalle $]0,1]$.
- On donne l'algorithme ci-dessous.
$$\begin{array}{|l l|}\hline \text{Variables : }& a, b \text{ et } m \text{ sont des nombres réels.}\\ \text{Initialisation :}& \text{Affecter à } a \text{ la valeur 0. } \\ & \text{ Affecter à } b \text{ la valeur 1. }\\ \text{Traitement :}& \text{ Tant que } b - a > 0,1\\ &\begin{array}{l|l} &\text{ Affecter à } m \text{ la valeur } \dfrac{1}{2}(a + b).\\ & \text{ Si } f(m) < 1 \text{ alors Affecter à } a \text{ la valeur } m.\\ & \text{Sinon Affecter à } b \text{ la valeur } m.\\ &F \text{ Fin de Si.}\\ \end{array}\\ &\text{ Fin de Tant que.}\\ \text{ Sortie : }& \text{ Afficher } a.\\ & \text{ Afficher } b.\\ \hline \end{array} $$- Faire tourner l'algorithme en complétant le tableau ci-dessous que l'on recopiera sur la copie.
$$\begin{array}{|c|c|c|c|c|c|} \hline &\text{ étape 1 } & \text{ étape 2 } &\text{ étape 3 } &\text{ étape 4 } & \text{ étape 5 } \\ \hline a & 0 & 0 & 0,25 & 0,375 & 0,4375 \\ \hline b & 1 & 0,5 & 0,5 & 0,5 & 0,5 \\ \hline b-a & 1 & 0,5 & 0,25 &0,125 & 0,0625\\ \hline m & 0,5 & 0,25 & 0,375 & 0,4375 & \text{ L'algorithme s'arrête car la condition } b-a\leq 0,1 \text{est réalisée }\\ \hline \end{array}$$ - Que représentent les valeurs affichées par cet algorithme?
Cet algorithme fournit un encadrement à 0,1 près de l'unique solution $\alpha$ de l'équation $f(x)=1$ se trouvant dans l'intervalle $]0,1]$. La méthode utilisée est la dichotomie. - Modifier l'algorithme ci-dessus pour qu'il affiche les deux bornes d'un encadrement de $\beta$ d'amplitude $10^{-1}$.
$$\begin{array}{|l l|}\hline \text{Variables : }& a, b \text{ et } m \text{ sont des nombres réels.}\\ \text{Initialisation :}& \text{Affecter à } a \text{ la valeur 5. } \\ & \text{ Affecter à } b \text{ la valeur 6. }\\ \text{Traitement :}& \text{ Tant que } b - a > 0,1\\ &\begin{array}{l|l} &\text{ Affecter à } m \text{ la valeur } \dfrac{1}{2}(a + b).\\ & \text{ Si } f(m) < 1 \text{ alors Affecter à } a \text{ la valeur } m.\\ & \text{Sinon Affecter à } b \text{ la valeur } m.\\ &F \text{ Fin de Si.}\\ \end{array}\\ &\text{ Fin de Tant que.}\\ \text{ Sortie : }& \text{ Afficher } a.\\ & \text{ Afficher } b.\\ \hline \end{array} $$
- Faire tourner l'algorithme en complétant le tableau ci-dessous que l'on recopiera sur la copie.
- Le but de cette question est de démontrer que la courbe $ \mathcal{C}$ partage le rectangle $OABC$ en deux domaines d'aires égales.
- Justifier que cela revient à démontrer que $\displaystyle\int_{\dfrac{1}{e}}^{1}f(x)\;dx=1$.
Le rectangle $OABC$ a pour aire $\mathcal{A}=OA \times BC =2 (u.a.)$
On résout l'équation $f(x)=0$ sur $]0;+\infty[$
$f(x)=0 \Leftrightarrow \dfrac{2+2\ln x }{x} \Leftrightarrow 2+2\ln x =0 \Leftrightarrow \ln x =-1 \Leftrightarrow x=e^{-1} \Leftrightarrow x=\dfrac{1}{e}$.
La courbe $ \mathcal{C}$ rencontre l'axe des abscisses au point d'abscisse $x=\dfrac{1}{e}$.
On doit donc montrer que l'aire du domaine délimité par la courbe $ \mathcal{C}$ , l'axe des abscisses et les droites d'équation $x=\dfrac{1}{e}$ et $x=1$ vaut $1 u.a.$.
Comme $f$ est continue, positive sur $\left [\dfrac{1}{e};1\right ]$, en effet :
si $x\geq \dfrac{1}{e}$ alors $\ln x\geq \ln\left (\dfrac{1}{e}\right )$
soit $1+\ln x\geq 0$ puis en multipliant par $\dfrac{2}{x}>0$ sur $]0;++\infty[$, on obtient $f(x)\geq 0$,
cette aire vaut $\mathcal{B}= \int_{\dfrac{1}{e}}^{1}f(x)\;dx$.
On doit donc établir $\mathcal{B}=1$ soit $\displaystyle\int_{\dfrac{1}{e}}^{1}f(x)\;dx=1$. - En remarquant que l'expression de $f(x)$ peut s'écrire $\dfrac{2}{x} +2\times \dfrac{1}{x}\times \ln x $, terminer la démonstration.
$f(x)=\dfrac{2}{x} +2\times \dfrac{1}{x}\times \ln x =2\times \dfrac{1}{x}+2 u'(x)\times u(x)$ où $u(x)=\ln x$ .
On note $F$ une primitive de $f$ sur $]0;+\infty[$.
$F(x)=2\ln x +\left (\ln x \right )^2$. On a utilisé le fait que $u'u^n$ a pour primitive $\dfrac{u^{n+1}}{n+1}$ pour $n\neq -1$.
$$\int_{\dfrac{1}{e}}^{1}f(x)\;dx=F(1)-F\left (\dfrac{1}{e}\right )=2\ln 1 +\left (\ln 1 \right )^2 -\left (2\ln\left (\dfrac{1}{e}\right )+\left (\ln \left (\dfrac{1}{e}\right )\right )^2\right ) =0-(-2+1)=1$$ En effet $\ln\left (\dfrac{1}{e}\right )=-\ln e=-1$
- Justifier que cela revient à démontrer que $\displaystyle\int_{\dfrac{1}{e}}^{1}f(x)\;dx=1$.
- Vues: 45448
