Baccalauréat S Polynésie 19 juin 2019 - Exercice 2
Exercice 2 5 points
L'écoulement de l'eau d'un robinet a un débit constant et modéré. 
On s'intéresse en particulier à une partie du profil d'écoulement représentée en annexe 1 par la courbe $C$ dans un repère orthonormé.
Partie A
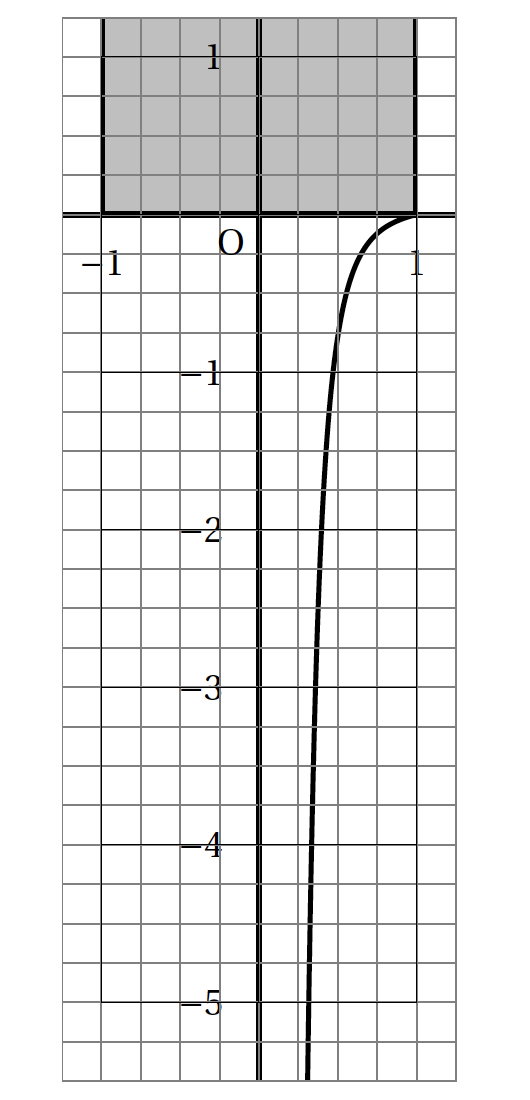
On considère que la courbe $C$ donnée en annexe 1 est la représentation graphique d'une fonction $f$ dérivable sur l'intervalle ]0 ; 1] qui respecte les trois conditions suivantes: \[(H):\: f(1) = 0\qquad f'(1) = 0,25\quad \text{et} \:\: \displaystyle\lim_{\substack{x \to 0\\x > 0}} f(x) = - \infty.\]
- La fonction $f$ peut-elle être une fonction polynôme du second degré ? Pourquoi ?
- Soit $g$ la fonction définie sur l'intervalle ]0 ; 1] par $g(x) = k \ln x$.
- Déterminer le réel $k$ pour que la fonction $g$ respecte les trois conditions $(H)$.
- La courbe représentative de la fonction $g$ coïncide-t-elle avec la courbe $C$ ? Pourquoi ?
- Soit $h$ la fonction définie sur l'intervalle ]0 ; 1] par $h(x) = \dfrac{a}{x^4} + bx$ où $a$ et $b$ sont des réels. Déterminer $a$ et $b$ pour que la fonction $h$ respecte les trois conditions $(H)$.
Partie B
On admet dans cette partie que la courbe $C$ est la représentation graphique d'une fonction $f$continue, strictement croissante, définie et dérivable sur l'intervalle ]0 ; 1] d'expression: \[f(x) = \dfrac{1}{20}\left(x - \dfrac{1}{x^4} \right).\]
- Justifier que l'équation $f(x) = -5$ admet sur l'intervalle ]0 ; 1] une unique solution qui sera notée $\alpha$. Déterminer une valeur approchée de $\alpha$ à $10^{-2}$ près.
- On admet que le volume d'eau en cm$^3$, contenu dans les 5 premiers centimètres de l'écoulement, est donné par la formule : $$V = \displaystyle\int_{\alpha}^1\pi x^2 f'(x)\:\text{d}x.$$
- Soit $u$ la fonction dérivable sur ]0 ; 1] définie par $u(x) = \dfrac{1}{2x^2}$. Déterminer sa fonction dérivée.
- Déterminer la valeur exacte de $V$. En utilisant la valeur approchée de $\alpha$ obtenue à la question 1, donner alors une valeur approchée de $V$.
Annexe 1
- Vues: 46365
