Baccalauréat S Polynésie 19 juin 2019 - Correction Exercice 2
Correction de l'exercice 2 (5 points)
L'écoulement de l'eau d'un robinet a un débit constant et modéré. 
On s'intéresse en particulier à une partie du profil d'écoulement représentée en annexe 1 par la courbe $C$ dans un repère orthonormé.
Partie A
On considère que la courbe $C$ donnée en annexe 1 est la représentation graphique d'une fonction $f$ dérivable sur l'intervalle ]0 ; 1] qui respecte les trois conditions suivantes: \[(H):\: f(1) = 0\qquad f'(1) = 0,25\quad \text{et} \:\: \displaystyle\lim_{\substack{x \to 0\\x > 0}} f(x) = - \infty.\]
- La fonction $f$ peut-elle être une fonction polynôme du second degré ? Pourquoi ? Si une expression algébrique de $f$ est, sur l’intervalle $]0;1]$, $f(x)=ax^2+bx+c$ alors $\lim\limits_{x \to 0^+}=c$
- Soit $g$ la fonction définie sur l'intervalle ]0 ; 1] par $g(x) = k \ln x$.
- Déterminer le réel $k$ pour que la fonction $g$ respecte les trois conditions $(H)$. La fonction $g$ est dérivable sur l’intervalle $]0;1]$ en tant que produit d’une fonction dérivable sur cet intervalle par un réel.
- La courbe représentative de la fonction $g$ coïncide-t-elle avec la courbe $C$ ? Pourquoi ? On a $f(0,3)\approx -5,5$ et $g(0,3)\approx -0,30$.
Ainsi, pour tout réel $x\in]0;1]$ on a : $g'(x)=\dfrac{k}{x}$.
Par conséquent $g'(1)=k$.
Si la fonction $g$ vérifie les trois conditions (H) on a donc $g'(1)=0,25$ et donc $k=0,25$.
Ainsi $g(x)=0,25\ln x$.
De plus $g(1)=0,25\ln 1=0$
Et, puisque $\lim\limits_{x \to 0^+} \ln x=-\infty$ et que $0,25>0$, on a$\lim\limits_{x \to 0^+}g(x)=-\infty$.
$\quad$
La courbe représentative de la fonction $g$ ne coïncide donc pas avec la courbe $C$.
$\quad$ - Soit $h$ la fonction définie sur l'intervalle ]0 ; 1] par $h(x) = \dfrac{a}{x^4} + bx$ où $a$ et $b$ sont des réels. Déterminer $a$ et $b$ pour que la fonction $h$ respecte les trois conditions $(H)$. On a $h(1)=a+b=0 \iff a=-b$.
D’après l’énoncé on a $\lim\limits_{x\to 0^+}=-\infty$.
La fonction $f$ ne donc pas une fonction polynôme du second degré.
$\quad$
La fonction $h$ est dérivable sur l’intervalle $]0;1]$ en tant que somme de fonctions dérivables sur cet intervalle.
Ainsi, pour tout réel $x\in]0;1]$ on a $h'(x)=-\dfrac{4a}{x^5}+b$.
Or $h'(1)=0,25 \iff -4a+b=0,25$.
On doit donc résoudre le système :
$\begin{align*} \begin{cases}a=-b\\-4a+b=0,25\end{cases} &\iff \begin{cases} a=-b\\4b+b=0,25\end{cases}\\
&\iff \begin{cases} a=-b\\5b=0,25 \end{cases}\\
&\iff \begin{cases} b=0,05\\a=-0,05\end{cases}\end{align*}$
Ainsi $h(x)=0,05x-\dfrac{0,05}{x^4}$.
Vérifions que les trois conditions sont bien vérifiées :
$h(1)=0,05-0,05=0$.
$h'(1)=0,05+\dfrac{4\times 0,05}{1^5}=0,25$.
$\lim\limits_{x\to 0^+} h(x)=\lim\limits_{x\to 0^+}-\dfrac{0,05}{x^4}=-\infty$.
$\quad$
Partie B
On admet dans cette partie que la courbe $C$ est la représentation graphique d'une fonction $f$continue, strictement croissante, définie et dérivable sur l'intervalle ]0 ; 1] d'expression: \[f(x) = \dfrac{1}{20}\left(x - \dfrac{1}{x^4} \right).\]
- Justifier que l'équation $f(x) = -5$ admet sur l'intervalle ]0 ; 1] une unique solution qui sera notée $\alpha$. Déterminer une valeur approchée de $\alpha$ à $10^{-2}$ près. On a $f(x)=\dfrac{1}{20}\left(x-\dfrac{1}{x^4}\right)$ sur l’intervalle $]0;1]$.
- On admet que le volume d'eau en cm$^3$, contenu dans les 5 premiers centimètres de l'écoulement, est donné par la formule : $$V = \displaystyle\int_{\alpha}^1\pi x^2 f'(x)\:\text{d}x.$$
- Soit $u$ la fonction dérivable sur ]0 ; 1] définie par $u(x) = \dfrac{1}{2x^2}$. Déterminer sa fonction dérivée. Sur l’intervalle $]0;1]$ on a $u'(x)=\dfrac{1}{2}\times \dfrac{-2}{x^3}=-\dfrac{1}{x^3}$.
- Déterminer la valeur exacte de $V$. En utilisant la valeur approchée de $\alpha$ obtenue à la question 1, donner alors une valeur approchée de $V$. On a :
$\quad$
$\begin{align*} \displaystyle V&=\int_{\alpha}^1 \pi x^2 f'(x)\text{d} x \\
&=\pi \int_{\alpha}^1 \left(\dfrac{1}{20}\left(1+\dfrac{4}{x^5}\right)\right)\times x^2\text{d} x \\
&=\dfrac{\pi}{20}\int_{\alpha}^1 \left(x^2+\dfrac{4}{x^3}\right)\text{d} x \\
&=\dfrac{\pi}{20}\left[\dfrac{x^3}{3}-4\times \dfrac{1}{2x^2}\right]_{\alpha}^1 \\
&=\dfrac{\pi}{20}\left(\dfrac{1}{3}-2-\left(\dfrac{\alpha^3}{3}-\dfrac{2}{\alpha^2}\right)\right) \\
&=\dfrac{\pi}{20}\left(-\dfrac{5}{3}-\dfrac{\alpha^3}{3}+\dfrac{2}{\alpha^2}\right)\\
&\approx 2,8 \text{ cm}^3\end{align*}$.
$\quad$
Ainsi $f'(x)=\dfrac{1}{20}\left(1+\dfrac{4}{x^5}\right)$.
Par conséquent, $f'(x)>0$ sur l’intervalle $]0;1]$ en tant que somme de fonctions positives sur cet intervalle.
La fonction $f$ est donc continue et strictement croissante sur l’intervalle $]0;1]$.
$\lim\limits_{x \to 0^+} f(x)=-\infty$ et $f(1)=0$.
Or $-5\in]-\infty;0]$.
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) l’équation $f(x)=-5$ possède une unique solution $\alpha$ sur l’intervalle $]0;1]$.
D’après la calculatrice $\alpha\approx 0,32$.
$\quad$
Annexe 1
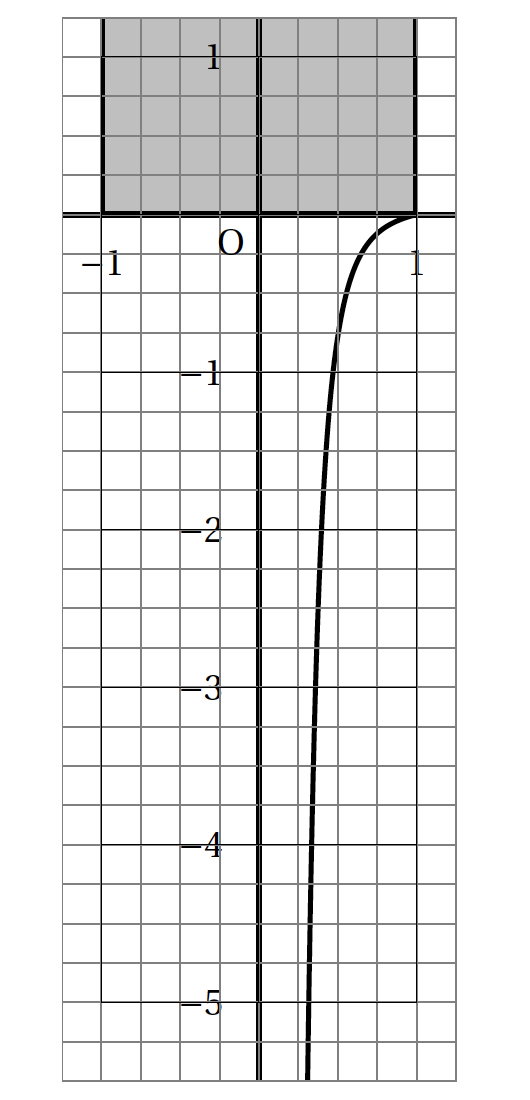
- Vues: 46364
