Baccalauréat STI2D Métropole - La Réunion - 19 juin 2018 - Exercice 3

Page 5 sur 8: Exercice 3

Exercice 3 6 points

Fonctions

Le niveau sonore $N$ d’un bruit, à une distance $D$ de sa source, dépend de la puissance sonore $P$ de la source. Il est donné par la relation $$ N =120+4\ln\left(\dfrac{P}{13D^2}\right)$$ où $N$ est exprimé en décibels (dB), $P$ en Watts (W) et $D$ en mètres (m).

Partie A

Les questions 1. et 2. sont indépendantes.

1. Calculer le niveau sonore $N$ d’un bruit entendu à 10 mètres de la source sonore dont la puissance $P$ est égale à 2,6 Watts. On arrondira le résultat à l’unité.
2. On donne $N = 84$ dB et $D = 10$ m. Déterminer $P$. On arrondira le résultat à $10^{-2}$ près.

Partie B

Une entreprise de travaux publics réalise un parking en plein air. Sur le chantier d’aménagement de ce parking, une machine de découpe a une puissance sonore $P$ égale à 0,026 Watts.

1. 1. Montrer qu'à une distance $D$ de la machine, le niveau sonore $N$ dû à celle-ci vérifie la relation : $$N= 120 + 4\ln(0,002)-4\ln(D^2)$$
   2. Montrer qu’une approximation de $N$ peut être $95,14 - 8\ln(D)$.
      Dans la suite de l’exercice, à une distance de $x$ mètres de la machine, le niveau sonore $N$ émis par la machine est modélisé par la fonction $f$ définie sur l’intervalle $[0,1 ; 20]$ par : $$f(x) = 95,14 - 8 \ln(x)$$
2. 1. Déterminer une expression de $f'(x)$, où $f$ désigne la fonction dérivée de $f$.
   2. Donner le signe de $f'(x)$ pour tout $x$ de l'intervalle $[0,1 ; 20]$.
   3. En déduire le sens de variation de la fonction $f$ sur l’intervalle $[0,1 ; 20]$.
3. On suppose qu’un ouvrier de cette entreprise se situe à trois mètres de la machine. La législation en vigueur l’oblige à porter des protections individuelles contre le bruit dès qu’un risque apparaît. Justifier, à l’aide du tableau ci-dessous, que l’ouvrier doit porter des protections individuelles contre le bruit. $$\begin{array}{|c|c|} \hline \textbf{Impacts sur l'audition}& \textbf{Niveaux sonores en décibels} \\ \hline \text{Aucun}& [0;85[\\ \hline \text{ Risque faible } &[85; 90[ \\ \hline \text{ Risque élevé } & [90; 120[\\ \hline \end{array}$$
4. Déterminer à quelle distance de la machine un ouvrier de l'entreprise sort de la zone de risque élevé ( c'est-à-dire lorsque le niveau sonore est inférieur à 90 dB).

Partie C

On s’intéresse au lien entre la puissance $P$ d’un bruit et la distance $D$ de sa source pour différentes valeurs de son niveau sonore $N$.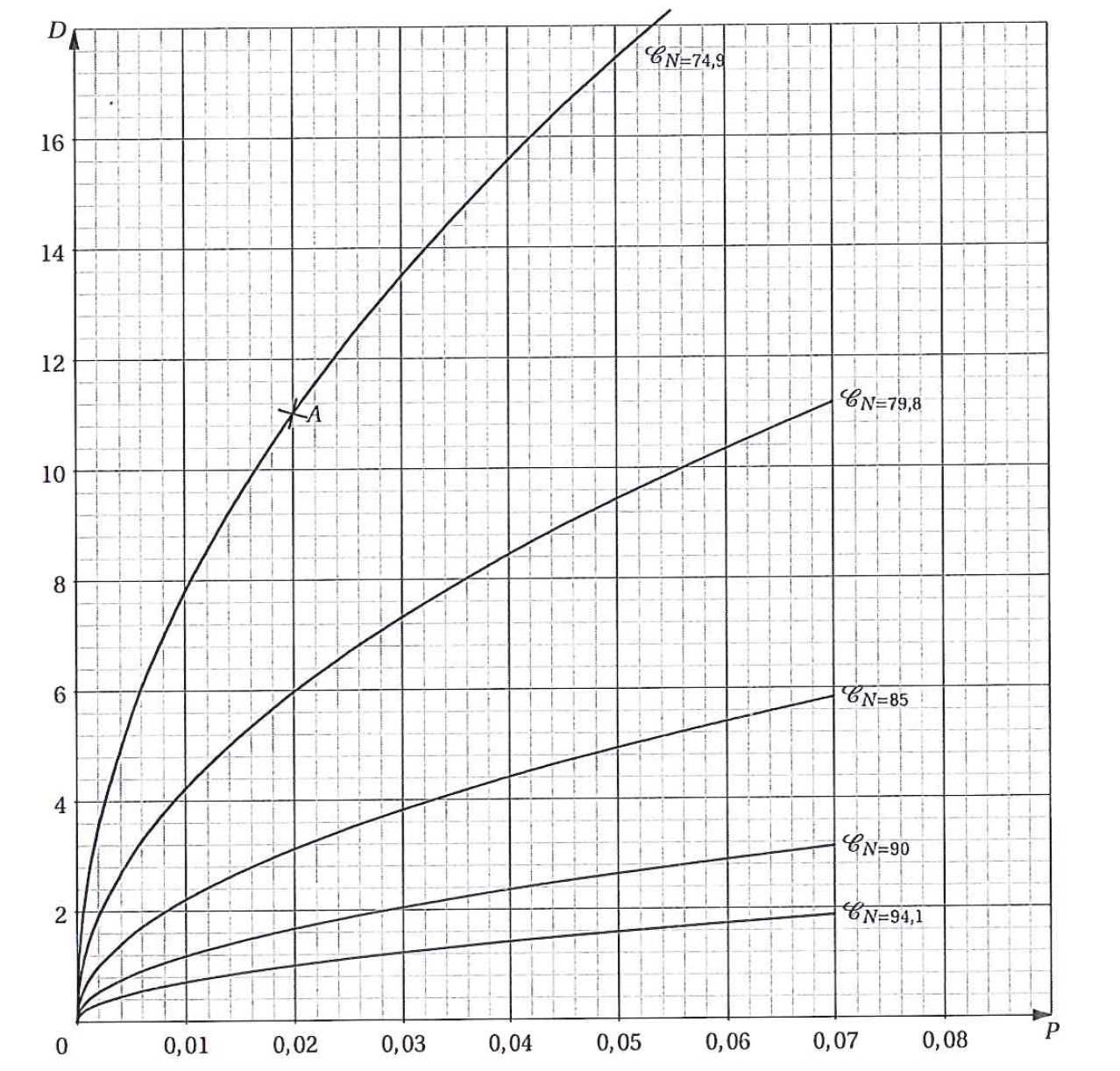

On admet que pour une puissance de 0,02 Watt, le niveau sonore du bruit est de 74,9 décibels à une distance de 11 mètres de la source sonore. Ainsi, le point A de coordonnées (0,02; 11) appartient à la courbe $\mathcal{C}_N=74,9$.

1. Pour un bruit de puissance $P$ égale à 0,06 W, déterminer graphiquement à quelles distances minimale et maximale de la source peut se situer une personne pour que le niveau sonore $N$ soit compris entre 85 et 90 dB.
2. Pour une source sonore située à une distance $D$ de 8 m, déterminer graphiquement les puissances minimale et maximale de cette source pour obtenir un niveau sonore compris entre 74,9 dB et 79,8 dB.