Baccalauréat S Pondichéry 17 avril 2015
Page 1 sur 10
Exercice 1 4 points
Partie A
Soit $f$ la fonction définie sur $\mathbb R$ par \[f(x) = \dfrac{3}{1 + \text{e}^{- 2x}}.\] Sur le graphique ci-après, on a tracé, dans un repère orthogonal $\left(\text{O},~\vec{i},~\vec{j}\right)$, la courbe représentative $\mathcal{C}$ de la fonction $f$ et la droite $\Delta$ d'équation $y = 3$. 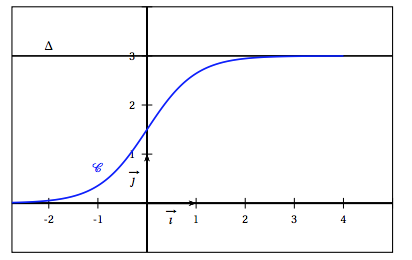
- Démontrer que la fonction $f$ est strictement croissante sur $\mathbb R$.
- Justifier que la droite $\Delta$ est asymptote à la courbe $\mathcal{C}$.
- Démontrer que l'équation $f(x) = 2,999$ admet une unique solution $\alpha$ sur $\mathbb R$. Déterminer un encadrement de $\alpha$ d'amplitude $10^{-2}$.
Partie B
Soit $h$ la fonction définie sur $\mathbb R$ par $h(x) = 3 - f(x)$.
- Justifier que la fonction $h$ est positive sur $\mathbb R$.
- On désigne par $H$ la fonction définie sur $\mathbb R$ par $H(x) = - \dfrac{3}{2} \ln \left(1 + \text{e}^{- 2x}\right)$. Démontrer que $H$ est une primitive de $h$ sur $\mathbb R$.
- Soit $a$ un réel strictement positif.
- Donner une interprétation graphique de l'intégrale $\displaystyle\int_0^a h(x)\:\text{d}x$.
- Démontrer que $\displaystyle\int_0^a h(x)\:\text{d}x = \dfrac{3}{2} \ln \left(\dfrac{2}{1 + \text{e}^{- 2a}}\right)$.
- On note $\mathcal{D}$ l'ensemble des points $M(x~;~y)$ du plan défini par $\left\{\begin{array}{l c l} x&\geqslant & 0\\ f(x) &\leqslant y&\leqslant 3 \end{array}\right.$
Déterminer l'aire, en unité d'aire, du domaine $\mathcal{D}$.
- Vues: 32222
