Baccalauréat S Pondichéry 17 avril 2015 - Correction Exercice 3

Page 6 sur 10: Correction Exercice 3

Correction de l'exercice 3 (5 points)

Commun à tous les candidats

ProbabilitésLes parties A et B peuvent être traitées indépendamment .
Partie A Etude de la durée de vie d'un appareil électroménager
Des études statistiques ont permis de modéliser la durée de vie, en mois, d'un type de lave-vaisselle par une variable aléatoire $X$ suivant une loi normale $\mathcal{N}\left(\mu,~ \sigma^2\right)$ de moyenne $\mu = 84$ et d'écart-type $\sigma$. De plus, on a $P(X \leqslant 64) = 0,16$. La représentation graphique de la fonction densité de probabilité de $X$ est donnée ci-dessous.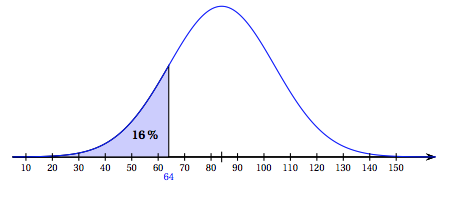

1. 1. En exploitant le graphique, déterminer $P(64 \leqslant X \leqslant 104)$.
   On a $P(X \le \mu -20) = 0,16$ donc $P(X \ge \mu + 20) = P(X \ge 104)= 0,16$.
   Or $P(X \le 64) + P(64 \le X \le 104) + P(X \ge 104) = 1$
   Par conséquent $P(64 \le X \le 104) = 1 – 2 \times 0,16 = 0,68)$.
   
   2. Quelle valeur approchée entière de $\sigma$ peut-on proposer ?
   On a ainsi $P(\mu – 20 \le X \le \mu +20) = 0,68$.
   D’après le résultat du cours, cela signifie que $\sigma \approx 20$.
2. On note $Z$ la variable aléatoire définie par $Z = \dfrac{X - 84}{\sigma}$.
   1. Quelle est la loi de probabilité suivie par $Z$ ?
   La variable aléatoire $Z$ suit la loi normale centrée réduite.
   
   2. Justifier que $P(X \leqslant 64) = P \left(Z \leqslant \dfrac{- 20}{\sigma}\right)$.
   
   $$\begin{array}{rl} P(X \le 64) & = P(X – 84 \le -20) \\ & = P\left( \dfrac{X – 84}{\sigma}\le \dfrac{-20}{\sigma}\right)\\ & = P \left(Z \le \dfrac{-20}{\sigma}\right) \end{array}$$
   3. En déduire la valeur de $\sigma$, arrondie à $10^{-3}$.
   On a donc $P \left(Z \le \dfrac{-20}{\sigma}\right) = 0,16$.
   Par conséquent $\dfrac{-20}{\sigma} \approx -0,9945$
   donc $\sigma \approx 20,11$.
   Remarque : $$\begin{array}{rl} P \left(Z \le \dfrac{-20}{\sigma}\right) = 0,16&\iff \pi\left(\dfrac{-20}{\sigma}\right) = 0,16\\ & \iff \dfrac{-20}{\sigma}= \pi^{-1}(0.16)\\ &\iff -20 = \sigma \pi^{-1}(0.16)\\ &\iff \sigma= \dfrac{-20}{\pi^{-1}(0.16)}\\ &\iff \sigma= -20\times Fracnormale(0.16) \end{array}$$

   2ND DISTR 3Fracnormale( $\1 $ )EXE
   Avec une calculatrice de type TI

   $$Fracnormale( \1 ) \approx \2$$

   $$\pi^{-1}( \1)\approx \2 \text{ à } 10^{-\3} \text{ près.}$$
3. Dans cette question, on considère que $\sigma = 20,1$. Les probabilités demandées seront arrondies à $10^{-3}$.
   1. Calculer la probabilité que la durée de vie du lave-vaisselle soit comprise entre 2 et 5 ans.
   On cherche donc $P(24 \le X \le 60) \approx 0,115$
   
   

   2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
   Avec une calculatrice de type TI

   $$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$

   $$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$

    

   
   
   
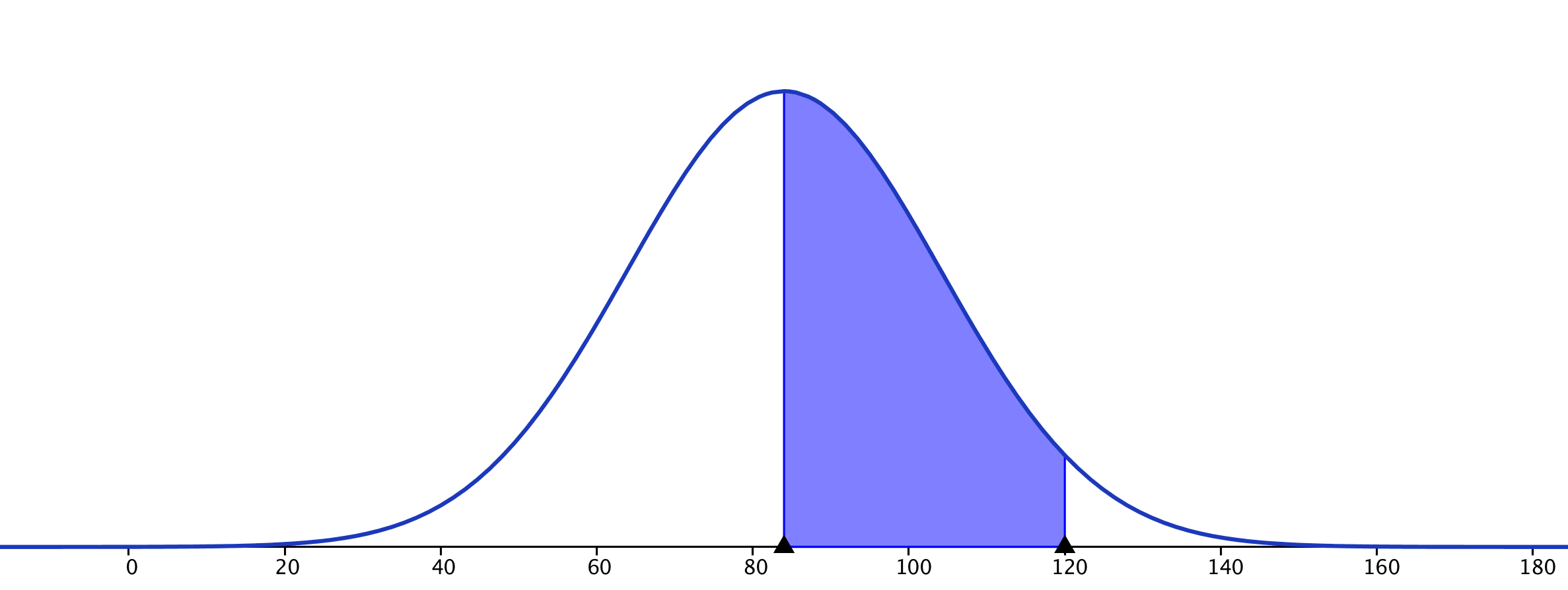
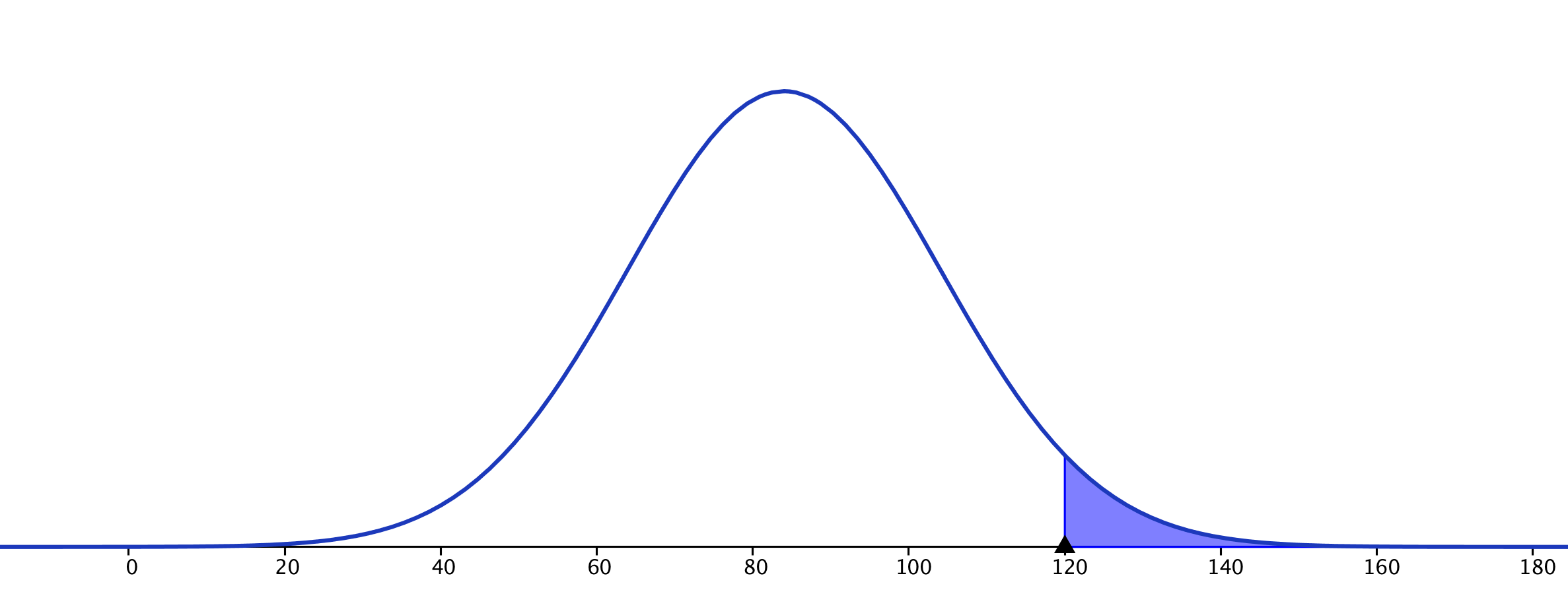
   2. Calculer la probabilité que le lave-vaisselle ait une durée de vie supérieure à 10 ans.
   $P(X \le 120) = 0,5 – P(84 \le X \le 120) \approx 0,037$

    

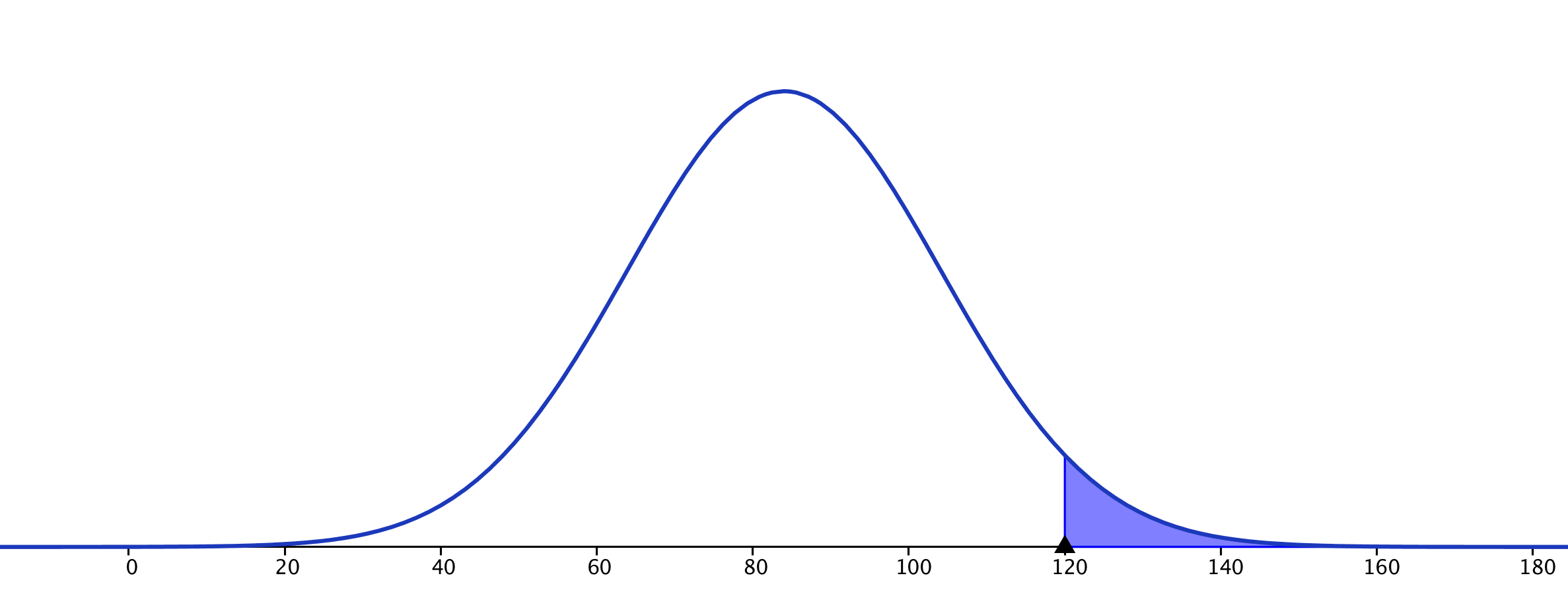
   2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
   Avec une calculatrice de type TI

   $$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$

   $$P( \5 \geq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$

Partie B Etude de l'extension de garantie d'El'Ectro
Le lave-vaisselle est garanti gratuitement pendant les deux premières années. L'entreprise El'Ectro propose à ses clients une extension de garantie de 3 ans supplémentaires. Des études statistiques menées sur les clients qui prennent l'extension de garantie montrent que 11,5 % d'entre eux font jouer l'extension de garantie.

1. On choisit au hasard 12 clients parmi ceux ayant pris l'extension de garantie (on peut assimiler ce choix à un tirage au hasard avec remise vu le grand nombre de clients).
   1. Quelle est la probabilité qu'exactement 3 de ces clients fassent jouer cette extension de garantie ? Détailler la démarche en précisant la loi de probabilité utilisée. Arrondir à $10^{-3}$.
   On appelle $C$ la variable aléatoire comptant le nombre de clients faisant jouer l’extension de garantie.
   

   On répète $\1$  fois, de façon indépendante, l’expérience «\2 » qui comporte 2 issues :

   • « \3 » considéré comme succès, de probabilité $p=\4$
   • « \5 » considéré comme échec, de probabilité $q=1-p=\6$

   Nous sommes donc en présence d’un schéma de Bernoulli et la variable aléatoire $\7$ prenant pour valeurs le nombre de succès obtenus suit la loi binomiale de paramètres $\1$  et $\4$ notée $\mathscr{B}(\1;\4)$ .

   Pour tout entier $k$ où $0\leq k\leq \1$, on a $$P(\7=k)=\binom{\1}{k}\times \left(\4\right)^k\times\left( \6\right)^{\1-k}$$

   2ND DISTR 0binomFdP( \1 , \2,\3)EXE
   Avec une calculatrice de type TI $binomFdP(\1,\2,\3) \approx \4$

   $$P( \5 = \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
   
   
   2. Quelle est la probabilité qu'au moins 6 de ces clients fassent jouer cette extension de garantie ? Arrondir à $10^{-3}$.
   On veut $P(C \ge 6) = 1 – P(C \le 5) \approx 0,001$. (résultat obtenu à l’aide de la calculatrice).
   

    

   2ND DISTR AbinomFRép( \1 , \2,\3)EXE
   Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$

   $$P( \5 \leq \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
2. L'offre d'extension de garantie est la suivante : pour 65 euros supplémentaires, El'Ectro remboursera au client la valeur initiale du lave-vaisselle, soit 399 euros, si une panne irréparable survient entre le début de la troisième année et la fin de la cinquième année . Le client ne peut pas faire jouer cette extension de garantie si la panne est réparable. On choisit au hasard un client parmi les clients ayant souscrit l'extension de garantie, et on note $Y$ la variable aléatoire qui représente le gain algébrique en euros réalisé sur ce client par l'entreprise El'Ectro, grâce à l'extension de garantie.
   1. Justifier que $Y$ prend les valeurs $65$ et $- 334$ puis donner la loi de probabilité de $Y$.
   Il y a deux possibilités :
   – le client ne fait pas jouer l’extension de garantie et auquel cas l’entreprise gagne $65$ euros.
   – le client fait jouer l’extension de garantie et l’entreprise perd $399 – 65 = 334$ euros.
   Ainsi $Y$ prend bien deux valeurs $65$ et $ -334$.
   
   2. Cette offre d'extension de garantie est-elle financièrement avantageuse pour l'entreprise ? Justifier.
   On a $P(Y = -334) = 0,115$ donc $P(Y = 65) = 0,885$.
   Ainsi $E(Y) = 0,115 \times (-334) + 65 \times 0,885 = 19,115 > 0$.
   Cette offre est donc financièrement avantageuse pour l’entreprise.